Toán 8 Bài 1 (Chân trời sáng tạo): Đơn thức và đa thức nhiều biến
Với giải bài tập Toán lớp 8 Bài 1: Đơn thức và đa thức nhiều biến sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 8 Bài 1.
Giải Toán 8 Bài 1: Đơn thức và đa thức nhiều biến
Bài giảng Toán 8 Bài 1: Đơn thức và đa thức nhiều biến - Chân trời sáng tạo
Thực hành 1 trang 7 Toán 8 Tập 1: Cho các biểu thức sau:
ab−πr2ab−πr2; 4πr334πr33; p2πp2π; x−1yx−1y; 00; 1√21√2; x3−x+1x3−x+1.
Trong các biểu thức trên, hãy chỉ ra:
b) Các đa thức và số hạng tử của chúng
Lời giải:
a) Các đơn thức là: 4πr334πr33; p2πp2π; 00; 1√21√2.
b) Các đa thức là: ab−πr2ab−πr2; x3−x+1x3−x+1.
Đa thức ab−πr2ab−πr2 có hai hạng tử.
Đa thức x3−x+1x3−x+1 có ba hạng tử
a) Viết biểu thức biểu thị diện tích bức tường (không tính phần cửa sổ).
Lời giải:
a) Diện tích bức tường (có tính cửa sổ) là: (a+2a).h2=3ah2=32ah(a+2a).h2=3ah2=32ah.
Diện tích cửa sổ là: r.r.3,14=3,14r2r.r.3,14=3,14r2
Biểu thức biểu thị diện tích bức tường (không tính cửa sổ) là: S=32ah−3,14r2S=32ah−3,14r2
b) Thay a=2a=2m; h=3mh=3m, r=0,5r=0,5m vào đa thức SS ta có:
S=32.2.3−3,14.0,52=9−0,785=8,215≈8,22S=32.2.3−3,14.0,52=9−0,785=8,215≈8,22
Lời giải:
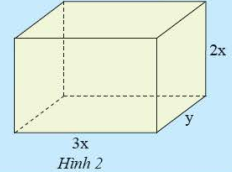
Ta có: V=3xy.2x=(3.2).(x.x).y=6x2yV=3xy.2x=(3.2).(x.x).y=6x2y
Kết quả của hai bạn An và Tâm là giống nhau.
Thực hành 2 trang 9 Toán 8 Tập 1: Thu gọn các đơn thức sau đây. Chỉ ra hệ số và bậc của chúng.
a) 12xy2x12xy2x b) −y(2z)y−y(2z)y
c) x3yxx3yx d) 5x2y3z4y5x2y3z4y
Lời giải:
a) Ta có: 12xy2x=12.(x.x).y2=12x2y212xy2x=12.(x.x).y2=12x2y2
Đơn thức trên có hệ số là 1212, bậc bằng 2+2=42+2=4.
b) Ta có: −y(2z)y=−2.(y.y).z=−2y2z−y(2z)y=−2.(y.y).z=−2y2z
Đơn thức trên có hệ số là −1−1, bậc bằng 2+1=32+1=3.
c) Ta có: x3yx=(x3.x).y=x4yx3yx=(x3.x).y=x4y
Đơn thức trên có hệ số là 11, bậc bằng 4+1=54+1=5.
d) Ta có: 5x2y3z4y=5x2.(y3.y).z4=5x2y4z45x2y3z4y=5x2.(y3.y).z4=5x2y4z4
Đơn thức trên có hệ số là 55, bậc bằng 2+4+4=102+4+4=10.
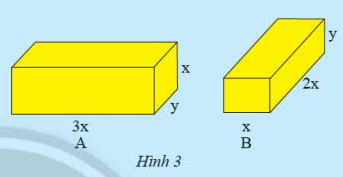
HĐ3 trang 9 Toán 8 Tập 1: Cho hai hình hộp chữ nhật A và B có các kích thước như hình 3.
a) Tính tổng thể tích của hình hộp chữ nhật A và B.
b) Viết biểu thức biểu diễn sự chênh lệch thể tích của A và B.
Lời giải:
a) Thể tích của hình hộp chữ nhật A là: VA=3x.y.x=3.x2yVA=3x.y.x=3.x2y
Thể tích của hình hộp chữ nhật B là: VB=2x.x.y=2x2yVB=2x.x.y=2x2y
Tổng thể tích của hình hộp chữ nhật A và B là: 3x2y+2x2y=(3+2).x2y=5x2y3x2y+2x2y=(3+2).x2y=5x2y
b) Biểu thức biểu diễn sự chênh lệch thể tích của A và B là: 3x2y−2x2y=(3−2).x2y=x2y3x2y−2x2y=(3−2).x2y=x2y
a) xyxy và −6xy−6xy b) 2xy2xy và xy2xy2
Lời giải:
a) xyxy và −6xy−6xy là hai đơn thức đồng dạng vì có hệ số khác 00 và có cùng phần biến là xyxy.
Ta có:
xy+(−6xy)=xy−6xy=(1−6)xy=−5xyxy+(−6xy)=xy−6xy=(1−6)xy=−5xy
xy−(−6xy)=xy+6xy=(1+6)xy=7xyxy−(−6xy)=xy+6xy=(1+6)xy=7xy
b) 2xy2xy và xy2xy2 không là hai đơn thức đồng dạng.
c) −4yzx2−4yzx2 và 4x2yz4x2yz là hai đơn thức đồng dạng vì có hệ số khác 0 và có cùng phần biến là x2yzx2yz.
Ta có:
−4yzx2+4x2yz=(−4+4)x2yz=0−4yzx2+4x2yz=(−4+4)x2yz=0
−4yzx2−4x2=(−4−4)x2yz=−8x2yz−4yzx2−4x2=(−4−4)x2yz=−8x2yz
HĐ4 trang 10 Toán 8 Tập 1: Cho hai đa thức A=5x2−4xy+2x−4x2+xyA=5x2−4xy+2x−4x2+xy; B=x2−3xy+2xB=x2−3xy+2x.
Tính giá trị của AA và BB tại x=−2x=−2; y=13y=13. So sánh hai kết quả nhận được.
Lời giải:
Thay x=−2x=−2; y=13y=13 vào đa thức AA ta có:
A=5.(−2)2−4.(−2).13+2.(−2)−4.(−2)2+(−2).13A=5.4−−83+(−4)−4.4+−23A=20+83−4−16+−23A=2
Thay x=−2; y=13 vào đa thức B ta có:
B=(−2)2−3.(−2).13+2.(−2)B=4−(−2)+(−4)B=4+2−4B=2
Vậy A=B
Thực hành 4 trang 10 Toán 8 Tập 1: Thu gọn và tìm bậc của mỗi đa thức sau:
Lời giải:
a) Ta có:
A=x−2y+xy−3x+y2
=(x−3x)−2y+xy+y2
=−2x−2y+xy+y2
Bốn hạng tử của A lần lượt có bậc là 1, 1, 1, 2. Do đó bậc của đa thức A là 2.
b) Ta có:
B=xyz−x2y+xz−12xyz+12xz=(xyz−12xyz)−x2y+(xz+12xz)=12xyz−x2y+32xz
Ba hạng tử của B lần lượt có bậc là 3, 3, 2. Do đó bậc của đa thức B là 3.
Thực hành 5 trang 10 Toán 8 Tập 1: Tính giá trị của đa thức A=3x2y−5xy−2x2y−3xy tại x=3; y=−12.
Lời giải:
Ta có:
A=3x2y−5xy−2x2y−3xy=(3x2y−2x2y)+(−5xy−3xy)=x2y−8xy
Thay x=3; y=−12 vào đa thức A ta có:
A=32.(−12)−8.3.(−12)=−92−(−12)=152
Vậy A=152 khi x=3; y=−12.
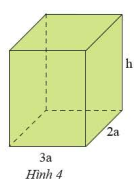
Vận dụng 2 trang 11 Toán 8 Tập 1: Cho hình hộp chữ nhật có các kịch thước như hình 4 (tính theo cm).
a) Viết các biểu thức tính thể tích và diện tích xung quang của hình hộp chữ nhật đó.
b) Tính giá trị của các đại lượng trên khi a=2cm; h=5cm.
Lời giải:
a) Biểu thức tính thể tích của hình hộp chữ nhật: V=3a.2a.h=6a2h
Biểu thức tính diện tích xung quanh của hình hộp chữ nhật: Sxq=(3a+2a).2.h=5a.2.h=10ah
b) Thay a=2cm; h=5cm vào các biểu thức trên ta có:
V=6.22.5=6.4.5=120 (cm3)
Sxq=10.2.5=100 (cm2)
Bài 1 trang 11 Toán 8 Tập 1: Chỉ ra các đơn thức, đa thức trong các biểu thức sau:
−3; 2z; 13xy+1; −10x2yz; 4xy; 5x−z2; 1+1y
Lời giải:
Các đơn thức là: −3; 2z; −10x2yz;
Các đa thức là: 13xy+1; 5x−z2
Bài 2 trang 11 Toán 8 Tập 1: Thu gọn các đơn thức sau. Chỉ ra hệ số, phần biến và bậc của mỗi đơn thức.
Lời giải:
a) Ta có: 5xyx=5.(x.x).y=5x2y.
Đơn thức 5xyx có bậc bằng 2+1=3.
b) Ta có: −xyz23y=−23.x.(y.y).z=−23xy2z
Đơn thức này có bậc bằng 1+2+1=4.
c) Ta có: −2x2(−16)x=(−2).(−16).(x2.x)=13x3
Đơn thức này có bậc bằng 3.
Bài 3 trang 11 Toán 8 Tập 1: Thu gọn và tìm bậc của mỗi đa thức sau:
Lời giải:
a) Ta có:
M=x−3−4y+2x−y
M=(x+2x)+(−4y−y)−3
M=3x−5y−3
Bậc của đa thức M là: 1
b) Ta có:
N=−x2t+13t3+xt2+5t3−4
N=(13t3+5t3)−x2t+xt2−4
N=18t3−x2t+xt2−4
Bài 4 trang 11 Toán 8 Tập 1: Tính giá trị của đa thức P=3xy2−6xy+8xz+xy2−10xz tại x=−3; y=−12; z=3.
Lời giải:
Ta có:
P=3xy2−6xy+8xz+xy2−10xz
P=(3xy2+xy2)+(8xz−10xz)−6xy
P=4xy2−2xz−6xy
Thay x=−3; y=−12; z=3 vào P ta có:
P=4.(−3).(−12)2−2.(−3).3−6.(−3).(−12)
=−3−(−18)−9
=6
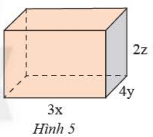
Tính giá trị của V, S khi x=4cm; y=2cm và z=1cm.
Lời giải:
a) Ta có:
V=3x.4y.2z=(3.4.2).xyz=24xyz
S=(3x+4y).2.2z=(3x+4y).4z
b) Thay x=4cm; y=2cm và z=1cm vào các biểu thức V, S ta có:
V=24.4.2.1=192 (cm3)
S=(3.4+4.2).4.1=20.4=80 (cm2).
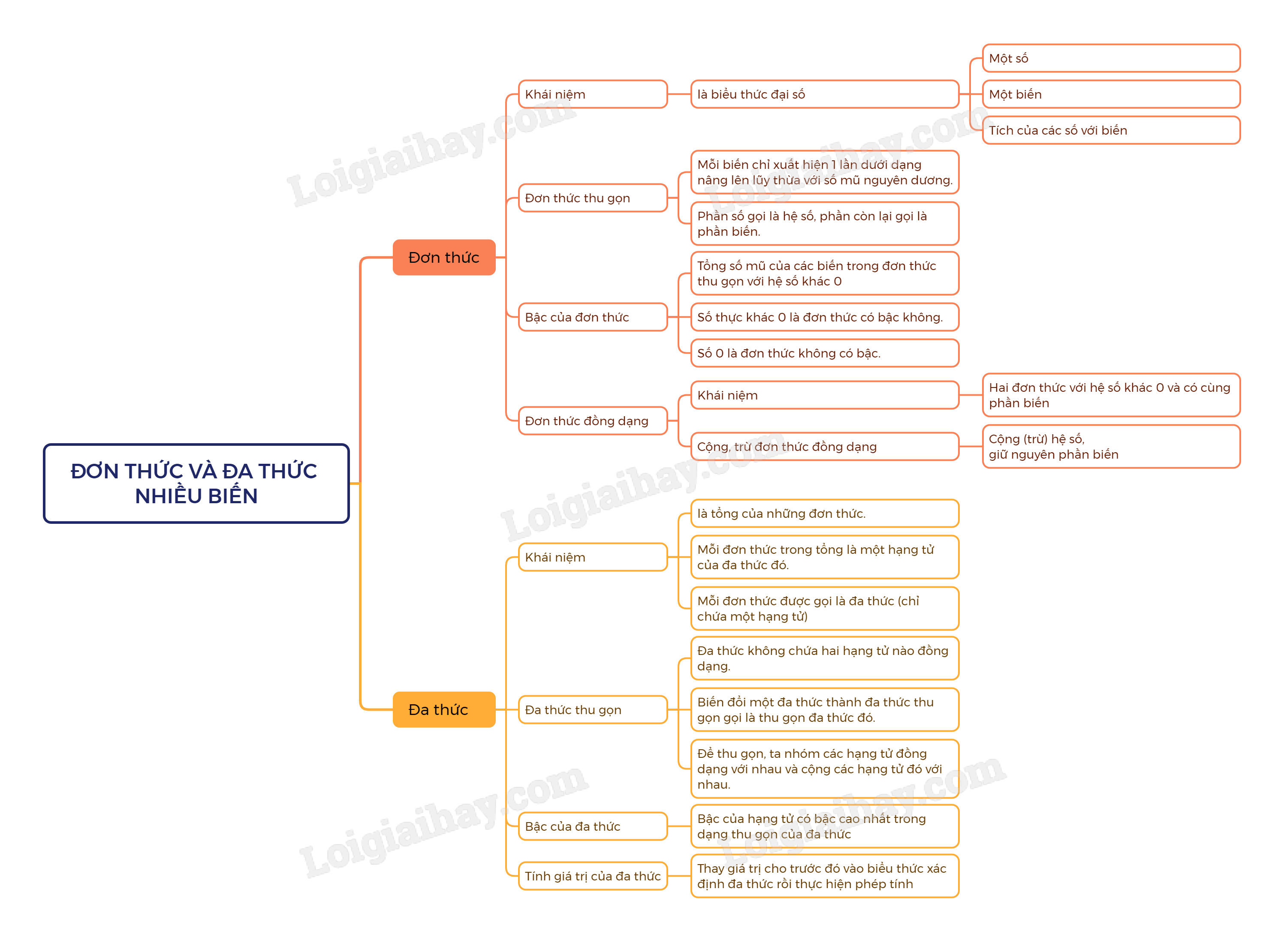
Lý thuyết Đơn thức và đa thức nhiều biến
1. Đơn thức
Đơn thức là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và các biến.
Ví dụ: 1;2xy;−34x2y(−4x);... là các đơn thức.
Đơn thức thu gọn là đơn thức chỉ gồm tích của một số với các biến mà mỗi biến chỉ xuất hiện một lần dưới dạng nâng lên lũy thừa với số mũ nguyên dương.
Ví dụ:
1;2xy;5x2y4z;... là các đơn thức thu gọn.
3x2yx;−34x2y(−4x);... không phải là các đơn thức thu gọn.
Trong một đơn thức thu gọn, phần số còn gọi là hệ số, phần còn lại gọi là phần biến.
Ví dụ: đơn thức 3x3.y có hệ số là 3, phần biến là x3.y.
Tổng số mũ của các biến trong một đơn thức thu gọn với hệ số khác 0 gọi là bậc của đơn thức đó.
Chú ý: + Số thực khác 0 là đơn thức bậc không.
+ Số 0 được gọi là đơn thức không có bậc.
Ví dụ: 2xy có bậc là 1+1=2
5x2y4z có bậc là 2+4+1=7
Hai đơn thức đồng dạng là hai đơn thức có hệ số khác 0 và có cùng phần biến.
Ví dụ:
Hai đơn thức 5x2y4z và −13x2y4z có hệ số khác 0 và có cùng phần biến nên chúng là hai đơn thức đồng dạng.
Hai đơn thức 5x2y4z và 5xy2z không có cùng phần biến nên chúng không phải là hai đơn thức đồng dạng.
Cộng, trừ các đơn thức đồng dạng như thế nào?
Để cộng (hay trừ) các đơn thức đồng dạng, ta cộng (hay trừ) các hệ số với nhau và giữ nguyên phần biến.
Ví dụ:
2x3y2+4x3y2=6x3y24ay2−3ay2=ay2
2. Đa thức
Đa thức là một tổng của những đơn thức.
Mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.
Chú ý: mỗi đơn thức được gọi là một đa thức (chỉ chứa một hạng tử).
Số 0 được gọi là đơn thức không, cũng gọi là đa thức không.
Ví dụ: x2−4x+3;x2+3xyz2−yz+1;(x+3y)+(2x−−y) là đa thức.
x+yx−y,x2+2x2−y2 không phải là đa thức.
x2−4x+3 có 3 hạng tử.
x2+3xyz2−yz+1 có 4 hạng tử.
Đa thức thu gọn là gì?
Đa thức thu gọn là đa thức không chưa hai hạng tử nào đồng dạng.
Thu gọn đa thức như thế nào?
Biến đổi một đa thức thành đa thức thu gọn gọi là thu gọn đa thức đó.
Để thu gọn một đa thức, ta nhóm các hạng tử đồng dạng với nhau và cộng các hạng tử đồng dạng đó với nhau.
Ví dụ:
A=x3−2x2y−x2y+3xy2−y3=x3−3x2y−3xy2−y3
Chú ý: Bậc của hạng tử có bậc cao nhất trong dạng thu gọn của đa thức gọi là bậc của đa thức đó.
Tính giá trị của đa thức như thế nào?
Để tính giá trị của một đa thức tại những giá trị cho trước của các biến, ta thay những giá trị cho trước đó vào biểu thức xác định đa thức rồi thực hiện phép tính.
Ví dụ: Giá trị của biểu thức x2−4xy+3y2 tại x = 2, y = 1 là: 22−4.2.1+3.12=−1
Xem thêm lời giải bài tập Toán 8 Chân trời sáng tạo với cuộc sống hay, chi tiết khác:
Bài 2: Các phép toán với đa thức nhiều biến
Bài 3: Hằng đẳng thức đáng nhớ
Xem thêm các chương trình khác:
- Soạn văn lớp 8 Chân trời sáng tạo (hay nhất)
- Văn mẫu lớp 8 - Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn 8 – Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn lớp 8 – Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn lớp 8 - Chân trời sáng tạo
- Giải SBT Ngữ văn 8 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 8 – Chân trời sáng tạo
- Soạn văn 8 Chân trời sáng tạo (ngắn nhất)
- Giải sgk Tiếng Anh 8 – Friends Plus
- Giải sbt Tiếng Anh 8 - Friends plus
- Trọn bộ Từ vựng Tiếng Anh 8 Friends plus đầy đủ nhất
- Trọn bộ Ngữ pháp Tiếng Anh 8 Friends plus đầy đủ nhất
- Giải sgk Khoa học tự nhiên 8 – Chân trời sáng tạo
- Lý thuyết Khoa học tự nhiên 8 – Chân trời sáng tạo
- Giải sgk Lịch sử 8 – Chân trời sáng tạo
- Lý thuyết Lịch sử 8 - Chân trời sáng tạo
- Giải sbt Lịch sử 8 – Chân trời sáng tạo
- Giải sgk Địa lí 8 – Chân trời sáng tạo
- Lý thuyết Địa lí 8 - Chân trời sáng tạo
- Giải sbt Địa lí 8 – Chân trời sáng tạo
- Giải sgk Giáo dục công dân 8 – Chân trời sáng tạo
- Lý thuyết Giáo dục công dân 8 – Chân trời sáng tạo
- Giải sbt Giáo dục công dân 8 – Chân trời sáng tạo
- Giải sgk Công nghệ 8 – Chân trời sáng tạo
- Lý thuyết Công nghệ 8 - Chân trời sáng tạo
- Giải sbt Công nghệ 8 – Chân trời sáng tạo
- Giải sgk Tin học 8 – Chân trời sáng tạo
- Lý thuyết Tin học 8 - Chân trời sáng tạo
- Giải sbt Tin học 8 – Chân trời sáng tạo
- Giải sgk Hoạt động trải nghiệm 8 – Chân trời sáng tạo