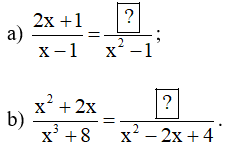Toán 8 Bài 5 (Chân trời sáng tạo): Phân thức đại số

Giải Toán 8 Bài 5: Phân thức đại số

Bài giảng Toán 8 Bài 5: Phân thức đại số - Chân trời sáng tạo

Giải Toán 8 trang 26 Tập 1

Khởi động trang 26 Toán 8 Tập 1: Một ô tô đi được quãng đường s (km) với tốc độ v (km/h) hết thời gian t (giờ).

Hãy lập các biểu thức tính một trong ba đại lượng s, v và t theo hai đại lượng còn lại.

Có phải tất cả các biểu thức đó đều là đa thức? Hãy giải thích.

Lời giải:

Ta lập được các biểu thức tính một trong ba đại lượng s, v và t theo hai đại lượng còn lại như sau: s = vt; v = $\frac{\mathrm{s}}{\mathrm{t}}$; t = $\frac{\mathrm{s}}{\mathrm{v}}$.

Trong ba biểu thức trên, chỉ có biểu thức s = vt là đa thức; hai biểu thức còn lại không phải là đa thức, vì hai biểu thức v = $\frac{\mathrm{s}}{\mathrm{t}}$ và t = $\frac{\mathrm{s}}{\mathrm{v}}$ có chứa phép chia giữa các biến.

1. Phân thức đại số

Khám phá 1 trang 26 Toán 8 Tập 1: a) Viết biểu thức biểu thị các đại lượng sau đây:

• Chiều rộng của hình chữ nhật có chiều dài bằng a (m) và diện tích bằng 3 m².

• Thời gian để một người thợ làm được x sản phẩm, biết rằng mỗi giờ người thợ đó làm được y sản phẩm.

• Năng suất trung bình của một mảnh ruộng gồm hai thửa, một thửa có diện tích a (ha) cho thu hoạch được m tấn lúa, thửa kia có diện tích b (ha) cho thu hoạch n tấn lúa.

b) Các biểu thức trên có đặc điểm nào giống nhau? Chúng có phải là đa thức không?

Lời giải:

a)

• Biểu thức biểu thị chiều rộng của hình chữ nhật có chiều dài bằng a (m) và diện tích bằng 3 m² là: $\frac{3}{\mathrm{a}}$ (m).

• Gọi t là thời gian để người thợ đó làm được x sản phẩm.

Vì thời gian làm việc và số sản phẩm làm được là hai đại lượng tỉ lệ thuận nên ta có:

$\frac{\mathrm{t}}{\mathrm{x}}$ = $\frac{1}{\mathrm{y}}$, suy ra t = $\frac{\mathrm{x}}{\mathrm{y}}$ (giờ)

Vậy biểu thức biểu thị thời gian để người thợ đó làm được x sản phẩm là: $\frac{\mathrm{x}}{\mathrm{y}}$ (giờ).

• Diện tích của mảnh ruộng là: a + b (ha).

Mảnh ruộng cho thu hoạch được số tấn lúa là: m + n (tấn lúa).

Biểu thức biểu thị năng suất trung bình của mảnh ruộng gồm hai thửa đó là: $\frac{\mathrm{a+b}}{\mathrm{m+n}}$ (tấn/ha).

b) Các biểu thức trên đều là biểu thức có dạng $\frac{\mathrm{A}}{\mathrm{B}}$, trong đó A, B là những đa thức và B khác đa thức không.

Do đó các biểu thức này không phải là đa thức.

Giải Toán 8 trang 27 Tập 1

Khám phá 2 trang 27 Toán 8 Tập 1: Cho biểu thức $P=\frac{x^2-1}{2x+1}$

a) Tính giá trị của biểu thức tại x = 0.

b) Tại -$\frac{1}{2}$ , giá trị của biểu thức có xác định không? Tại sao?

Lời giải:

a) Tại x = 0, ta có: $P=\frac{0^2-1}{2.0+1}=\frac{-1}{1}=-1$.

b) Tại ta có mẫu thức có giá trị là: .

Khi đó giá trị của biểu thức P không xác định.

Thực hành 1 trang 27 Toán 8 Tập 1: Tìm giá trị của phân thức:

a) $\frac{x^2-2x+1}{x+2}$ tại x = –3, x = 1;

b) $\frac{xy-3y^2}{x+y}$ tại x = 3, y = –1.

Lời giải:

a) Xét phân thức $\frac{x^2-2x+1}{x+2}$

Điều kiện xác định của phân thức trên là x + 2 ≠ 0, hay x ≠ ‒2.

• Khi x = –3 (điều kiện xác định được thỏa mãn), ta có:

$\frac{{\left(-3\right)}^2-2.\left(-3\right)+1}{\left(-3\right)+2}=\frac{9+6+1}{-1}=-16$

• Khi x = 1 (điều kiện xác định được thỏa mãn), ta có:

$\frac{1^2-2.1+1}{1+2}=\frac{1-2+1}{3}=0$.

b) Xét phân thức $\frac{xy-3y^2}{x+y}$

Điều kiện xác định của phân thức trên là x + y ≠ 0 (nghĩa là các giá trị của x và y thỏa mãn x + y ≠ 0).

Khi x = 3 và y = –1 thì x + y = 2 ≠ 0 nên điều kiện xác định được thỏa mãn.

Khi đó ta có: $\frac{3.\left(-1\right)-3.{\left(-1\right)}^2}{3+\left(-1\right)}=\frac{-3-3}{2}=-3$.

Thực hành 2 trang 27 Toán 8 Tập 1: Viết điều kiện xác định của mỗi phân thức:

a) $\frac{1}{a+4}$ ;

b) $\frac{x{y}^2}{x-2y}$ .

Lời giải:

a) Điều kiện xác định của phân thức $\frac{1}{a+4}$ là a + 4 ≠ 0 hay a ≠ ‒4.

b) Điều kiện xác định của phân thức $\frac{x{y}^2}{x-2y}$ là x – 2y ≠ 0 (nghĩa là tại các giá trị của x và y thỏa mãn x – 2y ≠ 0).

Vận dụng trang 27 Toán 8 Tập 1: Giá thành trung bình của một chiếc áo sơ mi được một xí nghiệp sản xuất cho bởi biểu thức $C\left(x\right)=\frac{0,0002x^2+120x+1000}{x}$ , trong đó x là số áo được sản xuất và C tính bằng nghìn đồng. Tính C khi x = 100, x = 1 000

Lời giải:

• Khi x = 100, thay vào biểu thức C(x) ta được:

$C\left(\mathrm{100}\right)=\frac{0,0002x^2+120x+1000}{x}$

$=\frac{2+12000+1000}{100}=\frac{13002}{100}=130,02$ (nghìn đồng).

• Khi x = 1000, thay vào biểu thức C(x) ta được:

$C\left(\mathrm{1000}\right)=\frac{0,0002x^2+120x+1000}{x}$

$=\frac{200+120000+1000}{1000}=\frac{121200}{1000}=121,2$ (nghìn đồng).

2. Hai phân thức bằng nhau

Giải Toán 8 trang 28 Tập 1

Khám phá 3 trang 28 Toán 8 Tập 1: Xét hai phân thức $M=\frac{x}{y}$ và $N=\frac{x^2-x}{xy-y}$

a) Tính giá trị của các phân thức trên khi x = 3, y = 2 và khi x = ‒1, y = 5.

Nêu nhận xét về giá trị của M và N khi cho x và y nhận những giá trị nào đó (y ≠ 0 và xy – y ≠ 0).

b) Nhân tử thức của phân thức này với mẫu thức của phân thức kia, rồi so sánh hai đa thức nhận được.

Lời giải:

a) • Khi x = 3 và y = 2 ta có: ;

$N=\frac{3^2-3}{3.2-2}=\frac{9-3}{6-2}=\frac{6}{4}=\frac{3}{2}$

• Khi x = ‒1 và y = 5 ta có: ;

$N=\frac{{\left(-1\right)}^2-\left(-1\right)}{\left(-1\right).5-5}=\frac{1+1}{-5-5}=\frac{2}{-10}=\frac{-1}{5}$ .

Nhận xét: Giá trị của M và N bằng nhau khi cho x và y nhận những giá trị thỏa mãn y ≠ 0 và xy – y ≠ 0.

b) • Nhân tử thức của phân thức M với mẫu thức của phân thức N ta được:

x.(xy – y) = x²y – xy.

• Nhân tử thức của phân thức N với mẫu thức của phân thức M ta được:

(x² – x).y = x²y – xy.

Ta thấy cả hai kết quả đều là đa thức x²y – xy nên hai đa thức nhận được bằng nhau.

Thực hành 3 trang 28 Toán 8 Tập 1: Mỗi cặp phân thức sau đây có bằng nhau không? Tại sao?

a) $\frac{x{y}^2}{xy+y}$ và $\frac{xy}{x+1}$;

b) $\frac{xy-x}{y}$ và $\frac{xy-y}{x}$

Lời giải:

a) Ta có: xy².(x + 1) = x²y² + xy²;

(xy + y).xy = x²y² + xy².

Do đó xy².(x + 1) = (xy + y).xy.

Vậy $\frac{x{y}^2}{xy+y}$ = $\frac{xy}{x+1}$.

b) Ta có: (xy – y).y = xy² – y²;

x.(xy – x) = x²y – x².

Do đó (xy – y).y ≠ x.(xy – x)

Vậy hai phân thức $\frac{xy-x}{y}$ và $\frac{xy-y}{x}$ không bằng nhau.

3. Tính chất cơ bản của phân thức

Khám phá 4 trang 28 Toán 8 Tập 1: Xét các phân thức $P=\frac{x^{2}y}{x{y}^2}$, $Q=\frac{x}{y}$, $R=\frac{x^2+xy}{xy+y^2}$

a) Các phân thức trên có bằng nhau không? Tại sao?

b) Có thể biến đổi như thế nào để chuyển Q thành P và R thành Q?

Lời giải:

a) • Xét hai phân thức $P=\frac{x^{2}y}{x{y}^2}$ và $Q=\frac{x}{y}$ ta có:

x²y.y = x²y²;

xy².x = x²y².

Do đó x²y.y = xy².x

Vậy $\frac{x^{2}y}{x{y}^2}$ = $\frac{x}{y}$ hay P = Q (1)

• Xét hai phân thức $Q=\frac{x}{y}$ và $R=\frac{x^2+xy}{xy+y^2}$ ta có:

x.(xy + y²) = x²y + xy²;

y.(x² + xy) = x²y + xy².

Do đó x.(xy + y²) = y.(x² + xy)

Vậy $\frac{x}{y}$ = $\frac{x^2+xy}{xy+y^2}$, hay Q = R (2)

Từ (1) và (2) ta có P = Q = R.

Vậy các phân thức P, Q và Q bằng nhau.

b) • Ta nhân cả tử và mẫu của phân thức $Q=\frac{x}{y}$ với cùng đơn thức xy khác đa thức không thì được: .

• Ta có:$Q=\frac{x}{y}=\frac{x.xy}{y.xy}=\frac{x^{2}y}{x{y}^2}=P$

Ta chia cả tử và mẫu của phân thức R cho cùng nhân tử chung là (x + y) thì được:

$R=\frac{x^2+xy}{xy+y^2}=\frac{x\left(x+y\right)}{y\left(x+y\right)}=\frac{\left[x\left(x+y\right)\right]:\left(x+y\right)}{\left[y\left(x+y\right)\right]:\left(x+y\right)}=\frac{x}{y}$.

Giải Toán 8 trang 29 Tập 1

Thực hành 4 trang 29 Toán 8 Tập 1: Chứng tỏ hai phân thức $\frac{a^2-b^2}{a^{2}b+a{b}^2}$ và $\frac{a-b}{ab}$ bằng nhau theo hai cách khác nhau

Lời giải:

Cách 1:

Xét hai phân thức $\frac{a^2-b^2}{a^{2}b+a{b}^2}$ và $\frac{a-b}{ab}$ ta có:

(a² – b²).ab = a³b – ab³;

(a²b + ab²)(a – b) = a³b – a²b² + a²b² – ab³ = a³b – ab³.

Do đó (a² – b²).ab = (a²b + ab²)(a – b).

Vậy $\frac{a^2-b^2}{a^{2}b+a{b}^2}$ = $\frac{a-b}{ab}$.

Cách 2: Dùng tính chất cơ bản của phân thức

Ta có $\frac{a^2-b^2}{a^{2}b+a{b}^2}=\frac{\left(a+b\right)\left(a-b\right)}{ab\left(a+b\right)}=\frac{a-b}{ab}$.

Vậy $\frac{a^2-b^2}{a^{2}b+a{b}^2}$ = $\frac{a-b}{ab}$.

Giải Toán 8 trang 30 Tập 1

Thực hành 5 trang 30 Toán 8 Tập 1: Rút gọn các phân thức sau:

a) $\frac{3x^2+6xy}{6x^2}$;

b) $\frac{2x^2-x^3}{x^2-4}$;

c) $\frac{x+1}{x^3+1}$.

Lời giải:

a) $\frac{3x^2+6xy}{6x^2}=\frac{3x\left(x+2y\right)}{3x.2x}=\frac{x+2y}{2x}$;

b) $\frac{2x^2-x^3}{x^2-4}=\frac{-x^2\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}=\frac{-x^2}{x+2}$;

c) $\frac{x+1}{x^3+1}=\frac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\frac{1}{x^2-x+1}$.

Bài tập

Bài 1 trang 30 Toán 8 Tập 1: Trong các biểu thức sau, biểu thức nào là phân thức?

$\frac{3x+1}{2x-1}$; 2x² – 5x + 3; $\frac{3x+1}{2x-1}$.

Lời giải:

Trong các biểu thức trên, $\frac{3x+1}{2x-1}$ và 2x² – 5x + 3 là phân thức.

Biểu thức $\frac{3x+1}{2x-1}$ không phải là phân thức, vì $x+\sqrt{x}$ không phải là đa thức.

Bài 2 trang 30 Toán 8 Tập 1: Viết điều kiện xác định của các phân thức sau:

a) $\frac{4x-1}{x-6}$;

b) $\frac{x-10}{x+3y}$;

c) 3x² – x + 7.

Lời giải:

a) Điều kiện xác định của phân thức $\frac{4x-1}{x-6}$ là x – 6 ≠ 0, hay x ≠ 6.

b) Điều kiện xác định của phân thức $\frac{x-10}{x+3y}$ là x + 3y ≠ 0 (nghĩa là tại các giá trị của x và y thỏa mãn x + 3y ≠ 0).

c) Phân thức 3x² – x + 7 xác định với mọi giá trị x ∈ ℝ.

Bài 3 trang 30 Toán 8 Tập 1: Tìm giá trị của phân thức:

a) $A=\frac{3x^2+3x}{x^2+2x+1}$ tại x = ‒ 4;

b) $B=\frac{ab-b^2}{a^2-b^2}$ tại a = 4, b = ‒2.

Lời giải:

a) Xét phân thức $A=\frac{3x^2+3x}{x^2+2x+1}=\frac{3x\left(x+1\right)}{{\left(x+1\right)}^2}$

Điều kiện xác định của phân thức A là (x + 1)² ≠ 0, hay x + 1 ≠ 0, do đó x ≠ –1.

Với điều kiện xác định x ≠ –1 thì $A=\frac{3x^2+3x}{x^2+2x+1}=\frac{3x\left(x+1\right)}{{\left(x+1\right)}^2}=\frac{3x}{x+1}$.

Tại x = ‒ 4 (điều kiện xác định được thỏa mãn), ta có:

$A=\frac{3.\left(-4\right)}{\left(-4\right)+1}=\frac{-12}{-3}=4$.

b) Xét phân thức $B=\frac{ab-b^2}{a^2-b^2}$.

Điều kiện xác định của phân thức B là a² – b² ≠ 0 (nghĩa là các giá trị của a và b thỏa mãn a² – b² ≠ 0).

Với điều kiện xác định trên thì $B=\frac{ab-b^2}{a^2-b^2}=\frac{b\left(a-b\right)}{\left(a+b\right)\left(a-b\right)}=\frac{b}{a+b}$.

Tại a = 4 và b = ‒2 thì a² – b² = 12 ≠ 0 nên điều kiện xác định được thỏa mãn.

Khi đó, $B=\frac{-2}{4+\left(-2\right)}=\frac{-2}{2}=-1$.

Bài 4 trang 30 Toán 8 Tập 1: Mỗi cặp phân thức sau có bằng nhau không? Tại sao?

a) $\frac{3ac}{a^{3}b}$ và $\frac{6c}{2a^{2}b}$;

b) $\frac{3ab-3b^2}{6b^2}$ và $\frac{a-b}{2b}$.

Lời giải:

a) Xét hai phân thức $\frac{3ac}{a^{3}b}$ và $\frac{6c}{2a^{2}b}$ ta có:

3ac.2a²b = 6a³bc;

a³b.6c = 6a³bc.

Do đó 3ac.2a²b = a³b.6c

Vậy $\frac{3ac}{a^{3}b}$ = $\frac{6c}{2a^{2}b}$.

b) Ta có: $\frac{3ab-3b^2}{6b^2}=\frac{3b\left(a-b\right)}{3b.2b}=\frac{a-b}{2b}$.

Vậy $\frac{3ab-3b^2}{6b^2}=\frac{a-b}{2b}$.

Bài 5 trang 30 Toán 8 Tập 1: Tìm đa thức thích hợp thay vào trong các đẳng thức sau:

Lời giải:

a) Ta có $\frac{2x+1}{x-1}=\frac{\left(2x+1\right).\left(x+1\right)}{\left(x-1\right).\left(x+1\right)}=\frac{2x^2+2x+x+1}{x^2-1}=\frac{2x^2+3x+1}{x^2-1}$

Vậy đa thức thay vào là: 2x² + 3x + 1.

b) Ta có $\frac{x^2+2x}{x^3+8}=\frac{x\left(x+2\right)}{\left(x+2\right)\left(x^2-2x+4\right)}=\frac{x}{x^2-2x+4}$.

Vậy đa thức thay vào là: x.

Bài 6 trang 30 Toán 8 Tập 1: Rút gọn các phân thức sau:

b) $\frac{3x^2-3x}{x-1}$;

c) $\frac{a{b}^2-a^{2}b}{2a^2+a}$;

d) $\frac{12\left(x^4-1\right)}{18\left(x^2-1\right)}$.

Lời giải:

a) $\frac{3x^{2}y}{2x{y}^5}=\frac{xy.3x}{xy.2y^4}=\frac{3x}{2y^4}$;

b) $\frac{3x^2-3x}{x-1}=\frac{3x\left(x-1\right)}{x-1}=\frac{3x}{1}=3x$;

c) $\frac{a{b}^2-a^{2}b}{2a^2+a}=\frac{a\left(b^2-ab\right)}{a\left(2a+1\right)}=\frac{b^2-ab}{2a+1}$;

d) $\frac{12\left(x^4-1\right)}{18\left(x^2-1\right)}=\frac{\mathrm{6.2.}\left(x^2+1\right)\left(x^2-1\right)}{\mathrm{6.3.}\left(x^2-1\right)}=\frac{2.\left(x^2+1\right)}{3}=\frac{2x^2+2}{3}$.

Lý thuyết Phân thức đại số

1. Khái niệm phân thức đại số

Một phân thức đại số (hay còn gọi là phân thức) là một biểu thức có dạng $\frac{A}{B}$, trong đó A, B là những đa thức và B khác đa thức 0.

A được gọi là tử thức (hay tử), B được gọi là mẫu thức (hay mẫu).

Chú ý: Mỗi đa thức được coi là một phân thức với mẫu thức bằng 1.

Ví dụ: $\frac{2x+1}{x-3};\frac{ab}{a+b};x^2+3x+2;\sqrt{2}$ là các phân thức đại số.

$\sqrt{x};\sqrt[3]{x}$ không phải là phân thức vì $\sqrt{x};\sqrt[3]{x}$ không phải là đa thức.

2. Điều kiện xác định của phân thức

Điều kiện xác định của phân thức $\frac{A}{B}$ là điều kiện của biến để mẫu thức B khác 0.

Khi thay các biến của phân thức đại số bằng các giá trị nào đó (sao cho phân thức xác định), rồi thực hiện các phép tính thì ta nhận được giá trị của phân thức đại số đó tại các giá trị của biến.

Ví dụ: Phân thức P = $\frac{x+3}{x-1}$ xác định khi $x-1\ne 0$ hay $x\ne 1$

Tại x = 3, $P=\frac{3+3}{3-1}=\frac{6}{2}=3$

3. Hai phân thức bằng nhau

Ta nói hai phân thức $\frac{A}{B}$ và $\frac{C}{D}$ bằng nhau nếu A.D = B.C. Khi đó, ta viết

$\frac{A}{B}=\frac{C}{D}$.

Ví dụ: Hai phân thức $\frac{x{y}^2}{xy+y}$ và $\frac{xy}{x+1}$ bằng nhau.

4. Tính chất

Khi nhân cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức không thì được một phân thức bằng phân thức đã cho.

$\frac{A}{B}=\frac{A.C}{B.C}$ (C là một đa thức khác đa thức không).

Khi chia cả tử và mẫu của một phân thức cho cùng một nhân tử chung của chúng thì được một phân thức bằng phân thức đã cho.

$\frac{A}{B}=\frac{A:D}{B:D}$ (D là một đa thức nhân tử chung).

Ví dụ: Để biến đổi phân thức $\frac{x-y}{y^2-x^2}$ thành $\frac{-1}{x+y}$, ta chia cả tử và mẫu của phân thức $\frac{x-y}{y^2-x^2}$ cho y – x, khi đó $\frac{x-y}{y^2-x^2}=\frac{-(y-x)}{(y-x)(y+x)}=\frac{-1}{x+y}$

Xem thêm lời giải bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 6: Cộng, trừ phân thức

Bài 7: Nhân, chia phân thức

Bài tập cuối chương 1

Bài 1: Hình chóp tam giác đều – Hình chóp tứ giác đều

Bài 2: Diện tích xung quanh và thể tích của hình chóp tam giác đều, hình chóp tứ giác đều