Giải Toán 8 trang 86 Tập 2 Chân trời sáng tạo
Với giải bài tập Toán 8 trang 86 Tập 2 trong Bài tập cuối chương 8 trang 84 sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 8 trang 86 Tập 2.
Giải Toán 8 trang 86 Tập 2
Lời giải:
Ta có
Suy ra .
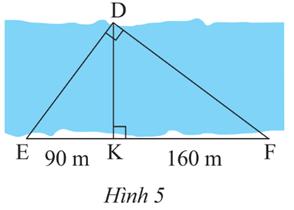
Xét hai tam giác vuông DKE và FKD có:
Suy ra ΔDKE ᔕ ΔFKD (g.g)
Nên hay DK2 = KE.KF
Do đó DK2 = 90.160 =14 400 suy ra DK = 120 m.
Vậy khoảng cách DK bằng 120 m.
Lời giải:
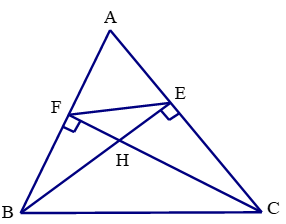
a) Xét tam giác vuông AEB và AFC có:
chung
Suy ra ΔAEB ᔕ ΔAFC (g.g)
b) Xét tam giác vuông HCE và HBF ta có:
(hai góc đối đỉnh)
Suy ra ΔHCE ᔕ ΔHBF (g.g)
Nên hay
c) Xét tam giác HEF và HCB ta có:
(cmt)
(hai góc đối đỉnh)
Suy ra ΔHEF ᔕ ΔHCB (c.g.c).
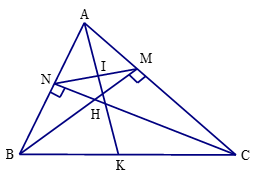
Bài 15 trang 86 Toán 8 Tập 2: Cho tam giác ABC nhọn có hai đường cao BM, CN cắt nhau tại H.
a) Chứng minh rằng ΔAMN ᔕ ΔABC.
b) Phân giác của cắt MN và BC lần lượt tại I và K. Chứng minh rằng .
Lời giải:
a) Xét tam giác vuông ABM và ACN có:
chung
Suy ra ΔABM ᔕ ΔACN (g.g)
Nên hay
Xét tam giác AMN và ABC ta có:
chung
Suy ra ΔAMN ᔕ ΔABC (c.g.c).
b) ΔAMN ᔕ ΔABC, AK là phân giác của
Suy ra
Xét tam giác AIM và AKB ta có:
(vì AK là phân giác )
Suy ra ΔAIM ᔕ ΔAKB nên (1)
Xét tam giác AIN và AKC ta có:
(vì AK là phân giác )
Suy ra ΔAIN ᔕ ΔAKC nên (2)
Từ (1) và (2) suy ra hay .
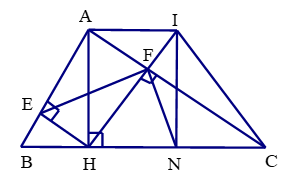
Bài 16 trang 86 Toán 8 Tập 2: Cho tam giác ABC vuông tại A (AB < AC). Kẻ đường cao AH (H ∈ BC).
a) Chứng minh rằng ΔABH ᔕ ΔCBA, suy ra AB2 = BH.BC.
b) Vẽ HE vuông góc với AB tại E, vẽ HF vuông góc với AC tại F. Chứng minh rằng AE.AB = AF.AC.
c) Chứng minh rằng ΔAFE ᔕ ΔABC.
Lời giải:
a) Xét tam giác vuông ABH và CBA ta có:
chung
Suy ra ΔABH ᔕ ΔCBA nên hay AB2 = BH.BC
b) c) Tứ giác AEHF có 4 góc vuông suy ra AEHF là hình chữ nhật
Do đó
ΔABH ᔕ ΔCBA nên
Xét tam giác AEF và ACB ta có:
chung
Suy ra ΔAEF ᔕ ΔACB (g.g) nên hay AE.AB = AF.AC
d) Xét tam giác vuông HNI và HFC ta có:
chung
Suy ra ΔHNI ᔕ ΔHFC (g.g)
Nên hay
Xét tam giác HNF và HIC ta có:
chung
Suy ra ΔHNF ᔕ ΔHIC (c.g.c).
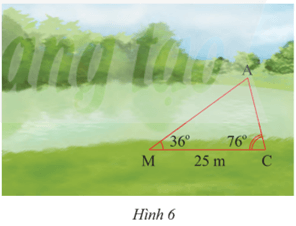
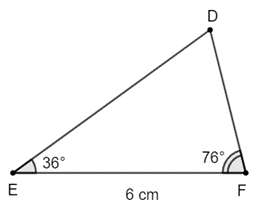
Bài 17 trang 86 Toán 8 Tập 2: Quan sát Hình 6. Vẽ vào tờ giấy tam giác DEF với EF = 4 cm, .
Lời giải:
a) Xét tam giác DEF và AMC có:
Suy ra ΔDEF ᔕ ΔAMC (g.g)
b) Đổi 25 m = 2500 cm.
Dùng thước đo độ dài cạnh DF ta được độ dài DF là 3,9 cm.
Vì ΔDEF ᔕ ΔAMC nên (hai cặp cạnh tương ứng có cùng tỉ lệ)
Thay số,
Vậy khoảng cách giữa hai điểm A và C là 1625 cm hay 16,25 m.
Xem thêm Lời giải bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:
Xem thêm Lời giải bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:
Bài 1 trang 84 Toán 8 Tập 2: Trong các khẳng định sau, khẳng định nào đúng? A. Hai tam giác đồng dạng thì bằng nhau...
Bài 2 trang 84 Toán 8 Tập 2: Nếu ΔABC ᔕ ΔMNP theo tỉ số k = 3 thì ΔMNP ᔕ ΔABC theo tỉ số A. . B. . C. 3. D. 9...
Bài 3 trang 84 Toán 8 Tập 2: Nếu tam giác ABC có MN // AB (với M ∈ AC, N ∈ BC) thì
Bài 4 trang 84 Toán 8 Tập 2: Cho ΔABD ᔕ ΔDEF với tỉ số đồng dạng , biết AB = 9 cm. Khi đó DE bằng A. 6 cm...
Bài 5 trang 84 Toán 8 Tập 2: Nếu tam giác ABC và tam giác EFG có thì
Bài 6 trang 84 Toán 8 Tập 2: Cho ΔXYZ ᔕ ΔEFG, biết XY = 6 cm; EF = 8 cm; EG = 12 cm. Khi đó XZ bằng A. 10 cm...
Bài 7 trang 84 Toán 8 Tập 2: Cho ΔABC ᔕ ΔDEF, biết . khi đó số đo bằng
A. 60°...
Bài 9 trang 85 Toán 8 Tập 2: Trong Hình 1, cho biết , AC = 9 cm, AD = 4 cm.
a) Chứng minh tam giác ΔABD ᔕ ΔACB...
Bài 11 trang 85 Toán 8 Tập 2: a) Tính khoảng cách HM của mặt hồ ở Hình 3a. b) Tính khoảng cách MN của một khúc sông ở Hình 3b...
Bài 15 trang 86 Toán 8 Tập 2: Cho tam giác ABC nhọn có hai đường cao BM, CN cắt nhau tại H. a) Chứng minh rằng ΔAMN ᔕ ΔABC...
Bài 16 trang 86 Toán 8 Tập 2: Cho tam giác ABC vuông tại A (AB < AC). Kẻ đường cao AH (H ∈ BC). a) Chứng minh rằng ΔABH ᔕ ΔCBA, suy ra AB2 = BH.BC...
Bài 17 trang 86 Toán 8 Tập 2: Quan sát Hình 6. Vẽ vào tờ giấy tam giác DEF với EF = 4 cm, . a) Chứng minh ΔDEF ᔕ ΔAMC...
Xem thêm Lời giải bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Mô tả xác suất bằng tỉ số
Bài 2: Xác suất lí thuyết và xác suất thực nghiệm
Bài tập cuối chương 9 trang 95
Hoạt động 4: Vẽ đồ thị hàm số bậc nhất y = ax + b bằng phần mềm
Xem thêm các chương trình khác:
- Soạn văn lớp 8 Chân trời sáng tạo (hay nhất)
- Văn mẫu lớp 8 - Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn 8 – Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn lớp 8 – Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn lớp 8 - Chân trời sáng tạo
- Giải SBT Ngữ văn 8 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 8 – Chân trời sáng tạo
- Soạn văn 8 Chân trời sáng tạo (ngắn nhất)
- Giải sgk Tiếng Anh 8 – Friends Plus
- Giải sbt Tiếng Anh 8 - Friends plus
- Trọn bộ Từ vựng Tiếng Anh 8 Friends plus đầy đủ nhất
- Trọn bộ Ngữ pháp Tiếng Anh 8 Friends plus đầy đủ nhất
- Giải sgk Khoa học tự nhiên 8 – Chân trời sáng tạo
- Lý thuyết Khoa học tự nhiên 8 – Chân trời sáng tạo
- Giải sgk Lịch sử 8 – Chân trời sáng tạo
- Lý thuyết Lịch sử 8 - Chân trời sáng tạo
- Giải sbt Lịch sử 8 – Chân trời sáng tạo
- Giải sgk Địa lí 8 – Chân trời sáng tạo
- Lý thuyết Địa lí 8 - Chân trời sáng tạo
- Giải sbt Địa lí 8 – Chân trời sáng tạo
- Giải sgk Giáo dục công dân 8 – Chân trời sáng tạo
- Lý thuyết Giáo dục công dân 8 – Chân trời sáng tạo
- Giải sbt Giáo dục công dân 8 – Chân trời sáng tạo
- Giải sgk Công nghệ 8 – Chân trời sáng tạo
- Lý thuyết Công nghệ 8 - Chân trời sáng tạo
- Giải sbt Công nghệ 8 – Chân trời sáng tạo
- Giải sgk Tin học 8 – Chân trời sáng tạo
- Lý thuyết Tin học 8 - Chân trời sáng tạo
- Giải sbt Tin học 8 – Chân trời sáng tạo
- Giải sgk Hoạt động trải nghiệm 8 – Chân trời sáng tạo