Nội dung bài viết

    Xem thêm

    Tính diện tích của một tam giác đều có cạnh bằng a

    Với giải bài 25 trang 123 sgk Toán lớp 8 Tập 1 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 8. Mời các bạn đón xem:

    1 3,340 13/11/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 8 Bài 3: Diện tích tam giác

    Video Giải Bài 25 trang 123 Toán 8 Tập 1

    Bài 25 trang 123 Toán 8 Tập 1: Tính diện tích của một tam giác đều có cạnh bằng a.

    *Lời giải:

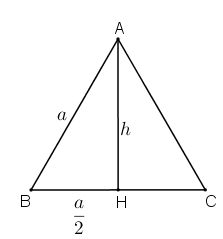
    Tài liệu VietJack

    Xét tam giác đều ABC cạnh a. Dựng đường cao AH.

    Trong tam giác đều, đường cao đồng thời là đường trung tuyến nên H là trung điểm BC.

    BH = CH = a2

    Xét tam giác vuông AHB ta được:

    AH2+HB2=AB2 (định lý Py – ta – go)

    ⇔AH2=AB2−HB2⇔AH2=a2−a22⇔AH2=a2−a24=3a24⇔AH=3a2

    Diện tích tam giác ABC là:

    SABC=12BC.AH

    =12.a.a32=a234(đvdt).

    *Phương pháp giải:

    - Để tính được S tam giác thường:

    + kẻ đường cao từ đỉnh của tam giác đến cạnh đối chính là chiều cao của tam giác

    + Áp dụng công thức tính S tam giác: S = 1/2 . h. cạnh đáy

    *Lý thuyến cần nắm và dạng toán về diện tích tam giác:

    + Tam giác thường:

    Diện tích tam giác bằng nửa tích một cạnh với chiều cao tương ứng.

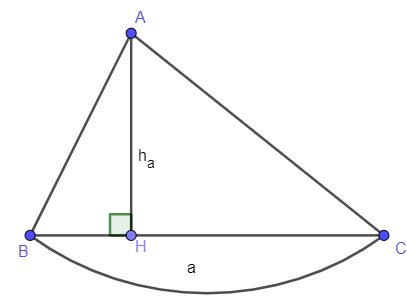
    Tài liệu VietJack

    S = 12a.ha (đơn vị diện tích)

    Với a là độ dài cạnh BC;ha là độ dài đường cao tương ứng với cạnh BC.

    + Tam giác vuông

    Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông

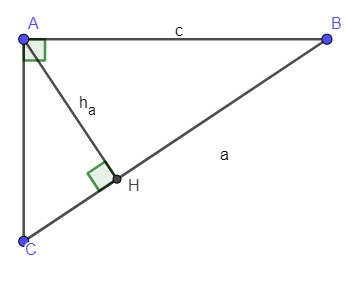
    Tài liệu VietJack

    Cho tam giác ABC vuông tại A có AB = c; AC = b; BC = a; đường cao AH =ha

    Diện tích tam giác vuông ABC: S = 12aha=12bc (đơn vị diện tích).

    Chú ý:

    - Nếu hai tam giác có một cạnh bằng nhau thì tỉ số diện tích hai tam giác đó bằng tỉ số hai đường cao tương ứng với hai cạnh đó.

    - Nếu hai tam giác có một đường cao bằng nhau thì tỉ số diện tích hai tam giác đó bằng tỉ số các cạnh tương ứng.

    Dạng bài tập

    Dạng 1: Tính diện tích tam giác và chứng minh hệ thức về diện tích tam giác

    Phương pháp giải: Sử dụng công thức tính diện tích tam giác

    + Đối với tam giác thường.

    S = 12a.ha (đơn vị diện tích)

    Với a là độ dài cạnh; là độ dài đường cao tương ứng.

    + Đối với tam giác vuông

    S = 12bc (đơn vị diện tích)

    Với b, c là độ dài hai cạnh góc vuông

    Dạng 2: Sử dụng công thức diện tính tích tam giác để tính độ dài các đoạn thẳng, chứng minh hệ thức hình học

    Phương pháp giải:

    + Từ công thức S=12ah ta suy ra công thức h=2Sa và a=2Sh

    a, h là độ dài đáy và chiều cao tương ứng.

    + Phát hiện quan hệ diện tích trong hình rồi sử dụng các công thức trên.

    Dạng 3: Tìm diện tích lớn nhất, nhỏ nhất của một hình

    Phương pháp giải: Để tìm diện tích lớn nhất và nhỏ nhất của một hình ta có thể liên hệ giữa đường vuông góc và đường xiên.

    Chú ý:

    + Nếu diện tích của một hình luôn lớn hơn hoặc bằng một số m và tồn tại vị trí của hình để diện tích bằng m thì m là diện tích nhỏ nhất của hình.

    + Nếu diện tích của một hình luôn nhỏ hơn hoặc bằng một số M và tồn tại vị trí của hình để diện tích bằng M thì M là diện tích lớn nhất của hình.

    Xem thêm các bài viết liên quan hay, chi tiết

    50 bài tập về công thức tính diện tích tam giác (có đáp án 2024) – Toán 8

    50 Bài tập Diện tích tam giác Toán 8 mới nhất

    Xem thêm lời giải bài tập Toán lớp 8 hay, chi tiết khác:

    Câu hỏi trang 121 Toán 8 Tập 1: Hãy cắt một tam giác thành ba mảnh để ghép lại thành...

    Bài 16 trang 121 Toán 8 Tập 1: Giải thích vì sao diện tích của tam giác được tô đậm trong hình 128...

    Bài 17 trang 121 Toán 8 Tập 1: Cho tam giác AOB vuông tại O với đường cao OM...

    Bài 18 trang 121 Toán 8 Tập 1: Cho tam giác ABC và đường trung tuyến AM...

    Bài 19 trang 122 Toán 8 Tập 1: a) Xem hình 133. Hãy chỉ ra các tam giác có cùng diện tích...

    Bài 20 trang 122 Toán 8 Tập 1: Vẽ hình chữ nhật có một cạnh bằng cạnh của một tam giác...

    Bài 21 trang 122 Toán 8 Tập 1: Tính x sao cho diện tích hình chữ nhật. ABCD gấp ba lần...

    Bài 22 trang 122 Toán 8 Tập 1: Tam giác PAF được vẽ trên giấy kẻ ô vuông (h.135)...

    Bài 23 trang 123 Toán 8 Tập 1: Cho tam giác ABC. Hãy chỉ ra một số vị trí của điểm M...

    Bài 24 trang 123 Toán 8 Tập 1: Tính diện tích của một tam giác cân có cạnh đáy bằng a...

    Xem thêm tài liệu khác Toán học lớp 8 hay, chi tiết khác:

    Trắc nghiệm Diện tích tam giác có đáp án

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 3,340 13/11/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: