Nội dung bài viết

    Xem thêm

    Giải Toán 8 trang 65 Tập 2 Cánh diều

    Với giải bài tập Toán 8 trang 65 Tập 2 trong Bài 3: Đường trung bình của tam giác sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 8 trang 65 Tập 2.

    1 177 28/12/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 8 trang 65 Tập 2

    Bài 1 trang 65 Toán 8 Tập 2:Cho tam giác ABC có M là trung điểm của AB, điểm N thuộc cạnh AC thoả mãn MN // BC. Chứng minh NA = NC và MN=12BC.

    Lời giải:

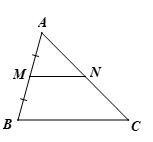
    Bài 1 trang 65 Toán 8 Tập 2 Cánh diều | Giải Toán 8

    Xét ∆ABCvới MN // BC, ta có: AMMB=ANNC (định lí Thalès)

    Mà AM = MB (do M là trung điểm của AB) nên AN = NC.

    Xét ∆ABCvới MN // BC, ta có: AMAB=MNBC (hệ quả của định lí Thalès)

    Mà AM=12AB (do M là trung điềm của AB)

    Suy ra MN=12BC.

    Bài 2 trang 65 Toán 8 Tập 2: Cho tam giác ABC có AM là đường trung tuyến, các điểm N, P phân biệt thuộc cạnh AB sao cho AP = PN = NB. Gọi Q là giao điểm của AM và CP. Chứng minh:

    a) MN // CP;

    b) AQ = QM;

    c) CP = 4PQ.

    Lời giải:

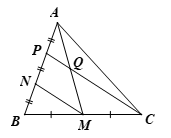
    Bài 2 trang 65 Toán 8 Tập 2 Cánh diều | Giải Toán 8

    a) Do PN = NB nên N là trung điểm của BP.

    Do AM là đường trung tuyến của ∆ABC nên M là trung điểm của BC.

    Xét ∆BCP có M, N lần lượt là trung điểm của BC, BP nên MN là đường trung bình của ∆BCP

    Suy ra MN // CP.

    b) Do AP = PN nên P là trung điểm của AN.

    Mà MN // CP, Q ∈ CP nên MN // PQ.

    Xét ∆AMN có PQ đi qua P là trung điểm của AN và PQ // MN

    Suy ra Q là trung điểm của AM nên AQ = QM.

    c) Xét ∆AMN có P, Q lần lượt là trung điểm của AN, AM nên là đường trung bình của ∆AMN. Do đó PQ=12MN.

    Lại có MN là đường trung bình của ∆BCP nên MN=12CP.

    Khi đó PQ=12MN=12⋅12CP=14CP

    Suy ra CP = 4PQ.

    Bài 3 trang 65 Toán 8 Tập 2: Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.

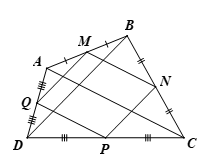
    a) Chứng minh tứ giác MNPQ là hình bình hành.

    b) Cho AC = BD. Chứng minh tứ giác MNPQ là hình thoi.

    c) Cho AC ⊥ BD. Chứng minh tứ giác MNPQ là hình chữ nhật.

    Lời giải:

    Bài 3 trang 65 Toán 8 Tập 2 Cánh diều | Giải Toán 8

    a) Xét ∆ABC có M, N lần lượt là trung điểm AB, BC nên MN là đường trung bình của ∆ABC

    Suy ra MN//AC và MN=12AC (1)

    Xét ∆ADC có P, Q lần lượt là trung điểm DC, AD nên PQ là đường trung bình của ∆ADC

    Suy ra PQ//AC và PQ=12AC (2)

    Từ (1) và (2) suy ra MN // PQ; MN = PQ.

    Tứ giác MNPQ có MN // PQ; MN = PQ nên MNPQ là hình bình hành.

    b) Xét tam giác ABD có M, Q lần lượt là trung điểm AB, AD nên MQ là đường trung bình của ∆ABD

    Suy raMQ // BD và MQ=12BD

    Mà MN=12AC và AC = BD nên MN = MQ.

    Hình bình hành MNPQ có MN = MQ nên MNPQ là hình thoi.

    c) Ta có MN // AC (câu a), MQ // BD (câu b) và AC ⊥ BD (giả thiết)

    Suy ra MN ⊥ MQ hay NMQ^=90°

    Hình bình hành MNPQ có NMQ^=90° nên là hình chữ nhật.

    Bài 4 trang 65 Toán 8 Tập 2: Cho tam giác ABC nhọn có H là trực tâm. Gọi M, N, P, Q lần lượt là trung điểm của các đoạn thẳng AB, BH, HC, CA. Chứng minh tứ giác MNPQ là hình chữ nhật.

    Lời giải:

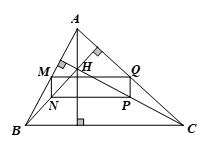
    Bài 4 trang 65 Toán 8 Tập 2 Cánh diều | Giải Toán 8

    ⦁Xét ∆ABH có M, N lần lượt là trung điểm của AB, BH nên MN là đường trung bình ∆ABH.

    Suy ra MN//AH (1)

    Tương tự, xét ∆AHC ta cũng có PQ là đường trung bình ∆AHC nên PQ//AH (2)

    Từ (1) và (2) ta có MN // PQ // AH.

    ⦁ Chứng minh tương tự như trên với ∆ABC và ∆HBC, ta cũng có MQ, NP lần lượt là đường trung bình của ∆ABC và ∆HBC.

    Do đó MQ // BC và NP // BC. Suy ra MQ // NP // BC.

    Tứ giác MNPQ có MN // PQ và MQ // NP nên MNPQ là hình bình hành.

    ⦁ Ta có MN//AH và AH ⊥ BC (do H là trực tâm của ∆ABC) nên MN ⊥ BC

    Lại có NP // BC nên suy ra MN ⊥ NP hay MNP^=90°.

    Hình bình hành MNPQ có MNP^=90°. nên MNPQ là hình chữ nhật.

    Bài 5 trang 65 Toán 8 Tập 2: Trong Hình 36, ba cạnh màu vàng AB, BC, CA gợi nên hình ảnh tam giác ABC và đoạn thẳng màu xanh MN là một đường trung bình của tam giác đó. Bạn Duyên đứng ở phía dưới đo khoảng cách giữa hai chân cột số Bài 5 trang 65 Toán 8 Tập 2 Cánh diều | Giải Toán 8 và số , Bài 5 trang 65 Toán 8 Tập 2 Cánh diều | Giải Toán 8 từ đó ước lượng được độ dài đoạn thẳng MN khoảng 4,5 m. Khoảng cách giữa hai mép dưới của mái được tính bằng độ dài đoạn thẳng BC. Hỏi khoảng cách đó khoảng bao nhiêu mét?

    Bài 5 trang 65 Toán 8 Tập 2 Cánh diều | Giải Toán 8

    Lời giải:

    Xét ∆ABC có MN là đường trung bình của ∆ABC nên MN=12BC

    Suy ra BC = 2MN = 2.4,5 = 9(m).

    Vậy khoảng cách giữa hai mép dưới của mái khoảng 9 m.

    Xem thêm Lời giải bài tập Toán 8 Cánh diều hay, chi tiết khác:

    Giải Toán 8 trang 62 Tập 2

    Giải Toán 8 trang 63 Tập 2

    Giải Toán 8 trang 64 Tập 2

    Giải Toán 8 trang 65 Tập 2

    Xem thêm Lời giải bài tập Toán 8 Cánh diều hay, chi tiết khác: 

    Khởi động trang 62 Toán 8 Tập 2: Hình 28 gợi nên hình ảnh tam giác ABC và đoạn thẳng MN với M, N lần lượt là trung điểm của hai cạnh AB, AC...

    Hoạt động 1 trang 62 Toán 8 Tập 2: Quan sát tam giác ABC ở Hình 29 và cho biết hai đầu mút D, E của đoạn thẳng DE có đặc điểm gì...

    Luyện tập 1 trang 62 Toán 8 Tập 2: Vẽ tam giác ABC và các đường trung bình của tam giác đó...

    Hoạt động 2 trang 63 Toán 8 Tập 2: Cho tam giác ABC có MN là đường trung bình (Hình 31)...

    Luyện tập 2 trang 64 Toán 8 Tập 2: Cho hình thang ABCD (AB // CD). Giả sử M, N, P lần lượt là trung điểm của các đoạn thẳng AD, BC, AC. Chứng minh...

    Bài 1 trang 65 Toán 8 Tập 2:Cho tam giác ABC có M là trung điểm của AB, điểm N thuộc cạnh AC thoả mãn MN // BC. Chứng minh NA = NC và MN=12BC...

    Bài 2 trang 65 Toán 8 Tập 2: Cho tam giác ABC có AM là đường trung tuyến, các điểm N, P phân biệt thuộc cạnh AB sao cho AP = PN = NB. Gọi Q là giao điểm của AM và CP...

    Bài 3 trang 65 Toán 8 Tập 2: Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA...

    Bài 4 trang 65 Toán 8 Tập 2: Cho tam giác ABC nhọn có H là trực tâm. Gọi M, N, P, Q lần lượt là trung điểm của các đoạn thẳng AB, BH, HC, CA...

    Bài 5 trang 65 Toán 8 Tập 2: Trong Hình 36, ba cạnh màu vàng AB, BC, CA gợi nên hình ảnh tam giác ABC và đoạn thẳng màu xanh MN là một đường trung bình của tam giác đó...

    Xem thêm Lời giải bài tập Toán 8 Cánh diều hay, chi tiết khác: 

    Bài 2: Ứng dụng của định lí Thalès trong tam giác

    Bài 4: Tính chất đường phân giác của tam giác

    Bài 5: Tam giác đồng dạng

    Bài 6: Trường hợp đồng dạng thứ nhất của tam giác

    Bài 7: Trường hợp đồng dạng thứ hai của tam giác

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 177 28/12/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: