Giải Toán 11 trang 23 Tập 2 Cánh diều
Với giải bài tập Toán 11 trang 23 Tập 2 trong Bài 2: Ứng dụng của phương trình bậc nhất một ẩn sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 11 trang 23 Tập 2.
Giải Toán 11 trang 23 Tập 2
Lời giải:
⦁ Mỗi cách chọn ra đồng thời 5 viên bi trong hộp có 5 + 6 + 7 = 18 viên bi cho ta một tập hợp chập 5 của 18 phần tử. Do đó, không gian mẫu Ω gồm các tổ hợp chập 5 của 18 phần tử và = 8 458.
⦁ Xét biến cố A: “Chọn được 5 viên bi có đủ ba màu và số bi màu đỏ bằng số bi màu vàng”.
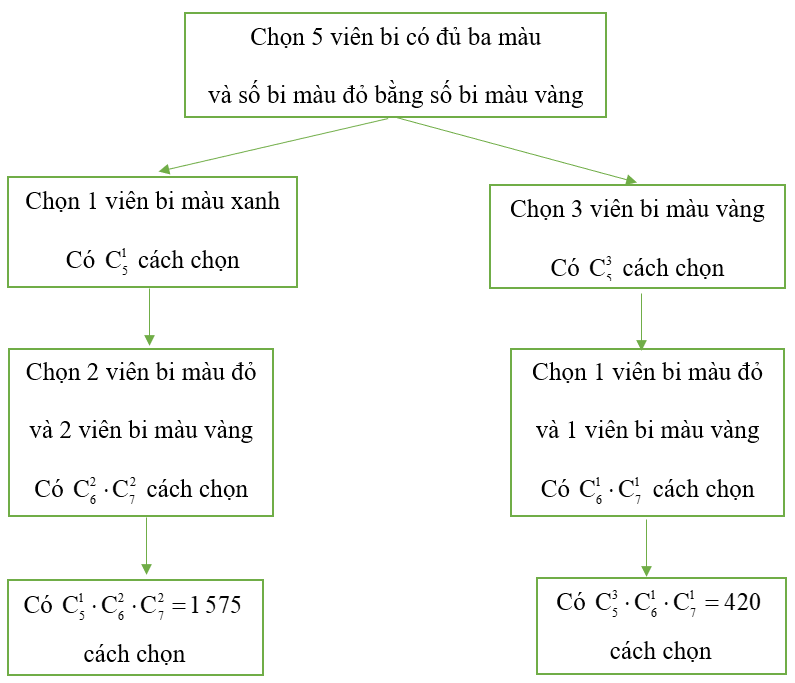
Sơ đồ hình cây biểu thị các khả năng thuận lợi cho biến cố A:
Như vậy, số kết quả thuận lợi cho biến cố A là: n(A) = 1 575 + 420 = 1 995.
Vậy xác suất của biến cố A là: P(A) = .
Xem thêm Lời giải bài tập Toán 11 Cánh diều hay, chi tiết khác:
Xem thêm Lời giải bài tập Toán 11 Cánh diều hay, chi tiết khác:
Hoạt động 6 trang 20 Toán 11 Tập 2: Xét các biến cố độc lập A và B trong Ví dụ 4. a) Tính P(A), P(B) và P(A ∩ B)...
Bài 1 trang 24 Toán 11 Tập 2: Tung một đồng xu cân đối và đồng chất hai lần liên tiếp. Xét các biến cố: A: “Lần thứ nhất xuất hiện mặt ngửa”;...
Bài 2 trang 24 Toán 11 Tập 2: Gieo ngẫu nhiên một xúc xắc cân đối và đồng chất hai lần liên tiếp. Xét các biến cố: A: “Số chấm xuất hiện ở lần gieo thứ nhất lớn hơn 4”;...
Xem thêm Lời giải bài tập Toán 11 Cánh diều hay, chi tiết khác:
Bài 1: Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm
Bài tập cuối chương 5 trang 25
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Cánh diều (hay nhất)
- Văn mẫu lớp 11 - Cánh diều
- Tóm tắt tác phẩm Ngữ văn 11 – Cánh diều
- Tác giả tác phẩm Ngữ văn 11 - Cánh diều
- Giải SBT Ngữ văn 11 – Cánh diều
- Bố cục tác phẩm Ngữ văn 11 – Cánh diều
- Giải Chuyên đề học tập Ngữ văn 11 – Cánh diều
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Cánh diều
- Soạn văn 11 Cánh diều (ngắn nhất)
- Giải sgk Tiếng Anh 11 – ilearn Smart World
- Giải sbt Tiếng Anh 11 - ilearn Smart World
- Trọn bộ Từ vựng Tiếng Anh 11 ilearn Smart World đầy đủ nhất
- Giải sgk Vật lí 11 – Cánh diều
- Lý thuyết Vật lí 11 – Cánh diều
- Giải sbt Vật lí 11 – Cánh diều
- Giải Chuyên đề học tập Vật lí 11 – Cánh diều
- Giải sgk Hóa học 11 – Cánh diều
- Giải Chuyên đề học tập Hóa học 11 – Cánh diều
- Lý thuyết Hóa 11 - Cánh diều
- Giải sbt Hóa học 11 – Cánh diều
- Giải sgk Sinh học 11 – Cánh diều
- Lý thuyết Sinh học 11 – Cánh diều
- Giải Chuyên đề học tập Sinh học 11 – Cánh diều
- Giải sbt Sinh học 11 – Cánh diều
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Cánh diều
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Cánh diều
- Lý thuyết Kinh tế pháp luật 11 – Cánh diều
- Giải sbt Kinh tế pháp luật 11 – Cánh diều
- Giải sgk Lịch sử 11 – Cánh diều
- Giải Chuyên đề học tập Lịch sử 11 – Cánh diều
- Lý thuyết Lịch sử 11 - Cánh diều
- Giải sbt Lịch sử 11 – Cánh diều
- Giải sgk Địa lí 11 – Cánh diều
- Giải Chuyên đề học tập Địa lí 11 – Cánh diều
- Lý thuyết Địa lí 11 - Cánh diều
- Giải sbt Địa lí 11 – Cánh diều
- Giải sgk Công nghệ 11 – Cánh diều
- Lý thuyết Công nghệ 11 - Cánh diều
- Giải sbt Công nghệ 11 – Cánh diều
- Giải sgk Tin học 11 – Cánh diều
- Giải Chuyên đề học tập Tin học 11 – Cánh diều
- Lý thuyết Tin học 11 - Cánh diều
- Giải sbt Tin học 11 – Cánh diều
- Giải sgk Giáo dục quốc phòng an ninh 11 – Cánh diều
- Lý thuyết Giáo dục quốc phòng 11 – Cánh diều
- Giải sbt Giáo dục quốc phòng 11 – Cánh diều
- Giải sgk Hoạt động trải nghiệm 11 – Cánh diều