Giải Toán 10 trang 25 Tập 1 Chân trời sáng tạo
Với giải bài tập Toán lớp 10 trang 25 Tập 1 trong Bài 3: Các phép toán trên tập hợp sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 trang 25 Tập 1.
Giải Toán 10 trang 25 Tập 1
Thực hành 4 trang 25 Toán lớp 10 Tập 1: Xác định các tập hợp sau đây:
Lời giải:
a) Ta có sơ đồ sau:

Vậy (1; 3) [- 2; 2] = [- 2; 3)
b) Ta có sơ đồ sau:

Vậy (- ∞; 1) [0; π] = [0; 1).
c) Ta có sơ đồ sau:
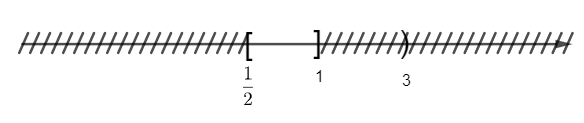
Vậy
d) Ta có sơ đồ sau:

Vậy Cℝ[- 1; + ∞) = (- ∞; -1).
Bài tập
Bài 1 trang 25 Toán lớp 10 Tập 1: Xác định các tập hợp A ∪ B và A ∩ B với:
a) A = {đỏ; cam; vàng; lục; lam}, B = {lục; lam; chàm; tím};
b) A là tập hợp các tam giác đều, B là tập hợp các tam giác cân.
Lời giải:
a) Ta có tập là tập các phần tử thuộc tập A hoặc thuộc tập B nên = {đỏ; cam; vàng; lục; lam; tràm; tím}.
Tập hợp là tập các phần tử vừa thuộc tập A vừa thuộc B nên = {lục; lam}.
Vậy = {đỏ; cam; vàng; lục; lam; tràm; tím} và = {lục; lam}.
b) Mọi tam giác đều đều là tam giác cân nên tập A B. Do đó = B và .
Vậy = B và .
Bài 2 trang 25 Toán lớp 10 Tập 1: Xác định tập hợp A ∩ B trong mỗi trường hợp sau:
a) A = {x ∈ ℝ | x2 – 2 = 0}, B = {x ∈ ℝ | 2x – 1 < 0};
b) A = {(x; y)| x, y ∈ ℝ , y = 2x – 1}, B = {(x; y)| x, y ∈ ℝ, y = - x + 5};
c) A là tập hợp các hình thoi, B là tập hợp các hình chữ nhật.
Lời giải:
a) Ta có x2 – 2 = 0 ⇔ x2 = 2 ⇔ ⇒ A = { }.
Ta lại có 2x – 1 < 0 ⇔ x < . Khi đó B = ()
Tập A∩B gồm các phần tử vừa thuộc tập hợp A vừa thuộc tập hợp B nên =
b) Vì (x; y) nên (x; y) thỏa mãn hệ sau:
Vậy = {(2; 3)}
c) Ta thấy hình vuông vừa là hình chữ nhật và cũng là hình thoi. Do đó là tập hợp các hình vuông.
Vậy tập là tập hợp các hình vuông.
Lời giải:
Tập hợp E gồm các số tự nhiên nhỏ hơn 10 nên E = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}.
Tập hợp A gồm các phần tử thuộc tập E và thỏa mãn là bội của 3 nên A = {0; 3; 6; 9}.
Tập hợp B gồm các phần tử thuộc tập E và thỏa mãn là ước của 6 nên B = {1; 2; 3; 6}.
Khi đó:
Tập hợp A\B là tập các phần tử thuộc tập A nhưng không thuộc tập B nên A \ B = {0; 9}.
Tập hợp B\A là tập các phần tử thuộc tập B nhưng không thuộc tập A nên B\A = {1; 2}.
Vì A là tập con của tập E nên tập hợp CEA là tập phần bù của tập hợp A trong tập E được xác định là CEA = {1; 2; 4; 5; 7; 8}.
Vì B là tập con của tập E nên tập hợp CEB là tập phần bù của tập hợp B trong tập E được xác định là CEB = {0; 4; 5; 7; 8; 9}
Tập hợp A∪B là tập các phần tử thuộc tập hợp A hoặc tập hợp B nên = {0; 1; 2; 3; 6; 9}.
Do A∪B là tập con của tập hợp E nên tập phần bù của tập A∪B trong E được xác định là = {4; 5; 7; 8}.
Tập hợp A∩B là tập các phần tử vừa thuộc tập hợp A vừa thuộc tập hợp B nên = {3; 6}.
Do A∩B là tập con của tập E nên tập phần bù của tập A∩B trong tập E được xác định là = {0; 1; 2; 4; 5; 7; 8; 9}.
Lời giải:
a) Tập hợp A là con của tập hợp vì tập hợp gồm các phần tử hoặc thuộc A hoặc thuộc B nên các phần tử của tập hợp A đều thuộc tập hợp .
Biểu đồ ven:
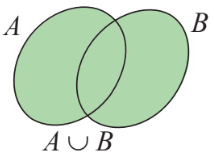
b) Tâp hợp là tập con của tập hợp A vì, tập hợp gồm các phần tử vừa thuộc A vừa thuộc B nên các phần tử của tập đều thuộc tập hợp A.
Biểu đồ ven:
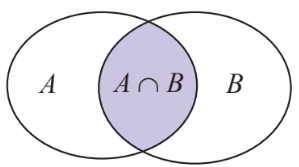
a) có bao nhiêu học sinh thích ít nhất một trong hai môn Toán và Tiếng Anh?
b) có bao nhiêu học sinh không thích cả hai môn này?
Lời giải:
a) Ta có biểu đồ ven như sau:
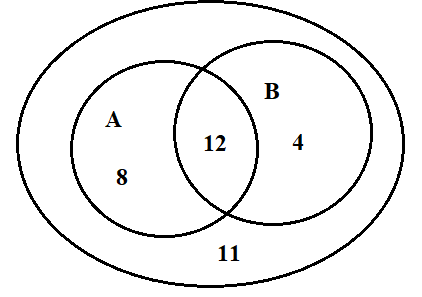
Gọi tập hợp A là tập các học sinh thích học môn Toán, tập hợp B là tập các học sinh thích môn Tiếng Anh. Khi đó n(A) = 20 và n(B) = 16 và n(A∩B) = 12.
Số học sinh thích ít nhất một trong hai môn Toán hoặc Tiếng Anh là:
n(A∪B) = n(A) + n(B) - n(A∩B) = 20 + 16 – 12 = 24.
Vậy có 24 học sinh thích ít nhất một trong hai môn Toán hoặc Tiếng Anh.
b) Số học sinh không thích cả hai môn này là 35 – 24 = 11.
Vậy có 11 học sinh không thích cả hai môn Toán và Tiếng Anh.
Bài 6 trang 25 Toán lớp 10 Tập 1: Xác định các tập hợp sau đây:
Lời giải:
a) Ta có sơ đồ sau:
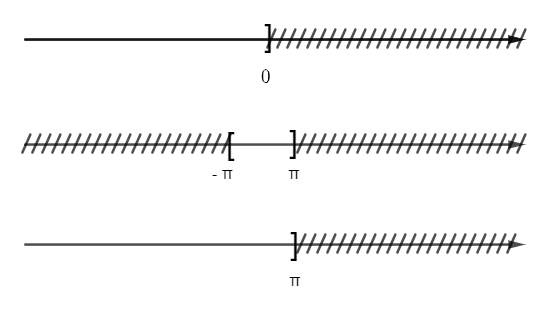
Vậy = (- ∞; π]
b) Ta có sơ đồ sau:
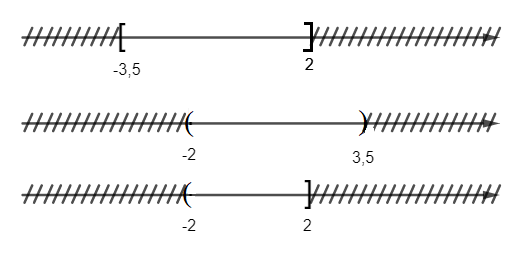
Vậy [– 3,5; 2] ∩ ( – 2; 3,5) = (- 2; 2].
c) Ta có sơ đồ sau:
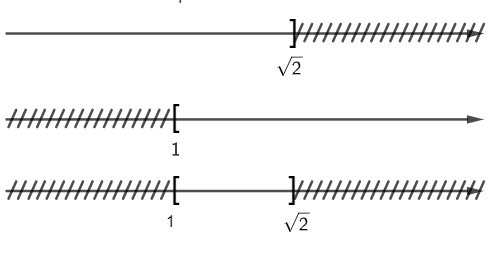
Vậy
d) Ta có sơ đồ sau:
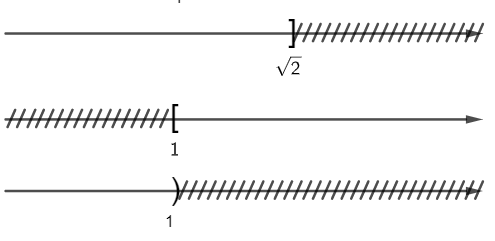
Vậy = (- ∞; 1).
Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Bất phương trình bậc nhất hai ẩn
Xem thêm các chương trình khác:
- Soạn văn lớp 10 (hay nhất) – Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn lớp 10 – Chân trời sáng tạo
- Soạn văn lớp 10 (ngắn nhất) – Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn lớp 10 – Chân trời sáng tạo
- Giải sbt Ngữ văn lớp 10 – Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn lớp 10 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 10 – Chân trời sáng tạo
- Văn mẫu lớp 10 – Chân trời sáng tạo
- Giải Chuyên đề học tập Ngữ văn 10 – Chân trời sáng tạo
- Giải sgk Tiếng Anh 10 Friends Global – Chân trời sáng tạo
- Giải sbt Tiếng Anh 10 Friends Global – Chân trời sáng tạo
- Trọn bộ Từ vựng Tiếng Anh 10 Friends Global đầy đủ nhất
- Ngữ pháp Tiếng Anh 10 Friends Global
- Giải sgk Vật lí 10 – Chân trời sáng tạo
- Giải sbt Vật lí 10 – Chân trời sáng tạo
- Lý thuyết Vật lí 10 – Chân trời sáng tạo
- Giải Chuyên đề Vật lí 10 – Chân trời sáng tạo
- Giải sgk Hóa học 10 – Chân trời sáng tạo
- Lý thuyết Hóa học 10 – Chân trời sáng tạo
- Giải sbt Hóa học 10 – Chân trời sáng tạo
- Giải Chuyên đề Hóa học 10 – Chân trời sáng tạo
- Giải sgk Sinh học 10 – Chân trời sáng tạo
- Giải sbt Sinh học 10 – Chân trời sáng tạo
- Lý thuyết Sinh học 10 – Chân trời sáng tạo
- Giải Chuyên đề Sinh học 10 – Chân trời sáng tạo
- Giải sgk Lịch sử 10 – Chân trời sáng tạo
- Giải sbt Lịch sử 10 – Chân trời sáng tạo
- Giải Chuyên đề Lịch sử 10 – Chân trời sáng tạo
- Lý thuyết Lịch sử 10 – Chân trời sáng tạo
- Giải sgk Địa lí 10 – Chân trời sáng tạo
- Lý thuyết Địa Lí 10 - Chân trời sáng tạo
- Giải sbt Địa lí 10 – Chân trời sáng tạo
- Giải Chuyên đề Địa lí 10 – Chân trời sáng tạo
- Giải sgk Giáo dục Kinh tế và Pháp luật 10 – Chân trời sáng tạo
- Giải sbt Giáo dục Kinh tế và Pháp luật 10 – Chân trời sáng tạo
- Giải Chuyên đề Kinh tế và pháp luật 10 – Chân trời sáng tạo
- Lý thuyết KTPL 10 – Chân trời sáng tạo
- Giải sgk Hoạt động trải nghiệm 10 – Chân trời sáng tạo
- Giải sbt Hoạt động trải nghiệm 10 – Chân trời sáng tạo
- Giải sgk Giáo dục thể chất 10 – Chân trời sáng tạo
