Giải Toán 10 Bài 3 (Cánh diều): Phương trình đường thẳng

Giải bài tập Toán 10 Bài 3: Phương trình đường thẳng

A. Các câu hỏi trong bài

Giải Toán 10 trang 73 Tập 2

Câu hỏi khởi động trang 73 Toán 10 Tập 2: Một máy bay cất cánh từ sân bay theo một đường thẳng nghiêng với phương nằm ngang một góc 20°, vận tốc cất cánh là 200 km/h. Hình 24 minh họa hình ảnh đường bay của máy bay trên ra màn hình ra đa của bộ phận không lưu. Để xác định vị trí của máy bay tại những thời điểm quan trọng (chẳng hạn: 30 s, 60 s, 90 s, 120 s), người ta phải lập phương trình đường thẳng mô tả đường bay.

Làm thế nào để lập phương trình đường thẳng trong mặt phẳng tọa độ?

Lời giải

Sau bài học ta sẽ biết cách để lập phương trình đường thẳng trong mặt phẳng tọa độ, ta cần biết 1 điểm đi qua và 1 vectơ chỉ phương hoặc vectơ pháp tuyến của đường thẳng đó.

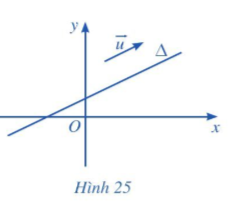
Hoạt động 1 trang 73 Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆. Vẽ vectơ $\overrightarrow{u}\left(\overrightarrow{u}\ne \overrightarrow{0}\right)$ có giá song song (hoặc trùng) với đường thẳng ∆ (Hình 25).

Lời giải

Giá của vectơ là đường thẳng đi qua 2 đầu mút của vectơ. Vậy ta vẽ như sau:

+ Vẽ một đoạn thẳng bất kì song song hoặc trùng với đường thẳng ∆.

+ Đánh dấu mũi tên chiều trên đoạn thẳng đó, ta được một vectơ thỏa mãn yêu cầu bài toán.

Giải Toán 10 trang 74 Tập 2

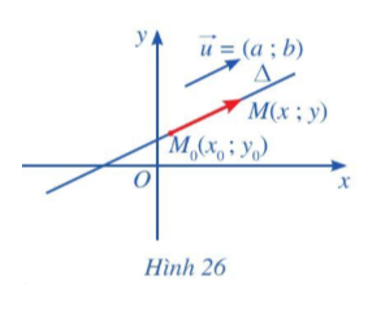
Hoạt động 2 trang 74 Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆ đi qua điểm M₀(x₀; y₀) và có vectơ chỉ phương $\overrightarrow{u}=\left(a;b\right)$. Xét điểm M(x; y) nằm trên ∆ (Hình 26).

a) Nhận xét về phương của hai vectơ $\overrightarrow{u}$ và $\overrightarrow{M_{0}M}$.

b) Chứng minh có số thực t sao cho $\overrightarrow{M_{0}M}=t\overrightarrow{u}$.

c) Biểu diễn tọa độ của điểm M qua tọa độ của điểm M₀ và tọa độ của vectơ chỉ phương $\overrightarrow{u}$.

Lời giải

a) Đường thẳng ∆ đi qua hai điểm M₀ và M hay đường thẳng ∆ chính là đường thẳng MM₀. Khi đó giá của vectơ $\overrightarrow{M_{0}M}$ là đường thẳng ∆. (1)

Vectơ $\overrightarrow{u}$ là vectơ chỉ phương của đường thẳng ∆ nên giá của vectơ $\overrightarrow{u}$song song hoặc trùng với đường thẳng ∆. (2)

Từ (1) và (2) suy ra hai vectơ $\overrightarrow{u}$ và $\overrightarrow{M_{0}M}$ có giá song song hoặc trùng nhau.

Vậy hai vectơ $\overrightarrow{u}$ và $\overrightarrow{M_{0}M}$ cùng phương.

b) Hai vectơ $\overrightarrow{u}$ và $\overrightarrow{M_{0}M}$ cùng phương nên có số thực t sao cho $\overrightarrow{M_{0}M}=t\overrightarrow{u}$.

c) Ta có: $\overrightarrow{M_{0}M}=\left(x-x_0;y-y_0\right),\overrightarrow{u}=\left(a;b\right)$.

Vậy $\overrightarrow{M_{0}M}=t\overrightarrow{u}$ $\iff \left\{\begin{array}{l}x-x_0=ta\\ y-y_0=tb\end{array}\right.\iff \left\{\begin{array}{l}x=x_0+at\\ y=y_0+bt\end{array}\right.$.

Giải Toán 10 trang 75 Tập 2

Luyện tập 1 trang 75 Toán 10 Tập 2: Cho đường thẳng Δ có phương trình tham số

$\left\{\begin{array}{l}x=1-2t\\ y=-2+t.\end{array}\right.$

a) Chỉ ra tọa độ của hai điểm thuộc đường thẳng Δ.

b) Điểm nào trong các điểm C(– 1; – 1), D(1; 3) thuộc đường thẳng Δ.

Lời giải

a) Đường thẳng ∆ có phương trình tham số là $\left\{\begin{array}{l}x=1-2t\\ y=-2+t\end{array}\right.$.

- Thay t = 1 vào phương trình tham số của ∆ ta có: $\left\{\begin{array}{l}x=1-2.1=-1\\ y=-2+1=-1\end{array}\right.$.

Vậy điểm A(–1; – 1) thuộc đường thẳng ∆.

- Thay t = 2 vào phương trình tham số của ∆ ta có $\left\{\begin{array}{l}x=1-2.2=-3\\ y=-2+2=0\end{array}\right.$.

Điểm B(– 3; 0) thuộc đường thẳng ∆.

b) - Từ câu a) ta thấy điểm A(– 1; – 1) thuộc đường thẳng Δ ứng với t = 1.

Mà C ≡ A.

Vậy điểm C(– 1; – 1) thuộc đường thẳng ∆.

- Thay tọa độ điểm D(1; 3) vào phương trình tham số của đường thẳng Δ ta được:

$\left\{\begin{array}{l}1=1-2t\\ 3=-2+t\end{array}\right.\iff \left\{\begin{array}{l}t=0\\ t=5\end{array}\right.$ (vô nghiệm)

Vậy điểm D(1; 3) không thuộc đường thẳng ∆.

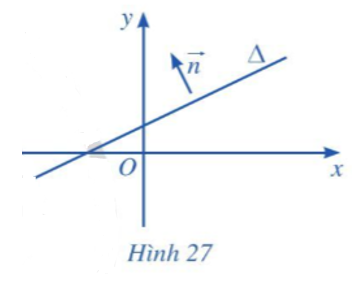
Hoạt động 3 trang 75 Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆. Vẽ vectơ $\overrightarrow{n}\left(\overrightarrow{n}\ne \overrightarrow{0}\right)$ có giá vuông góc với đường thẳng ∆ (Hình 27).

Lời giải

Giá của vectơ là đường thẳng đi qua 2 đầu mút của vectơ. Vậy ta vẽ như sau:

+ Vẽ một đoạn thẳng bất kì vuông góc với đường thẳng ∆.

+ Đánh dấu hướng mũi tên trên đoạn thẳng đó, ta được vectơ thỏa mãn yêu cầu bài toán.

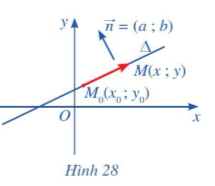
Hoạt động 4 trang 75 Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho đường thẳng ∆ đi qua điểm M₀(x₀; y₀) và có vectơ pháp tuyến $\overrightarrow{n}=\left(a;b\right)$. Xét điểm M(x; y) nằm trên ∆ (Hình 28).

a) Nhận xét về phương của hai vectơ $\overrightarrow{n}$ và $\overrightarrow{M_{0}M}$.

b) Tìm mối liên hệ giữa tọa độ của điểm M với tọa độ của điểm M₀ và tọa độ của vectơ pháp tuyến $\overrightarrow{n}$.

Lời giải

a) Đường thẳng ∆ đi qua hai điểm M₀ và M hay đường thẳng ∆ chính là đường thẳng MM₀. Khi đó giá của vectơ $\overrightarrow{M_{0}M}$ là đường thẳng ∆. (1)

Vectơ $\overrightarrow{n}$ là vectơ pháp tuyến của đường thẳng ∆ nên giá của vectơ $\overrightarrow{n}$ vuông góc với đường thẳng ∆. (2)

Từ (1) và (2) suy ra giá của vectơ $\overrightarrow{n}$ và giá của vectơ $\overrightarrow{M_{0}M}$ vuông góc với nhau.

Vậy hai vectơ hai vectơ $\overrightarrow{n}$ và $\overrightarrow{M_{0}M}$ không cùng phương.

b) Ta có: $\overrightarrow{M_{0}M}=\left(x-x_0;y-y_0\right),\overrightarrow{n}=\left(a;b\right)$.

Vì $\overrightarrow{M_{0}M}\perp \overrightarrow{n}$ nên $\overrightarrow{M_{0}M}.\overrightarrow{n}=0$

⇔ a(x – x₀) + b(y – y₀) = 0

⇔ ax + by – ax₀ – by₀ = 0.

Giải Toán 10 trang 76 Tập 2

Luyện tập 2 trang 76 Toán 10 Tập 2: Cho đường thẳng Δ có phương trình tổng quát là x – y + 1 = 0.

a) Chỉ ra tọa độ của một vectơ pháp tuyến và một vectơ chỉ phương của Δ.

b) Chỉ ra tọa độ của hai điểm thuộc Δ.

Lời giải

a) Đường thẳng ∆ có phương trình tổng quát là x – y + 1 = 0.

Suy ra đường thẳng ∆ có một vectơ pháp tuyến là $\overrightarrow{n}=\left(1;-1\right)$.

Do đó đường thẳng ∆ có một vectơ chỉ phương là $\overrightarrow{u}=\left(1;1\right)$.

b) Cho x = 0 thay vào phương trình đường thẳng ∆ ta được: 0 – y + 1 = 0 ⇔ y = 1.

Suy ra điểm A(0; 1) thuộc đường thẳng ∆.

Cho x = 1 thay vào phương trình đường thẳng ∆ ta được: 1 – y + 1 = 0 ⇔ y = 2.

Suy ra điểm B(1; 2) thuộc đường thẳng ∆.

Vậy hai điểm thuộc đường thẳng ∆ là A(0; 1) và B(1; 2).

Hoạt động 5 trang 76 Toán 10 Tập 2: Cho đường thẳng ∆ có phương trình tổng quát ax + by + c = 0 (a hoặc b khác 0). Nêu nhận xét về vị trí tương đối của đường thẳng ∆ với các trục tọa độ trong mỗi trường hợp sau:

a) b = 0 và a ≠ 0.

b) b ≠ 0 và a = 0.

c) b ≠ 0 và a ≠ 0.

Lời giải

a) Nếu b = 0 và a ≠ 0 thì phương trình đường thẳng ∆ trở thành ax + c = 0. Khi đó đường thẳng ∆ song song hoặc trùng với trục Oy và cắt trục Ox tại điểm $\left(-\frac{c}{a};0\right)$.

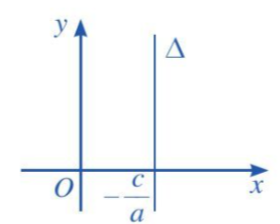
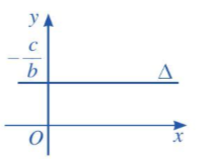
b) Nếu b ≠ 0 và a = 0 thì phương trình đường thẳng ∆ trở thành by + c = 0. Khi đó đường thẳng ∆ song song hoặc trùng với trục Ox và cắt trục Oy tại điểm $\left(0;-\frac{c}{b}\right)$.

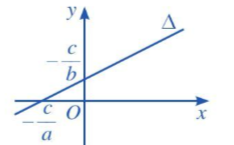
c) Nếu b ≠ 0 và a ≠ 0 thì phương trình đường thẳng ∆ có thể viết thành

$y=-\frac{a}{b}x-\frac{c}{b}$.

Khi đó, đường thẳng ∆ là đồ thị hàm số bậc nhất $y=-\frac{a}{b}x-\frac{c}{b}$ với hệ số góc là $k=-\frac{a}{b}$.

B. Bài tập

Giải Toán 10 trang 79 Tập 2

Bài 1 trang 79 Toán 10 Tập 2: Lập phương trình tổng quát của đường thẳng Δ đi qua điểm A(– 1; 2) và

a) Có vectơ pháp tuyến là $\overrightarrow{n}=\left(3;2\right)$.

b) Có vectơ chỉ phương là $\overrightarrow{u}=\left(-2;3\right)$.

Lời giải

a) Đường thẳng ∆ đi qua điểm A(– 1; 2) và có vectơ pháp tuyến là $\overrightarrow{n}=\left(3;2\right)$.

Do đó phương trình tổng quát của đường thẳng ∆ là:

3(x – (– 1)) + 2(y – 2) = 0 hay 3x + 2y – 1 = 0.

b) Đường thẳng ∆ có vectơ chỉ phương là $\overrightarrow{u}=\left(-2;3\right)$, suy ra ∆ có một vectơ pháp tuyến là $\overrightarrow{n}=\left(3;2\right)$.

Đường thẳng ∆ đi qua điểm A(– 1; 2) và có vectơ pháp tuyến là $\overrightarrow{n}=\left(3;2\right)$.

Do đó phương trình tổng quát của đường thẳng ∆ là:

3(x – (– 1)) + 2(y – 2) = 0 hay 3x + 2y – 1 = 0.

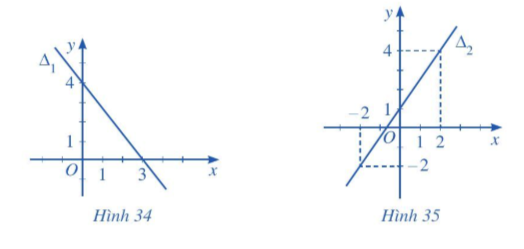
Bài 2 trang 79, 80 Toán 10 Tập 2: Lập phương trình mỗi đường thẳng trong các Hình 34, 35, 36, 37 sau đây:

Lời giải

+) Từ Hình 34 ta thấy đường thẳng ∆₁ đi qua hai điểm A(3; 0) và B(0; 4).

Ta có $\overrightarrow{AB}=\left(-3;4\right)$.

Đường thẳng ∆₁ đi qua điểm A và nhận $\overrightarrow{AB}$ làm vectơ chỉ phương, do đó phương trình tham số của đường thẳng ∆₁ là $\left\{\begin{array}{l}x=3-3t\\ y=4t\end{array}\right.$ (t là tham số).

+) Từ Hình 35 ta thấy đường thẳng ∆₂ đi qua hai điểm C(2; 4) và D(– 2; – 2).

Ta có: $\overrightarrow{DC}=\left(4;6\right)$.

Suy ra $\overrightarrow{u}=\frac{1}{2}\overrightarrow{DC}=\frac{1}{2}\left(4;6\right)=\left(2;3\right)$.

Đường thẳng ∆₂ đi qua điểm C và nhận $\overrightarrow{u}$ làm vectơ chỉ phương, do đó phương trình tham số của đường thẳng ∆₂ là $\left\{\begin{array}{l}x=2+2t\\ y=4+3t\end{array}\right.$ (t là tham số).

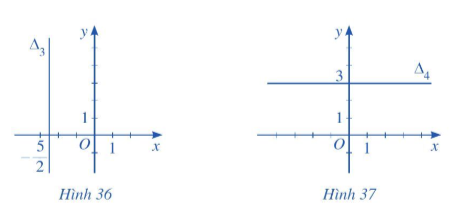
+) Từ Hình 36 ta thấy đường thẳng ∆₃ song song với trục Oy và cắt trục Ox tại điểm $M\left(-\frac{5}{2};0\right)$.

Do đó phương trình đường thẳng ∆₃ là $x=-\frac{5}{2}$ hay 2x + 5 = 0.

+) Từ Hình 37 ta thấy đường thẳng ∆₄ song song với trục Ox và cắt trục Oy tại điểm N(0; 3).

Do đó phương trình đường thẳng ∆₄ là y = 3 hay y – 3 = 0.

Giải Toán 10 trang 80 Tập 2

Bài 3 trang 80 Toán 10 Tập 2: Cho đường thẳng d có phương trình tham số là: $\left\{\begin{array}{l}x=-1-3t\\ y=2+2t\end{array}\right.$.

a) Lập phương trình tổng quát của đường thẳng d.

b) Tìm tọa độ giao điểm của đường thẳng d lần lượt với các trục Ox, Oy.

c) Đường thẳng d có đi qua điểm M(– 7; 5) hay không?

Lời giải

a) Đường thẳng d có phương trình tham số là: $\left\{\begin{array}{l}x=-1-3t\\ y=2+2t\end{array}\right.$.

Do đó, d có một vectơ chỉ phương là $\overrightarrow{u}=\left(-3;2\right)$.

Suy ra d có một vectơ pháp tuyến là $\overrightarrow{n}=\left(2;3\right)$.

Ứng với t = 0, thay vào phương trình tham số của d ta có: $\left\{\begin{array}{l}x=-1-3.0=-1\\ y=2+2.0=2\end{array}\right.$.

Do đó điểm A(– 1; 2) thuộc đường thẳng d.

Đường thẳng d đi qua điểm A(– 1; 2) và có một vectơ pháp tuyến là $\overrightarrow{n}=\left(2;3\right)$.

Vậy đường thẳng d có phương trình tổng quát là

2(x + 1) + 3(y – 2) = 0 hay 2x + 3y – 4 = 0.

b) Gọi E, F lần lượt là giao điểm của đường thẳng d với các trục Ox và Oy.

Vì E thuộc Ox nên tọa độ điểm E là E(a; 0).

Mà điểm E cũng thuộc d nên tọa độ điểm E thỏa mãn phương trình tổng quát của đường thẳng d nên thay (a; 0) vào phương trình đường thẳng d ta được:

2 . a + 3 . 0 – 4 = 0 ⇔ a = 2.

Do đó, E(2; 0).

Vì điểm F thuộc Oy nên tọa độ điểm F là F(0; b).

Mà điểm F thuộc d nên tọa độ điểm F thỏa mãn phương trình tổng quát của đường thẳng d nên thay (0; b) vào phương trình đường thẳng d ta được:

2 . 0 + 3 . b – 4 = 0 ⇔ b = $\frac{4}{3}$.

Do đó, $F\left(0;\frac{4}{3}\right)$.

Vậy tọa độ giao điểm của đường thẳng d lần lượt với các trục Ox, Oy lần lượt là các điểm E(2; 0) và $F\left(0;\frac{4}{3}\right)$.

c) Thay tọa độ điểm M(– 7; 5) vào phương trình tổng quát của đường thẳng d ta được:

2 . (– 7) + 3 . 5 – 4 = 0 ⇔ – 3 = 0 (vô lý).

Vậy đường thẳng d không đi qua điểm M(– 7; 5).

Bài 4 trang 80 Toán 10 Tập 2: Cho đường thẳng d có phương trình tổng quát là: x – 2y – 5 = 0.

a) Lập phương trình tham số của đường thẳng d.

b) Tìm tọa độ điểm M thuộc d sao cho OM = 5 với O là gốc tọa độ.

c) Tìm tọa độ điểm N thuộc d sao cho khoảng cách từ N đến trục hoành Ox là 3.

Lời giải

a) Đường thẳng d có phương trình tổng quát là: x – 2y – 5 = 0.

Suy ra d có một vectơ pháp tuyến là $\overrightarrow{n}=\left(1;-2\right)$.

Do đó d có một vectơ chỉ phương là $\overrightarrow{u}=\left(2;1\right)$.

Với y = 0 thay vào phương trình tổng quát của d ta được: x – 2 . 0 – 5 = 0 ⇔ x = 5.

Suy ra điểm A(5; 0) thuộc đường thẳng d.

Đường thẳng d đi qua điểm A(5; 0) và có một vectơ chỉ phương là $\overrightarrow{u}=\left(2;1\right)$.

Vậy phương trình tham số của đường thẳng d là $\left\{\begin{array}{l}x=5+2t\\ y=t\end{array}\right.$ (t là tham số).

b) Vì điểm M thuộc đường thẳng d nên ta gọi tọa độ điểm M(5 + 2t; t).

Với O là gốc tọa độ, ta có: $\overrightarrow{OM}=\left(5+2t;t\right)$, suy ra $OM=\left|\overrightarrow{OM}\right|=\sqrt{{\left(5+2t\right)}^2+t^2}$.

Theo bài ra ta có OM = 5.

Do đó: $\sqrt{{\left(5+2t\right)}^2+t^2}=5$

⇒ (5 + 2t)² + t² = 25 (bình phương cả hai vế)

⇔ 25 + 20t + 4t² + t² = 25

⇔ 5t² + 20t = 0

⇔ t² + 4t = 0

⇔ t(t + 4) = 0

⇔ t = 0 hoặc t = – 4.

+ Với t = 0 thì tọa độ M(5; 0).

+ Với t = – 4 thì tọa độ M(– 3; – 4).

Vậy M(5; 0) hoặc M(– 3; – 4) thì thỏa mãn yêu cầu bài toán.

c) Vì điểm N thuộc đường thẳng d nên gọi tọa độ điểm N(5 + 2t; t).

Gọi hình chiếu của N lên trục hoành Ox là E.

E thuộc trục hoành nên E có tung độ bằng 0 và E là hình chiếu của N lên Ox nên hoành độ của điểm E bằng hoành độ của điểm N.

Suy ra tọa độ của điểm E là E(5 + 2t; 0).

Khoảng cách từ N đến trục hoành Ox chính bằng đoạn thẳng NE.

Do đó NE = 3.

Ta có: $\overrightarrow{NE}=\left(0;-t\right)$

Suy ra $NE=\left|\overrightarrow{NE}\right|=\sqrt{0^2+{\left(-t\right)}^2}=\sqrt{t^2}=\left|t\right|$.

Do đó: |t| = 3, suy ra t = 3 hoặc t = – 3.

+ Với t = 3 thì N(11; 3).

+ Với t = – 3 thì N(– 1; – 3).

Vậy N(11; 3) hoặc N(– 1; – 3) thì thỏa mãn yêu cầu bài toán.

Bài 5 trang 80 Toán 10 Tập 2: Cho tam giác ABC, biết A(1; 3), B(– 1; – 1), C(5; – 3). Lập phương trình tổng quát của:

a) Ba đường thẳng AB, BC, AC;

b) Đường trung trực cạnh AB;

c) Đường cao AH và đường trung tuyến AM của tam giác ABC.

Lời giải

a) Ta có: $\overrightarrow{AB}=\left(\left(-1\right)-1;\left(-1\right)-3\right)$ nên $\overrightarrow{AB}=\left(-2;-4\right)$.

Đường thẳng AB nhận $\overrightarrow{u_{AB}}=-\frac{1}{2}\overrightarrow{AB}=-\frac{1}{2}\left(-2;–4\right)=\left(1;2\right)$ làm một vectơ chỉ phương.

Suy ra đường thẳng AB có một vectơ pháp tuyến là $\overrightarrow{n_{AB}}=\left(2;-1\right)$.

Vậy phương trình tổng quát của đường thẳng AB là

2(x – 1) – 1(y – 3) = 0 hay 2x – y + 1 = 0.

Ta có: $\overrightarrow{BC}=\left(5-\left(-1\right);\left(-3\right)-\left(-1\right)\right)$ nên $\overrightarrow{BC}=\left(6;-2\right)$.

Đường thẳng BC nhận $\overrightarrow{u_{BC}}=\frac{1}{2}\overrightarrow{BC}=\frac{1}{2}\left(6;–2\right)=\left(3;-1\right)$ làm một vectơ chỉ phương.

Suy ra đường thẳng BC có một vectơ pháp tuyến là $\overrightarrow{n_{BC}}=\left(1;3\right)$.

Vậy phương trình tổng quát của đường thẳng BC là

1(x + 1) + 3(y + 1) = 0 hay x + 3y + 4 = 0.

Ta có: $\overrightarrow{AC}=\left(5-1;\left(-3\right)-3\right)$ nên $\overrightarrow{AC}=\left(4;-6\right)$.

Đường thẳng AC nhận $\overrightarrow{u_{AC}}=\frac{1}{2}\overrightarrow{AB}=\frac{1}{2}\left(4;–6\right)=\left(2;-3\right)$ làm một vectơ chỉ phương.

Suy ra đường thẳng AC có một vectơ pháp tuyến là $\overrightarrow{n_{AC}}=\left(3;2\right)$.

Vậy phương trình tổng quát của đường thẳng AC là

3(x – 1) + 2(y – 3) = 0 hay 3x + 2y – 9 = 0.

b) Gọi E là trung điểm của AB.

Khi đó tọa độ của điểm E là $\left\{\begin{array}{l}{x}_E=\frac{x_A+x_B}{2}=\frac{1+\left(-1\right)}{2}=0\\ y_E=\frac{y_A+y_B}{2}=\frac{3+\left(-1\right)}{2}=1\end{array}\right.$ hay E(0; 1).

Đường trung trực cạnh AB vuông góc với AB nên nhận $\overrightarrow{u_{AB}}=\left(1;2\right)$ làm vectơ pháp tuyến.

Do đó đường trung trực cạnh AB đi qua điểm E(0; 1) và có vectơ pháp tuyến là $\overrightarrow{n}=\left(1;2\right).$

Vậy phương trình tổng quát của đường trung trực cạnh AB là

1(x – 0) + 2(y – 1) = 0 hay x + 2y – 2 = 0.

c) Đường cao AH của tam giác ABC vuông góc với cạnh BC.

Do đó đường cao AH đi qua điểm A(1; 3) và nhận $\overrightarrow{u_{BC}}=\left(3;-1\right)$ làm vectơ pháp tuyến.

Vậy phương trình tổng quát của đường cao AH là

3(x – 1) – 1(y – 3) = 0 hay 3x – y = 0.

Vì AM là trung tuyến của tam giác ABC nên M là trung điểm của BC.

Suy ra tọa độ của điểm M là $\left\{\begin{array}{l}{x}_M=\frac{x_B+x_C}{2}=\frac{\left(-1\right)+5}{2}=2\\ y_M=\frac{y_B+y_C}{2}=\frac{\left(-1\right)+\left(-3\right)}{2}=-2\end{array}\right.$ hay M(2; – 2).

Ta có: $\overrightarrow{AM}=\left(1;-5\right)$ là vectơ chỉ phương của đường trung tuyến AM.

Suy ra AM có một vectơ pháp tuyến là $\overrightarrow{n_{AM}}=\left(5;1\right)$.

Đường trung tuyến AM đi qua A(1; 3) và nhận $\overrightarrow{n_{AM}}=\left(5;1\right)$ làm vectơ pháp tuyến.

Vậy phương trình tổng quát của đường trung tuyến AM là

5(x – 1) + 1(y – 3) = 0 hay 5x + y – 8 = 0.

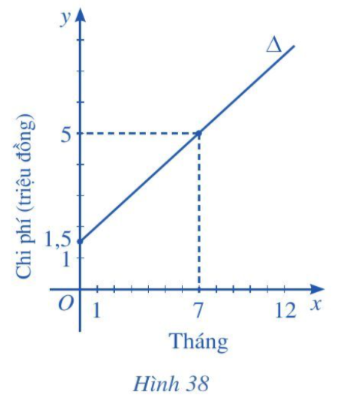
Bài 6 trang 80 Toán 10 Tập 2: Để tham gia một phòng tập thể dục, người tập phải trả một khoản phí tham gia ban đầu và phí sử dụng phòng tập. Đường thẳng Δ ở Hình 38 biểu thị tổng chi phí (đơn vị: triệu đồng) để tham gia một phòng tập thể dục theo thời gian tập của một người (đơn vị: tháng).

a) Viết phương trình của đường thẳng Δ.

b) Giao điểm của đường thẳng Δ với trục tung trong tình huống này có ý nghĩa gì?

c) Tính tổng chi phí mà người đó phải trả khi tham gia phòng tập thể dục với thời gian 12 tháng.

Lời giải

a) Từ Hình 38 ta thấy đường thẳng ∆ đi qua 2 điểm A(0; 1,5) và B(7; 5).

Ta có: $\overrightarrow{AB}=\left(7;\mathrm{3,5}\right)$.

Suy ra đường thẳng ∆ có một vectơ chỉ phương là $\overrightarrow{u}=\frac{2}{7}\overrightarrow{AB}=\frac{2}{7}\left(7;\mathrm{3,5}\right)=\left(2;1\right)$.

Vậy phương trình tham số của đường thẳng ∆ là $\left\{\begin{array}{l}x=2t\\ y=\mathrm{1,5}+t\end{array}\right.$ (t là tham số).

b) Giao điểm của đường thẳng ∆ với trục tung là điểm A(0; 1,5).

Giao điểm của đường thẳng Δ với trục tung trong tình huống này có ý nghĩa là khoản phí tham gia ban đầu mà người tập phải trả là 1,5 triệu đồng.

c) Người đó tham gia phòng tập thể dục với thời gian là 12 tháng hay x = 12.

Thay x = 12 vào phương trình tham số của đường thẳng ∆ ta được: $\left\{\begin{array}{l}12=2t\\ y=\mathrm{1,5}+t\end{array}\right.$

$\iff \left\{\begin{array}{l}t=6\\ y=\mathrm{1,5}+t\end{array}\right.\iff \left\{\begin{array}{l}t=6\\ y=\mathrm{1,5}+6\end{array}\right.\iff \left\{\begin{array}{l}t=6\\ y=\mathrm{7,5}\end{array}\right.$.

Do đó với x = 12 (tháng) thì y = 7,5 (triệu đồng).

Vậy tổng chi phí mà người đo phải trả khi tham gia phòng tập thể dục với thời gian 12 tháng là 7,5 triệu đồng.

Lý thuyết Toán 10 Bài 3: Phương trình đường thẳng - Cánh diều

I. Phương trình tham số của đường thẳng

1. Vectơ chỉ phương của đường thẳng

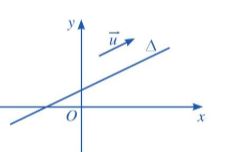
Vectơ $\overrightarrow{u}$ được gọi là vectơ chỉ phương của đường thẳng ∆ nếu $\overrightarrow{u}$ ≠ $\overrightarrow{0}$ và giá của $\overrightarrow{u}$ song song hoặc trùng với ∆.

Nhận xét:

– Nếu $\overrightarrow{u}$ là một vectơ chỉ phương của ∆ thì k$\overrightarrow{u}$ (k ≠ 0) cũng là một vectơ chỉ phương của ∆.

– Một đường thẳng hoàn toàn được xác định khi biết một điểm và một vectơ chỉ phương của đường thẳng đó.

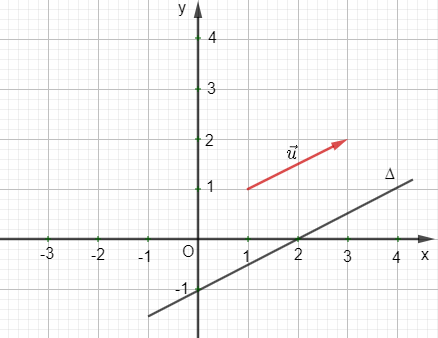
Ví dụ: Đường thẳng ∆ đi qua điểm (2 ; 0) và (0 ; –1) có vectơ chỉ phương $\overrightarrow{u}$ như hình vẽ sau:

2. Phương trình tham số của đường thẳng

Hệ $\left\{\begin{array}{l}x=x_0+at\\ y=y_0+bt\end{array}\right.$ (a² + b² > 0 và t là tham số) được gọi là phương trình tham số của đường thẳng ∆ đi qua M₀(x₀ ; y₀₎ và nhận $\overrightarrow{u}$ = (a ; b) làm vectơ chỉ phương.

Nhận xét: Cho đường thẳng ∆ có phương trình tham số là: $\left\{\begin{array}{l}x=x_0+at\\ y=y_0+bt\end{array}\right.$ (a² + b² > 0 và t là tham số).

+ Với mỗi giá trị cụ thể của t, ta xác định được một điểm trên đường thẳng ∆. Ngược lại, với mỗi điểm trên đường thẳng ∆, ta xác định được một giá trị cụ thể của t.

+ Vectơ $\overrightarrow{u}$ = (a ; b) là một vectơ chỉ phương của ∆.

Ví dụ:

a) Viết phương trình tham số của đường thẳng ∆ đi qua điểm A(1; 2) và có vectơ chỉ phương $\overrightarrow{u}$ = (–1 ; 3).

b) Cho đường thẳng ∆ có phương trình tham số là $\left\{\begin{array}{l}x=4+2t\\ y=-3-t\end{array}\right.$. Chỉ ra tọa độ một vectơ chỉ phương của ∆ và một điểm thuộc đường thẳng ∆.

Hướng dẫn giải

a) Phương trình đường thẳng ∆ đi qua điểm A(1; 2) và có vectơ chỉ phương $\overrightarrow{u}$ = (–1 ; 3) nên có phương trình tham số là $\left\{\begin{array}{l}x=1-t\\ y=2+3t\end{array}\right.$.

Vậy phương trình tham số của đường thẳng ∆ là $\left\{\begin{array}{l}x=1-t\\ y=2+3t\end{array}\right.$.

b) Đường thẳng ∆ có phương trình tham số là $\left\{\begin{array}{l}x=4+2t\\ y=-3-t\end{array}\right.$.

Khi đó ∆ có một vectơ chỉ phương là (2 ; –1) và điểm (4 ; –3) thuộc ∆.

Vậy ∆ có một vectơ chỉ phương là (2 ; –1) và điểm (4 ; –3) thuộc ∆.

II. Phương trình tổng quát của đường thẳng

1. Vectơ pháp tuyến của đường thẳng

Vectơ $\overrightarrow{n}$ được gọi là vectơ pháp tuyến của đường thẳng ∆ nếu $\overrightarrow{n}$ ≠ $\overrightarrow{0}$ và giá của vectơ $\overrightarrow{n}$ vuông góc với ∆.

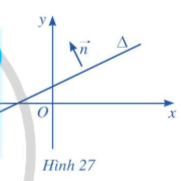
Nhận xét:

– Nếu $\overrightarrow{n}$ là một vectơ pháp tuyến của ∆ thì k$\overrightarrow{n}$ (k ≠ 0) cũng là một vectơ pháp tuyến của ∆.

– Một đường thẳng hoàn toàn được xác định khi biết một điểm và một vectơ pháp tuyến của đường thẳng đó.

– Nếu một đường thẳng ∆ có vectơ chỉ phương là $\overrightarrow{u}$ = (a ; b) thì vectơ $\overrightarrow{n}$ = (–b ; a) là một vectơ pháp tuyến của ∆.

2. Phương trình tổng quát của đường thẳng

Phương trình ax + by + c = 0 (a và b không đồng thời bằng 0) được gọi là phương trình tổng quát của đường thẳng.

Nhận xét:

– Đường thẳng ∆ đi qua điểm M_0­ (x₀ ; y₀) và nhận $\overrightarrow{n}$ = (a ; b) làm vectơ pháp tuyến có phương trình là: a(x – x₀) + b(y – y₀) = 0 ⇔ ax + by + (–ax₀ – by₀) = 0.

– Mỗi phương trình ax + by + c = 0 (a và b không đồng thời bằng 0) đều xác định một đường thẳng ∆ trong mặt phẳng tọa độ nhận một vectơ pháp tuyến là $\overrightarrow{n}$ = (a ; b).

Ví dụ: Viết phương trình tổng quát của đường thẳng d đi qua điểm A(1; –2) và có vectơ pháp tuyến $\overrightarrow{n}$ = (–2 ; –3).

Hướng dẫn giải

Theo giả thiết, phương trình của đường thẳng d là : –2(x – 1) + (–3).(y + 2) = 0.

Từ đó, ta nhận được phương trình tổng quát của đường thẳng d là –2x – 3y – 4 = 0.

Vậy phương trình tổng quát của d là –2x – 3y – 4 = 0.

3. Những dạng đặc biệt của phương trình tổng quát

Cho đường thẳng ∆ có phương trình tổng quát ax + by + c = 0 (a hoặc b khác 0).

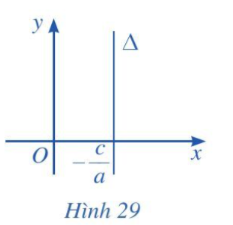
a) Nếu b = 0 và a ≠ 0 thì phương trình đường thẳng ∆ trở thành ax + c = 0. Khi đó đường thẳng ∆ song song hoặc trùng với trục Oy và cắt trục Ox tại điểm $\left(-\frac{c}{a};0\right)$.

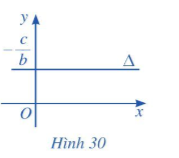
b) Nếu b ≠ 0 và a = 0 thì phương trình đường thẳng ∆ trở thành by + c = 0. Khi đó đường thẳng ∆ song song hoặc trùng với trục Ox và cắt trục Oy tại điểm $\left(0;-\frac{c}{b}\right)$ (Hình 30).

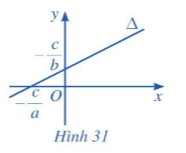
c) Nếu b ≠ 0 và a ≠ 0 thì phương trình đường thẳng ∆ có thể viết thành

y = $-\frac{a}{b}$x – $\frac{c}{b}$.

Khi đó, đường thẳng ∆ là đồ thị hàm số bậc nhất y = $-\frac{a}{b}$x – $\frac{c}{b}$ với hệ số góc là k = $-\frac{a}{b}$(Hình 31).

Nhận xét:

– Đường thẳng ∆ có phương trình tổng quát ax + by + c = 0 (a hoặc b khác 0) là đồ thị của hàm số bậc nhất khi và chỉ khi a ≠ 0 và b ≠ 0.

– Phương trình trục hoành là y = 0, phương trình trục tung là x = 0.

Ví dụ:

a) Cho phương trình đường thẳng ∆ là 2x + 4 = 0. Khi đó đường thẳng ∆ song song với trục Oy và cắt trục Ox tại điểm (–2 ; 0)

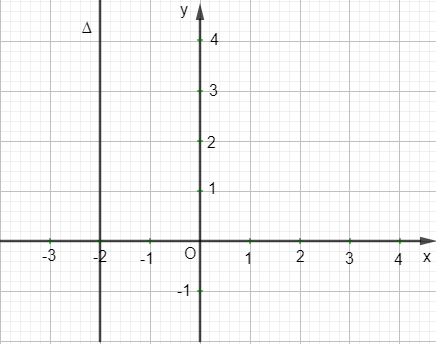
b) Cho phương trình đường thẳng ∆ là 3x – 9 = 0. Khi đó đường thẳng ∆ song song với trục Ox và cắt trục Oy tại điểm (0 ; 3)

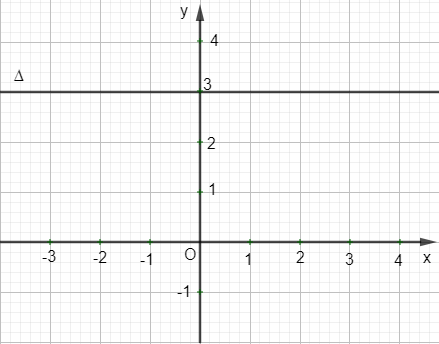
c) Cho phương trình đường thẳng ∆ là x + 2y – 2 = 0. Khi đó, đường thẳng ∆ là đồ thị của hàm số bậc nhất y = $-\frac{1}{2}$x + 1 với hệ số góc k = $-\frac{1}{2}$

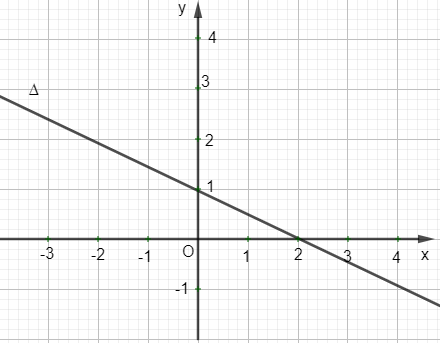
III. Lập phương trình đường thẳng

1. Lập phương trình đường thẳng đi qua một điểm và biết vectơ pháp tuyến

Phương trình đường thẳng ∆ đi qua điểm M₀(x₀ ; y₀) và nhận $\overrightarrow{n}$ = (a ; b) ($\overrightarrow{n}$ ≠ $\overrightarrow{0}$) làm vectơ pháp tuyến là a(x – x₀) + b(y – y₀) = 0.

Ví dụ: Lập phương trình của đường thẳng ∆ đi qua điểm M(2; –2) và có vectơ pháp tuyến $\overrightarrow{n}$ = (2 ; 3).

Hướng dẫn giải

Theo giả thiết, phương trình của đường thẳng ∆ là: 2(x – 2) + 3.(y + 2) = 0.

Từ đó, ta nhận được phương trình của đường thẳng ∆ là 2x + 3y + 2 = 0.

Vậy phương trình của ∆ là 2x + 3y + 2 = 0.

2. Lập phương trình đường thẳng đi qua một điểm và biết vectơ chỉ phương

Phương trình tham số của đường thẳng ∆ đi qua điểm M₀(x₀ ; y₀) và nhận $\overrightarrow{u}$ = (a ; b) ($\overrightarrow{u}$≠ $\overrightarrow{0}$) làm vectơ chỉ phương là $\left\{\begin{array}{l}x=x_0+at\\ y=y_0+bt\end{array}\right.$ (t là tham số).

Nếu a ≠ 0 và b ≠ 0 thì ta còn có thể viết phương trình của đường thẳng ∆ ở dạng: $\frac{x-x_0}{a}=\frac{y-y_0}{b}$.

Ví dụ: Viết phương trình tham số của đường thẳng ∆ đi qua điểm M(–1; 2) và có vectơ chỉ phương $\overrightarrow{u}$ = (1 ; –3).

Hướng dẫn giải

Cách 1: Phương trình tham số của đường thẳng ∆ đi qua điểm M(–1; 2) và có vectơ chỉ phương $\overrightarrow{u}$ = (1 ; –3) là $\left\{\begin{array}{l}x=-1+t\\ y=2-3t\end{array}\right.$.

Vậy phương trình tham số của đường thẳng ∆ là $\left\{\begin{array}{l}x=-1+t\\ y=2-3t\end{array}\right.$.

Cách 2: Phương trình đường thẳng ∆ đi qua điểm M(–1; 2) và có vectơ chỉ phương $\overrightarrow{u}$ = (1 ; –3) nên có phương trình là $\frac{x+1}{1}=\frac{y-2}{-3}$ ⇔ –3x – y – 1= 0.

Vậy phương trình của đường thẳng ∆ là –3x – y – 1= 0.

3. Lập phương trình đi qua hai điểm

Đường thẳng ∆ đi qua hai điểm A(x₀ ; y₀), B(x₁ ; y₁) nên nhận vectơ $\overrightarrow{AB}$ = (x₁ – x₀ ; y₁ – y₀) làm vectơ chỉ phương. Do đó, phương trình tham số của đường thẳng ∆ là: $\left\{\begin{array}{l}x=x_0+(x_1-x_0)t\\ y=y_0+(y_1-y_0)t\end{array}\right.$ (t là tham số).

Nếu x₁ – x₀ ≠ 0 và y₁ – y₀ ≠ 0 thì ta còn có thể viết phương trình của đường thẳng ∆ ở dạng: $\frac{x-x_0}{x_1-x_0}=\frac{y-y_0}{y_1-y_0}$.

Ví dụ: Lập phương trình ∆ đi qua hai điểm A(2 ; 2) và B(–1 ; 3).

Hướng dẫn giải

Phương trình ∆ đi qua hai điểm A(2 ; 2) và B(–1 ; 3) là

$\frac{x-2}{-1-2}=\frac{y-2}{3-2}$ ⇔ $\frac{x-2}{-3}=\frac{y-2}{1}$ ⇔ x + 3y – 8 = 0.

Vậy phương trình đường thẳng ∆ đi qua hai điểm A(2 ; 2) và B(–1 ; 3) là x + 3y – 8 = 0.

Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng

Bài 5: Phương trình đường tròn

Bài 6: Ba đường conic

Bài tập cuối chương 7

Chủ đề 2: Xây dựng mô hình hàm số bậc nhất, bậc hai biểu diễn số liệu dạng bảng