Giải Toán 10 Bài 2 (Cánh diều): Giải tam giác. Tính diện tích tam giác

Giải bài tập Toán 10 Bài 2: Giải tam giác. Tính diện tích tam giác

Giải Toán 10 trang 72 Tập 1

Câu hỏi khởi động trang 72 Toán lớp 10 Tập 1: Từ xa xưa, con người đã cần đo đạc các khoảng cách mà không thể trực tiếp đo được. Chẳng hạn, để do khoảng cách từ vị trí A trên bờ biển tới một hòn đảo (hay con tàu,…) trên biển, người xưa đã tìm ra một cách đo khoảng cách đó như sau:

Từ vị trí A, đo góc nghiêng α so với bờ biển tới một vị trí C quan sát được trên đảo. Sau đó di chuyển dọc bờ biển đến vị trí B cách A một khoảng d và tiếp tục đo góc nghiêng β so với bờ biển tới vị trí C đã chọn (Hình 18). Bằng cách giải tam giác BAC, họ tính được khoảng cách AC.

Giải tam giác được hiểu như thế nào?

Lời giải:

Giải tam giác là tính các cạnh và các góc của tam giác dựa trên những dữ kiện cho trước.

Hoạt động 1 trang 72 Toán lớp 10 Tập 1: Cho tam giác ABC có AB = c, AC = b, $\widehat{A}=\alpha$. Viết công thức tính BC theo b, c, α.

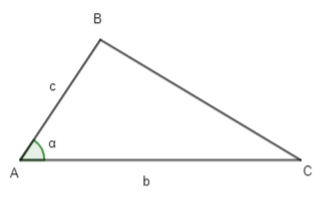
Lời giải:

Áp dụng định lí côsin vào tam giác ABC ta có:

BC² = AB² + AC² – 2.AB.AC.cos A = c² + b² – 2.b.c.cosα

$\Rightarrow BC=\sqrt{c^2+b^2-2bc\cos \alpha }$.

Giải Toán 10 trang 73 Tập 1

Hoạt động 2 trang 73 Toán lớp 10 Tập 1: Cho tam giác ABC có AB = c, AC = b, BC = a. Viết công thức tính cos A theo a, b, c.

Lời giải:

Áp dụng định lí côsin vào tam giác ABC ta có:

BC² = AB² + AC² - 2.AB.AC.cos A

$\Rightarrow$ cos A = $\frac{A{B}^2+A{C}^2-B{C}^2}{2.AB.AC}$

Vậy cos A = $\frac{A{B}^2+A{C}^2-B{C}^2}{2.AB.AC}$.

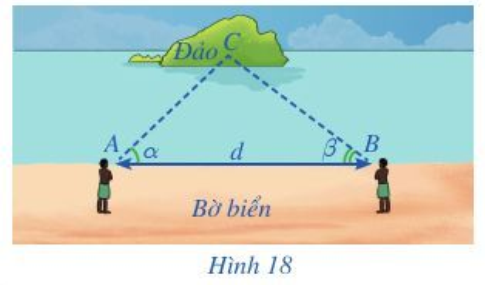
Hoạt động 3 trang 73 Toán lớp 10 Tập 1: Cho tam giác ABC có BC = a, $\widehat{B}=\alpha$, $\widehat{C}=\beta$. Viết công thức tính AB và AC theo a, α, β

Lời giải:

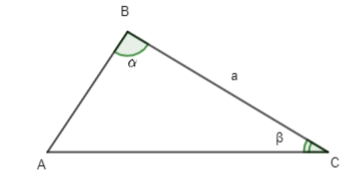
Trong tam giác ABC có: $\widehat{A}=180°-\widehat{B}-\widehat{C}=180°-\alpha -\beta$.

Áp dụng định lí sin vào tam giác ABC ta có:

$\frac{BC}{\sin A}=\frac{AC}{\sin B}=\frac{AB}{\sin C}$

$\Rightarrow \frac{a}{\sin \left(180°-\alpha -\beta \right)}=\frac{AC}{\sin \alpha }=\frac{AB}{\sin \beta }$

Do đó AC = $\frac{a.\sin \alpha }{\sin \left(180°-\alpha -\beta \right)}$ và AB = $\frac{a.\sin \beta }{\sin \left(180°-\alpha -\beta \right)}$.

Hoạt động 4 trang 73 Toán lớp 10 Tập 1: Cho tam giác ABC có AB = c, AC = b, BC = a. Kẻ đường cao BH.

a) Tính BH theo c và sin A.

b) Tính diện tích S của tam giác ABC theo b, c, và sin A.

Lời giải:

a) Xét các trường hợp:

+ Với $\widehat{A}<90°$

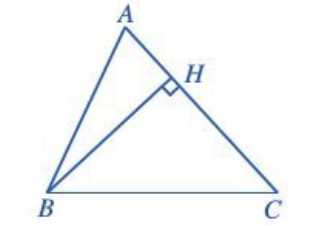
Xét tam giác vuông AHB, ta có $\sin \text{A}=\frac{BH}{BA}$

Do đó BH = AB . sin A = c . sin A.

+ Với $\widehat{A}=90°$

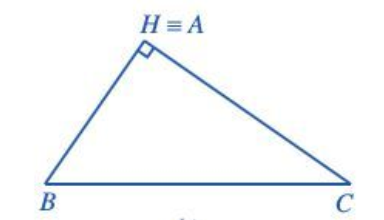
Khi đó sin A = sin 90^o = 1; BH = BA = c . 1 = c . sin A.

+ Với $\widehat{A}>90°$

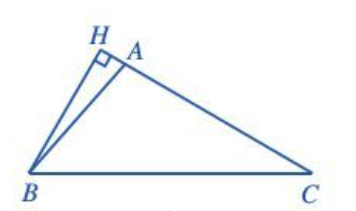
Xét tam giác AHB vuông, ta có: $\widehat{BAH}=180°-\widehat{A}$.

Do đó BH = AB . sin(180° – $\widehat{A}$) = AB . sin A = c . sin A.

Như vậy, trong mọi trường hợp ta đều có BH = c . sin A.

b) Diện tích tam giác ABC bằng $\frac{1}{2}$AC.BH nên $S=\frac{1}{2}AC.BH=\frac{1}{2}bc\sin A$.

Giải Toán 10 trang 74 Tập 1

Luyện tập 1 trang 74 Toán lớp 10 Tập 1: Cho tam giác ABC có AB = 12; $\widehat{B}=60°;\widehat{C}=45°$. Tính diện tích của tam giác ABC.

Lời giải:

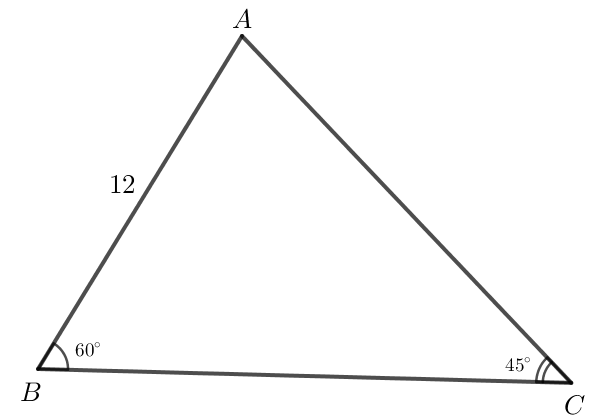
Xét tam giác ABC ta có $\widehat{A}=180°-\widehat{B}-\widehat{C}=180°-60°-45°=75°$.

Áp dụng định lí sin vào tam giác ABC ta có:

$\frac{BC}{\sin \text{A}}=\frac{AB}{\sin C}$

$\Rightarrow \frac{BC}{\sin 75°}=\frac{12}{\sin 45°}$

$\Rightarrow BC=\frac{12}{\sin 45°}.\sin 75°$

$\Rightarrow$ BC = 6 + $6\sqrt{3}$

Khi đó diện tích tam giác ABC bằng:

$\frac{1}{2}$AB . BC . sin B = $\frac{1}{2}$. 12 . (6 + $6\sqrt{3}$) . sin 60^o ≈ 85,2.

Giải Toán 10 trang 75 Tập 1

Hoạt động 5 trang 75 Toán lớp 10 Tập 1: Cho tam giác ABC có BC = a, CA = b, AB = c và diện tích S (Hình 24).

a) Từ định lí côsin, chứng tỏ rằng:

$\sin A=\frac{2}{bc}\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}$, ở đó $p=\frac{a+b+c}{2}$.

b) Bằng cách sử dụng công thức $S=\frac{1}{2}bc\sin A$, hãy chứng tỏ rằng:

$S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}$.

Lời giải:

a) Xét tam giác ABC, ta có:

BC² = AB² + AC² - 2.AB.AC.cos A (định lí cosin)

$\Rightarrow$ cos A = $\frac{A{B}^2+A{C}^2-B{C}^2}{2.AB.AC}$

$\Rightarrow$ cos A = $\frac{c^2+b^2-a^2}{2.c.b}$

$\Rightarrow {\cos }^{2}A=\frac{{\left(b^2+c^2-a^2\right)}^2}{4b^2{c}^2}$

Do $\widehat{A}$ là góc của tam giác ABC nên $0°<\widehat{A}<180°$.

Do đó sin A > 0.

Lại có cos² A + sin² A = 1 nên sin² A = 1 - cos² A.

$\Rightarrow {\sin }^{2}A=1-\frac{{\left(b^2+c^2-a^2\right)}^2}{4b^2{c}^2}$

$\Rightarrow {\sin }^{2}A=\frac{4b^2{c}^2-{\left(b^2+c^2-a^2\right)}^2}{4b^2{c}^2}$

$\Rightarrow {\sin }^{2}A=\frac{\left(2bc+b^2+c^2-a^2\right)\left(2bc-b^2-c^2+a^2\right)}{4b^2{c}^2}$

$\Rightarrow {\sin }^{2}A=\frac{\left[{\left(b+c\right)}^2-a^2\right]\left[a^2-{\left(b-c\right)}^2\right]}{4b^2{c}^2}$

$\Rightarrow {\sin }^{2}A=\frac{\left(b+c+a\right)\left(b+c-a\right)\left(a+b-c\right)\left(a-b+c\right)}{4b^2{c}^2}$

mà $p=\frac{a+b+c}{2}$

$\Rightarrow$ ${\sin }^{2}A=\frac{2p.2\left(p-a\right).2\left(p-c\right).2\left(p-b\right)}{4b^2{c}^2}$

$\Rightarrow {\sin }^{2}A=\frac{4p\left(p-a\right)\left(p-b\right)\left(p-c\right)}{b^2{c}^2}$

Do sin A > 0 nên $\sin A=\sqrt{\frac{4p\left(p-a\right)\left(p-b\right)\left(p-c\right)}{b^2{c}^2}}$.

Do đó $\sin A=\frac{2}{bc}\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}$.

b) Ta có diện tích tam giác ABC: S = $\frac{1}{2}$bc.sin A.

Mà $\sin A=\frac{2}{bc}\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}$ nên S = $\frac{1}{2}$bc. $\frac{2}{bc}\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}$.

Do đó $S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}$.

Giải Toán 10 trang 76 Tập 1

Luyện tập 2 trang 76 Toán lớp 10 Tập 1: Từ trên nóc của một tòa nhà cao 18,5 m, bạn Nam quan sát một cái cây cách tòa nhà 30 m và dùng giác kế đo được góc lệch giữa phương quan sát gốc cây và phương nằm ngang là 34°, góc lệch giữa phương quan sát ngọn cây và phương nằm ngang là 24°. Biết chiều cao của chân giác kế là 1,5 m. Chiều cao của cái cây là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?

Lời giải:

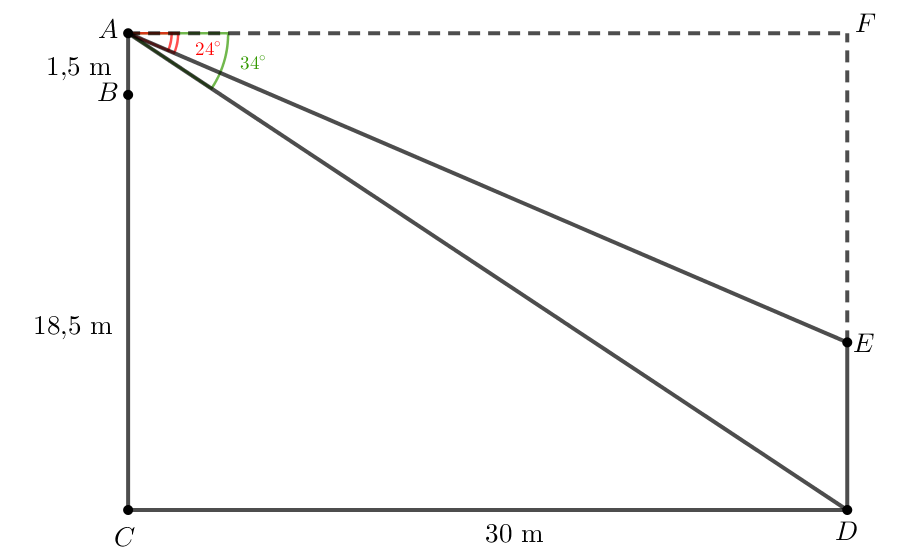
Gọi BC là chiều cao của tòa nhà, AB là chiều cao của chân giác kế, CD là khoảng cách giữa tòa nhà và cái cây, $\widehat{DAF}$ là góc lệch giữa phương quan sát gốc cây và phương nằm ngang, $\widehat{EAF}$ là góc lệch giữa ngọn cây và phương nằm ngang. Khi đó chiều cao của cây là độ dài DE.

Tam giác AFD vuông tại F nên $\tan \widehat{DAF}=\frac{DF}{AF}$

$\Rightarrow$ DF = AF . tan $\widehat{DAF}$ = 30 . tan 34^o ≈ 20,2 m.

Tam giác AFE vuông tại F nên $\tan \widehat{EAF}=\frac{EF}{AF}$

$\Rightarrow$ EF = AF. tan $\widehat{EAF}$ = 30 . tan 24^o ≈ 13,4 m.

Khi đó DE = DF - EF = 20,2 - 13,4 = 6,8 m.

Vậy chiều cao cây khoảng 6,8 m.

Bài tập

Giải Toán 10 trang 77 Tập 1

Bài 1 trang 77 Toán lớp 10 Tập 1: Cho tam giác ABC có BC = 12, CA = 15, $\widehat{C}=120°$. Tính:

a) Độ dài cạnh AB;

b) Số đo các góc A, B;

c) Diện tích tam giác ABC.

Lời giải:

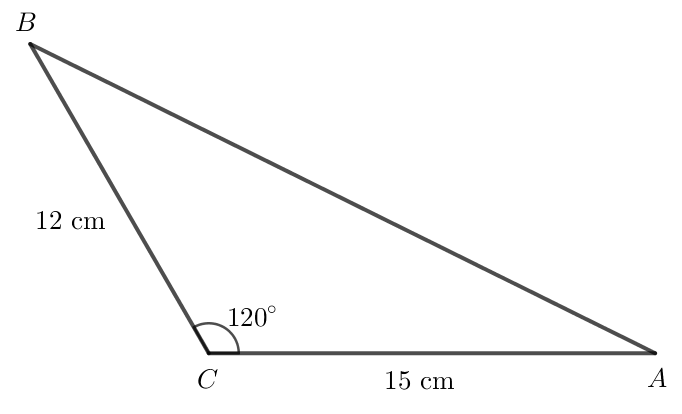
a) Áp dụng định lí côsin vào tam giác ABC có:

AB² = BC² + CA² - 2.BC.CA.cos C

$\Rightarrow$ AB² = 12² + 15² - 2.12.15.cos 120^o

$\Rightarrow$ AB² = 549

$\Rightarrow$ AB = $3\sqrt{61}$ m.

b) Áp dụng định lí sin vào tam giác ABC có:

$\frac{AB}{\sin C}=\frac{AC}{\sin B}$

$\Rightarrow \sin B=\frac{AC.\sin C}{AB}=\frac{15.\sin 120°}{3\sqrt{61}}\approx 0,554$

$\Rightarrow \widehat{B}$ ≈ 34^o.

Trong tam giác ABC có

$$\begin{gathered} \widehat{A}=180°-\widehat{B}-\widehat{C} \\ =180°-34°-120° \\ =26° \end{gathered}$$.

c) Diện tích tam giác ABC là:

S = $\frac{1}{2}$BC.AC.sin C = $\frac{1}{2}$.12.15.sin 120^o = $45\sqrt{3}$ (đvdt).

Bài 2 trang 77 Toán lớp 10 Tập 1: Cho tam giác ABC có AB = 5, BC = 7, $\widehat{A}=120°$. Tính độ dài cạnh AC.

Lời giải:

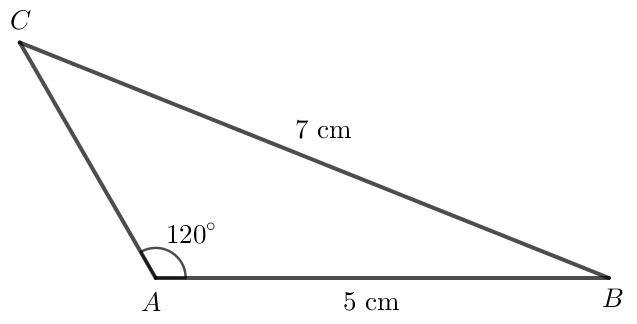
Áp dụng định lí sin vào tam giác ABC có:

$\frac{BC}{\sin \text{A}}=\frac{AB}{\sin C}$

$\Rightarrow \sin C=\frac{AB.\sin \text{A}}{BC}=\frac{5.\sin 120°}{7}=\frac{5\sqrt{3}}{14}$

$\Rightarrow \widehat{C}$ ≈ 38,2^o.

Trong tam giác ABC có

$$\begin{gathered} \widehat{B}=180°-\widehat{A}-\widehat{C} \\ =180°-120°-38,2° \\ =21,8° \end{gathered}$$.

Áp dụng định lí sin vào tam giác ABC có:

$\frac{BC}{\sin \text{A}}=\frac{AC}{\sin B}$

$\Rightarrow AC=\frac{BC.\sin B}{\sin \text{A}}=\frac{7.\sin 21,2°}{\sin 120°}\approx 2,9$ m.

Vậy độ dài cạnh AC là 2,9m.

Bài 3 trang 77 Toán lớp 10 Tập 1: Cho tam giác ABC có AB = 100, $\widehat{B}=100°$, $\widehat{C}=45°$. Tính:

a) Độ dài các cạnh AC, BC;

b) Diện tích tam giác ABC.

Lời giải:

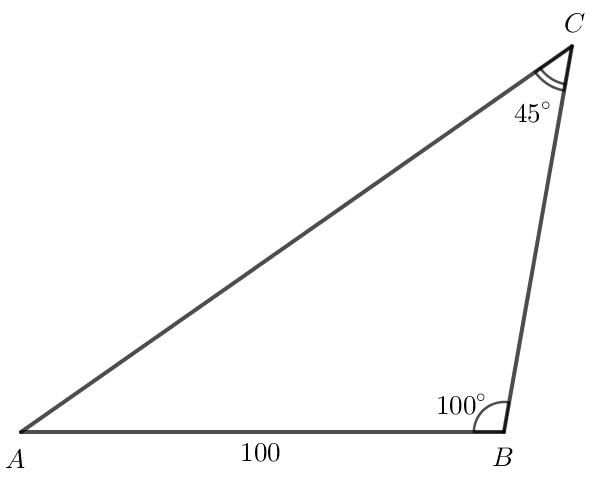
a) Trong tam giác ABC có

$$\begin{gathered} \widehat{A}=180°-\widehat{B}-\widehat{C} \\ =180°-100°-45° \\ =35° \end{gathered}$$.

Áp dụng định lí sin vào tam giác ABC có:

$\frac{AC}{\sin B}=\frac{AB}{\sin C}=\frac{BC}{\sin \text{A}}$

Do đó

$AC=\frac{AB.\sin B}{\sin C}=\frac{100.\sin 100°}{\sin 45°}\approx 139,3$;

$BC=\frac{AB.\sin \text{A}}{\sin C}=\frac{100.\sin 35°}{\sin 45°}\approx 81,1$.

Vậy AC ≈ 139,3, BC ≈ 81,1.

b) Diện tích tam giác ABC là:

S = $\frac{1}{2}$. AB.AC.sin A = $\frac{1}{2}$. 100 . 139,3 . sin 35^o ≈ 3995 (đvdt).

Vậy diện tích tam giác ABC là 3995 (đvdt).

Bài 4 trang 77 Toán lớp 10 Tập 1: Cho tam giác ABC có AB = 12, AC = 15, BC = 20. Tính:

a) Số đo các góc A, B, C;

b) Diện tích tam giác ABC.

Lời giải:

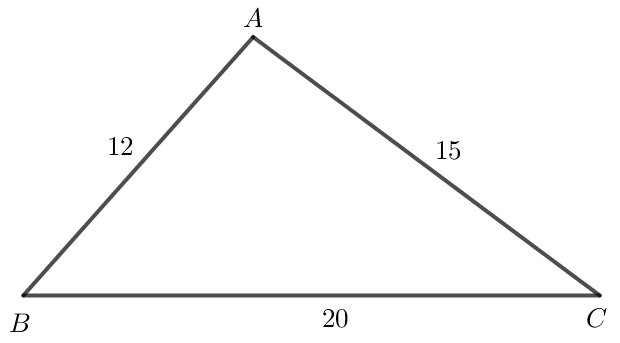
a) Áp dụng hệ quả của định lí côsin vào tam giác ABC ta có:

cos A = $\frac{A{B}^2+A{C}^2-B{C}^2}{2.AB.AC}=\frac{{12}^2+{15}^2-{20}^2}{\mathrm{2.12.15}}=\frac{-31}{360}$

$\Rightarrow \widehat{A}$ ≈ 95^o.

cos B = $\frac{B{C}^2+B{A}^2-A{C}^2}{2.BC.CA}=\frac{{20}^2+{12}^2-{15}^2}{\mathrm{2.20.12}}=\frac{319}{480}$

$\Rightarrow \widehat{B}$ ≈ 48^o.

Trong tam giác ABC có:

$$\begin{gathered} \widehat{C}=180°-\widehat{A}-\widehat{B} \\ =180°-95°-48°=37° \end{gathered}$$

b) Diện tích tam giác ABC là:

S = $\frac{1}{2}$AB . AC . sin A = $\frac{1}{2}$. 12 . 15 . sin 95^o ≈ 90 (đvdt).

Vậy diện tích tam giác ABC là 90 (đvdt).

Bài 5 trang 77 Toán lớp 10 Tập 1: Tính độ dài cạnh AB trong mỗi trường hợp sau:

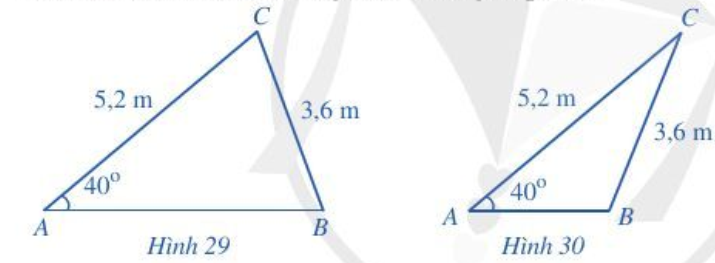
Lời giải:

+) Xét Hình 29:

Áp dụng định lí sin vào tam giác ABC ta có:

$\frac{BC}{\sin \text{A}}=\frac{AC}{\sin B}$

$\Rightarrow \sin B=\frac{AC.\sin \text{A}}{BC}=\frac{5,2.\sin 40°}{3,6}\approx 0,93$

$\Rightarrow \widehat{B}\approx 68°$.

Trong tam giác ABC có $\widehat{C}=180°-\widehat{A}-\widehat{B}=180°-40°-68°=72°$.

Áp dụng định lí sin vào tam giác ABC ta có:

$\frac{BC}{\sin \text{A}}=\frac{AB}{\sin C}$

$\Rightarrow AB=\frac{BC.\sin C}{\sin \text{A}}=\frac{3,6.\sin 72°}{\sin 40°}\approx 5,3$ m.

Vậy AB ≈ 5,3 m.

+) Xét Hình 30:

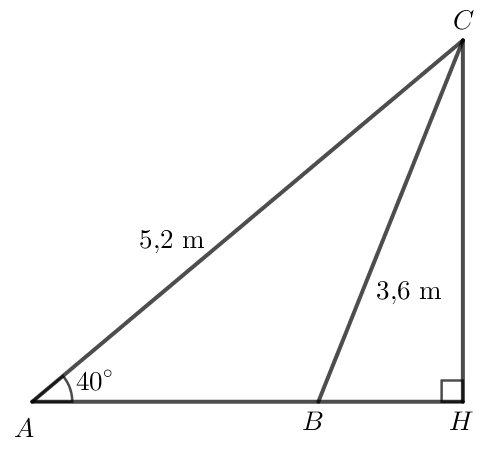
Gọi H là chân đường cao kẻ từ C đến AB.

Tam giác ACH vuông tại H nên $\text{cos\hspace{0.17em}}\widehat{CAH}=\frac{AH}{AC}$.

Do đó AH = AC. cos $\widehat{CAH}$ = 5,2 . cos 40^o ≈ 4 m.

$\text{sin\hspace{0.17em}}\widehat{CAH}=\frac{CH}{AC}\Rightarrow$ CH = AC . sin $\widehat{CAH}$ = 5,2 . sin 40^o ≈ 3,3 m.

Áp dụng định lí Pythagore vào tam giác BCH vuông tại H:

BH² + CH² = BC² $\Rightarrow$ BH² = BC² - CH²

$\Rightarrow$ BH² = 3,6² - 3,3² $\Rightarrow$ BH² = 2,07

$\Rightarrow$ BH ≈ 1,44 m.

Khi đó AB ≈ 4 - 1,44 ≈ 2,56 m.

Vậy AB ≈ 2,56m.

Bài 6 trang 77 Toán lớp 10 Tập 1: Để tính khoảng cách giữa hai địa điểm A và B mà không thể đi trực tiếp từ A đến B (hai địa điểm nằm ở hai bên bờ một hồ nước, một đầm lầy, …), người ta tiến hành như sau: Chọn một địa điểm C sao cho ta đo được các khoảng cách AC, CB và góc ACB. Sau khi đo, ta nhận được: AC = 1 km, CB = 800 m và $\widehat{ACB}=105°$ (Hình 31). Tính khoảng cách AB (làm tròn kết quả đến hàng phần mười theo đơn vị mét).

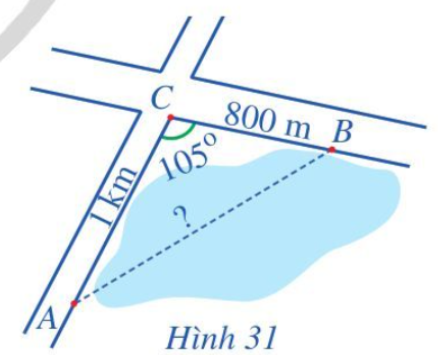
Lời giải:

Đổi 1 km = 1 000 m.

Ba vị trí A, B, C tạo thành ba đỉnh của tam giác.

Áp dụng định lí côsin vào tam giác ABC ta có:

AB² = AC² + BC² - 2.AC.BC.cos C

$\Rightarrow$ AB² = 1 000² + 800² - 2.1000.800.cos 105^o

$\Rightarrow$ AB² ≈ 2 054 110,5 m.

$\Rightarrow$ AB ≈ 1433,2 m.

Vậy AB ≈ 1433,2 m.

Bài 7 trang 77 Toán lớp 10 Tập 1: Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là 45° và 75°. Biết khoảng cách giữa hai bị trí A, B là 30 m (Hình 32). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?

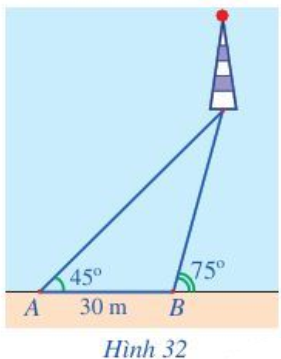
Lời giải:

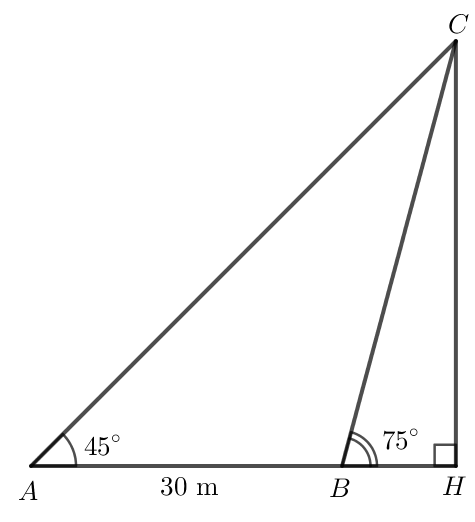
Gọi C là vị trí ngọn hải đăng, khi đó CH là khoảng cách giữa ngọn hải đăng và bờ.

Ta có $\widehat{CBH}$ là góc ngoài tại đỉnh B của tam giác ABC nên $\widehat{CBH}=\widehat{BAC}+\widehat{BCA}$.

Do đó $\widehat{BCA}=\widehat{CBH}-\widehat{BAC}=75°-45°=30°$.

Áp dụng định lí sin vào tam giác ABC có:

$\frac{AB}{\sin C}=\frac{BC}{\sin \text{A}}$

$\Rightarrow BC=\frac{AB.\sin \text{A}}{\sin C}=\frac{30.\sin 45°}{\sin 30°}=30\sqrt{2}$ m.

Trong tam giác CBH vuông tại H:

$\sin \widehat{CBH}=\frac{CH}{BC}$

$\Rightarrow$ CH = BC . sin $\widehat{CBH}$

= $30\sqrt{2}$ . sin 75^o = 15 + $15\sqrt{3}$ m ≈ 41 m.

Vậy khoảng cách từ ngọn hải đăng đến bờ khoảng 41 m.

Lý thuyết Toán 10 Bài 2. Giải tam giác. Tính diện tích tam giác – Cánh diều

1. Giải tam giác

Như ta đã biết, một tam giác hoàn toàn xác định nếu biết một trong những dữ kiện sau:

– Biết độ dài hai cạnh và độ lớn góc xen giữa hai cạnh đó;

– Biết độ dài ba cạnh;

– Biết độ dài một cạnh và độ lớn hai góc kề với cạnh đó.

Giải tam giác là tính các cạnh và các góc của tam giác dựa trên những dữ kiện cho trước.

Ví dụ: Cho tam giác ABC có AB = 4, BC = 6, AC = $2\sqrt{7}$. Điểm M thuộc đoạn BC sao cho MC = 2MB.

a) Tính cos các góc của tam giác ABC.

b) Tính độ dài cạnh AM.

Hướng dẫn giải:

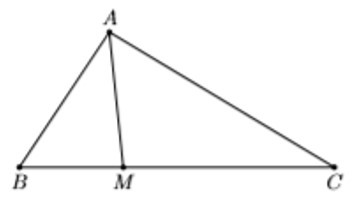
a) Theo định lí cosin trong tam giác ABC ta có:

cosB = $\frac{{\mathrm{AB}}^2+{\mathrm{BC}}^2-{\mathrm{AC}}^2}{2\mathrm{AB}.\mathrm{BC}}$= $\frac{4^2+6^2-{\left(2\sqrt{7}\right)}^2}{\mathrm{2.4.6}}$= $\frac{1}{2}$

⇒ $\widehat{\mathrm{B}}$= 60°.

cosC = $\frac{{\mathrm{AC}}^2+{\mathrm{BC}}^2-{\mathrm{AB}}^2}{2\mathrm{AC}.\mathrm{BC}}$= $\frac{{\left(2\sqrt{7}\right)}^2+6^2-4^2}{2.2\sqrt{7}.6}$= $\frac{2\sqrt{7}}{7}$

cosA = $\frac{{\mathrm{AB}}^2+{\mathrm{AC}}^2-{\mathrm{BC}}^2}{2\mathrm{AB}.\mathrm{AC}}$= $\frac{4^2+{\left(2\sqrt{7}\right)}^2-6^2}{\mathrm{2.4.2}\sqrt{7}}$= $\frac{\sqrt{7}}{14}$

b) Ta có:

MC = 2MB ⇒ $\frac{\mathrm{MB}}{\mathrm{MC}}$= $\frac{1}{2}$⇒ $\frac{\mathrm{MB}}{\mathrm{BC}}$= $\frac{1}{3}$

⇒ MB = $\frac{1}{3}$BC = $\frac{1}{3}$.6 = 2

Áp dụng định lí côsin trong tam giác AMB ta có:

AM² = AB² + BM² – 2AB.BM.cosB = 4² + 2² – 2.4.2. $\frac{1}{2}$= 12

⇒ AM = $\sqrt{12}$= $2\sqrt{3}$

Ví dụ: Cho tam giác ABC có $\widehat{\mathrm{B}}=35°$; $\widehat{\mathrm{C}}=50°$ và cạnh AC = 15 cm. Tính các cạnh còn lại của tam giác ABC (làm tròn đến chữ số thập phân thứ 2).

Hướng dẫn giải:

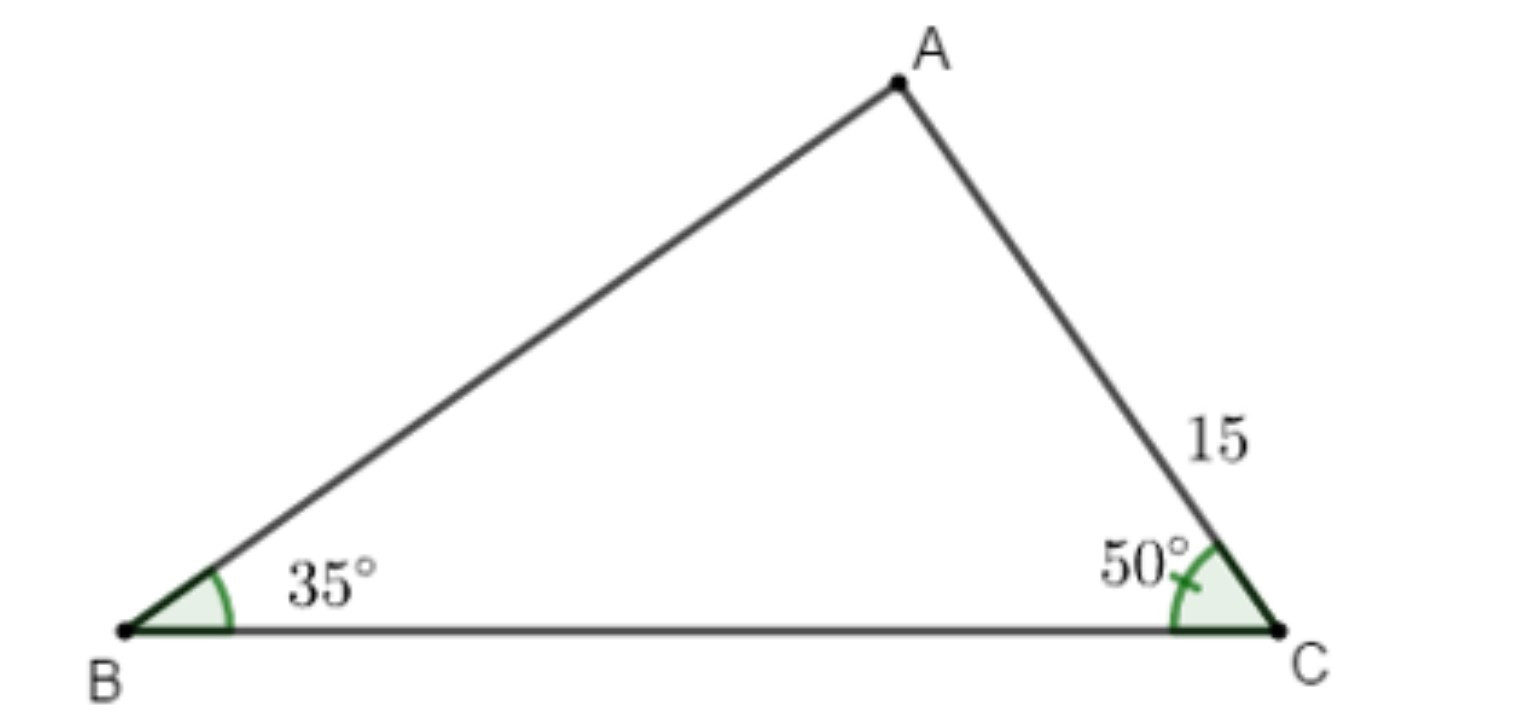
Ta có:

$\widehat{\mathrm{A}}$ + $\widehat{\mathrm{B}}$ + $\widehat{\mathrm{C}}$= 180° (tổng ba góc trong tam giác)

Suy ra:

$\widehat{\mathrm{A}}$ = 180° – $\widehat{\mathrm{B}}$ – $\widehat{\mathrm{C}}$ = 180° – 35° – 50° = 95°

Áp dụng định lí sin trong tam giác ABC ta có:

$\frac{\mathrm{BC}}{\mathrm{sinA}}$ = $\frac{\mathrm{AC}}{\mathrm{sinB}}$ = $\frac{\mathrm{AB}}{\mathrm{sinC}}$

Suy ra:

BC = $\frac{\mathrm{AC}.\mathrm{sinA}}{\mathrm{sinB}}$= $\frac{15.\sin 95°}{\sin 35°}$≈ 26,05cm

AB = $\frac{\mathrm{AC}.\mathrm{sinC}}{\mathrm{sinB}}$= $\frac{15.\sin 50°}{\sin 35°}$≈ 20,03cm

Vậy BC = 26,05cm và AB ≈ 20,03 cm.

2. Tính diện tích tam giác

Công thức tính diện tích tam giác:

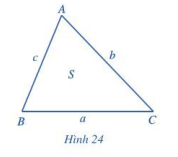
• Cho tam giác ABC có BC = a, CA = b, AB = c. Khi đó, diện tích S của tam giác ABC là:

S = $\frac{1}{2}$bc.sinA = $\frac{1}{2}$ca.sin = $\frac{1}{2}$ab.sinC

Ví dụ: Cho tam giác ABC có BC = $4\sqrt{2}$, $\widehat{\mathrm{A}}$= 45°, $\widehat{\mathrm{B}}$= 120°. Tính diện tích tam giác ABC.

Hướng dẫn giải:

Ta có:

$\widehat{\mathrm{A}}$ + $\widehat{\mathrm{B}}$ + $\widehat{\mathrm{C}}$= 180° (tổng ba góc trong tam giác)

Suy ra: $\widehat{\mathrm{C}}$= 180° – $\widehat{\mathrm{A}}$ – $\widehat{\mathrm{B}}$ = 180° – 45° – 120° = 15°

Áp dụng định lí sin trong tam giác ABC ta có:

$\frac{\mathrm{BC}}{\mathrm{sinA}}$ = $\frac{\mathrm{AC}}{\mathrm{sinB}}$ = $\frac{\mathrm{AB}}{\mathrm{sinC}}$

Suy ra:

AC = $\frac{\mathrm{BC}.\mathrm{sinB}}{\mathrm{sinA}}$ = $\frac{4\sqrt{2}.\sin 120°}{\sin 45°}$ = $4\sqrt{3}$;

AB = $\frac{\mathrm{AC}.\mathrm{sinC}}{\mathrm{sinB}}$= $\frac{4\sqrt{3}.\sin 15°}{\sin 120°}$ = $2\sqrt{6}-2\sqrt{2}$;

Diện tích tam giác ABC là:

S = $\frac{1}{2}$AC.AB.sinA = $\frac{1}{2}.4\sqrt{3}.(2\sqrt{6}-2\sqrt{2}).\sin 45°$ = $12-4\sqrt{3}$(đơn vị diện tích).

• Công thức Heron:

Công thức toán học Heron được sử dụng để tính diện tích của một tam giác theo độ dài ba cạnh như sau:

Cho tam giác ABC có BC = a, CA = b, AB = c, $\mathrm{p}=\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{2}$. Khi đó, diện tích S của tam giác ABC là:

$\mathrm{S}=\sqrt{\mathrm{p}(\mathrm{p}-\mathrm{a})(\mathrm{p}-\mathrm{b})(\mathrm{p}-\mathrm{c})}$.

Trong đó p là nửa chu vi tam giác ABC.

Ví dụ: Chứng minh công thức Heron.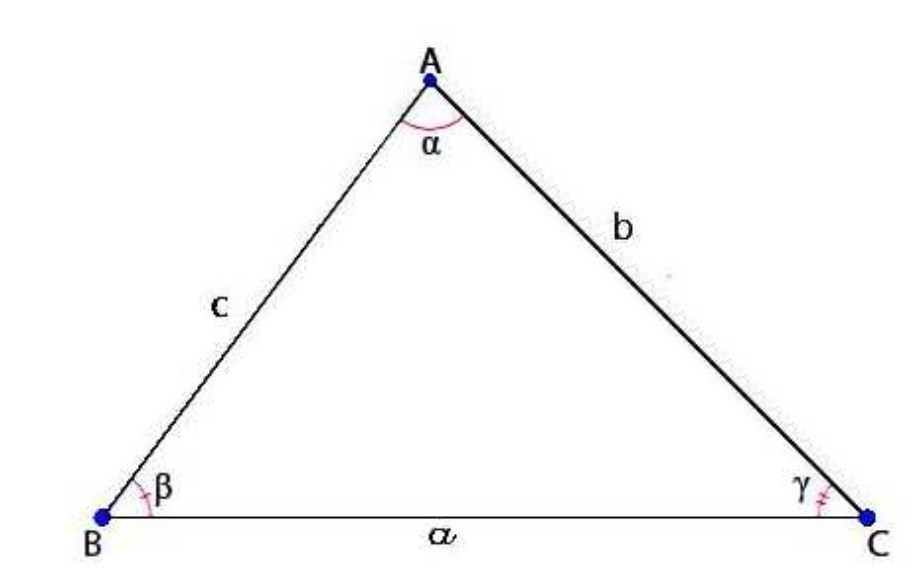

Hướng dẫn giải:

Gọi a, b, c lần lượt là 3 cạnh của tam giác và A, B, C lần lượt là các góc đối diện của các cạnh. Theo hệ quả định lý cosin, ta có:

cosC = $\frac{{\mathrm{a}}^2+{\mathrm{b}}^2-{\mathrm{c}}^2}{2\mathrm{ab}}$.

Mà:

sin²C + cos²C = 1

⇒ sinC = $\sqrt{1-{\cos }^2\mathrm{C}}$= $\sqrt{1-{\left(\frac{{\mathrm{a}}^2+{\mathrm{b}}^2-{\mathrm{c}}^2}{2\mathrm{ab}}\right)}^2}$= $\frac{\sqrt{4{\mathrm{a}}^2{\mathrm{b}}^2-{({\mathrm{a}}^2+{\mathrm{b}}^2-{\mathrm{c}}^2)}^2}}{2\mathrm{ab}}$

Ta có công thức tính diện tích tam giác ABC:

S = $\frac{1}{2}$absinC

= $\frac{1}{2}$ab. $\frac{\sqrt{4{\mathrm{a}}^2{\mathrm{b}}^2-{({\mathrm{a}}^2+{\mathrm{b}}^2-{\mathrm{c}}^2)}^2}}{2\mathrm{ab}}$

= $\frac{1}{4}$$\sqrt{4{\mathrm{a}}^2{\mathrm{b}}^2-{({\mathrm{a}}^2+{\mathrm{b}}^2-{\mathrm{c}}^2)}^2}$

= $\frac{1}{4}\sqrt{(2\mathrm{ab}-({\mathrm{a}}^2+{\mathrm{b}}^2-{\mathrm{c}}^2\left)\right)(2\mathrm{ab}+({\mathrm{a}}^2+{\mathrm{b}}^2-{\mathrm{c}}^2\left)\right)}$

= $\frac{1}{4}\sqrt{({\mathrm{c}}^2-{(\mathrm{a}-\mathrm{b})}^2)({(\mathrm{a}+\mathrm{b})}^2-{\mathrm{c}}^2)}$

= $\frac{1}{4}\sqrt{(\mathrm{c}-(\mathrm{a}-\mathrm{b}\left)\right)(\mathrm{c}+(\mathrm{a}-\mathrm{b}\left)\right)\left(\right(\mathrm{a}+\mathrm{b})-\mathrm{c})\left(\right(\mathrm{a}+\mathrm{b})+\mathrm{c})}$

= $\frac{1}{4}\sqrt{(\mathrm{a}+\mathrm{b}+\mathrm{c})(\mathrm{c}-\mathrm{a}+\mathrm{b})(\mathrm{c}+\mathrm{a}-\mathrm{b})(\mathrm{a}+\mathrm{b}-\mathrm{c})}$

= $\frac{1}{2}(\mathrm{a}+\mathrm{b}+\mathrm{c}).\frac{1}{2}(\mathrm{a}+\mathrm{b}+\mathrm{c}-2\mathrm{a}).\frac{1}{2}(\mathrm{a}+\mathrm{b}+\mathrm{c}-2\mathrm{b}).\frac{1}{2}(\mathrm{a}+\mathrm{b}+\mathrm{c}-2\mathrm{c})$

= $\sqrt{\mathrm{p}(\mathrm{p}-\mathrm{a})(\mathrm{p}-\mathrm{b})(\mathrm{p}-\mathrm{c})}$

Với $\mathrm{p}=\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{2}$.

Suy ra $\mathrm{S}=\sqrt{\mathrm{p}(\mathrm{p}-\mathrm{a})(\mathrm{p}-\mathrm{b})(\mathrm{p}-\mathrm{c})}$ (đpcm).

Ví dụ: Cho tam giác ABC có BC = 9, CA = 6, AB = 5. Tính diện tích tam giác ABC.

Hướng dẫn giải:

Nửa chu vi tam giác ABC là:

$\mathrm{p}=\frac{\mathrm{AB}+\mathrm{AC}+\mathrm{BC}}{2}$= $\frac{5+6+9}{2}$= 10

Áp dụng công thức Heron, diện tích tam giác ABC là:

$\mathrm{S}=\sqrt{\mathrm{p}(\mathrm{p}-\mathrm{AB})(\mathrm{p}-\mathrm{AC})(\mathrm{p}-\mathrm{BC})}$= $\sqrt{10(10-5)(10-6)(10-9)}$= $10\sqrt{2}$(đvdt)

3. Áp dụng vào bài toán thực tiễn

Trong thực tiễn, ta có thể áp dụng hệ thức lượng trong tam giác vào các bài toán như tính khoảng cách giữa hai vị trí, tính diện tích,... giúp cho việc tính toán trở nên chính xác và nhanh chóng hơn. Chúng ta có thể xem ví dụ sau:

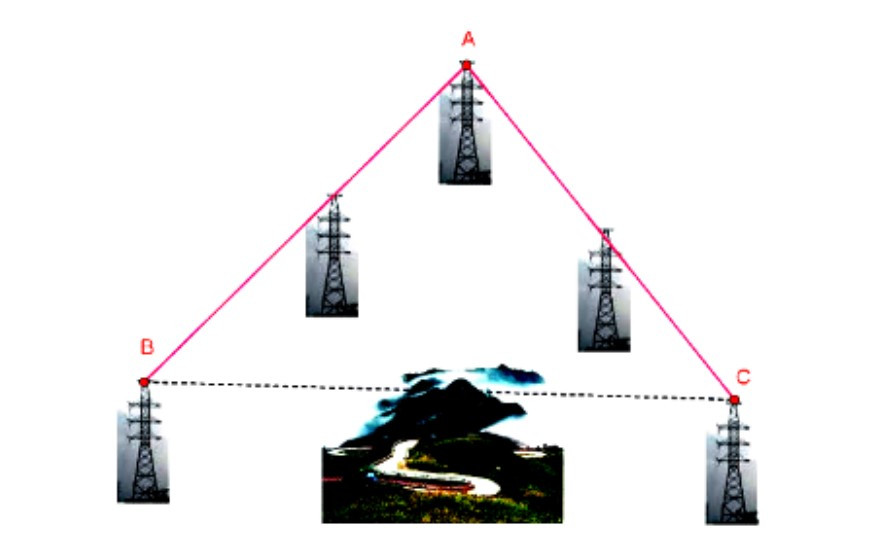
Ví dụ: Đường dây cao thế nối thẳng từ vị trí A đến vị trí B dài 10 km, từ vị trí A đến vị trí C dài 8 km, góc tạo bởi hai đường dây trên bằng 75°. Tính khoảng cách từ vị trí B đến vị trí C (làm tròn đến chữ số thập phân thứ 2).

Hướng dẫn giải:

Áp dụng định lí cosin vào tam giác ABC ta có:

BC² = AB² + AC² – 2AB.AC.cosA = 8² + 10² – 2.8.10.cos75° $\approx$ 122,59

BC $\approx$ 11,07

Vậy khoảng cách từ B đến C là khoảng 11,07 km.