Giải Toán 10 Bài 5 (Cánh diều): Tích của một số với một vectơ
Với giải bài tập Toán lớp 10 Bài 5: Tích của một số với một vectơ sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 Bài 5.
Giải bài tập Toán 10 Bài 5: Tích của một số với một vectơ
Mối liên hệ giữa hai vectơ vận tốc →v1, →v2 là như thế nào?
Lời giải:
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
Ta thấy hai vectơ →v1, →v2 là hai vectơ cùng phương nên →v1=k→v2 với k ≠ 0.
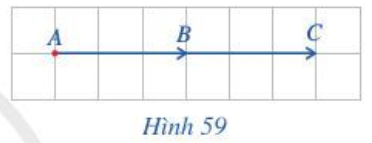
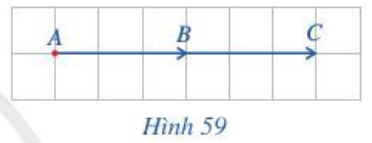
Hoạt động 1 trang 88 Toán lớp 10 Tập 1: Gọi B là trung điểm của AC.
Lời giải:
Do B là trung điểm của AC nên →BC=→AB.
Do đó →AB+→BC=→AB+→AB hay →AC=→AB+→AB.
Hoạt động 2 trang 88 Toán lớp 10 Tập 1: Gọi B là trung điểm của AC.
Quan sát vectơ →AB và →AC, nêu mối liên hệ về hướng và độ dài của vectơ 2→AB với →AB.
Lời giải:
Từ Hoạt động khám phá 1, ta có:
Mặt khác: nên .
Do đó vectơ cùng hướng với vectơ và .
Quan sát trên Hình 59, ta cũng thấy vectơ cùng hướng với vectơ và độ dài vectơ bằng 2 lần độ dài vectơ . Do đó vectơ cùng hướng với và .
Lời giải:
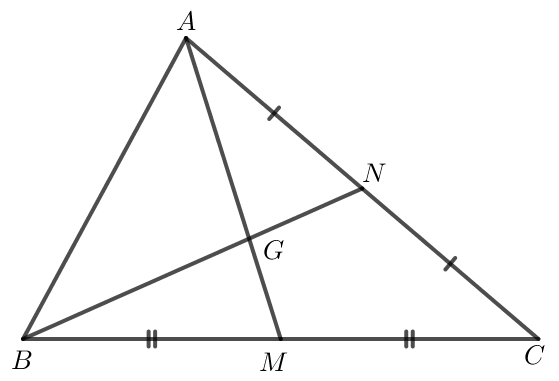
Tam giác ABC có hai đường trung tuyến AM và BN cắt nhau tại G nên G là trọng tâm của tam giác ABC.
Do đó AG = AM; GN = GB.
Vì AM là đường trung tuyến nên G thuộc đoạn AM
Do và là hai vectơ cùng hướng nên .
Vì BN là đường trung tuyến nên G thuộc đoạn BN.
Do và là hai vectơ cùng hướng nên .
Vậy a = ; b = .
Luyện tập 2 trang 89 Toán lớp 10 Tập 1: Cho ba điểm A, B, C. Chứng minh .
Lời giải:
Vậy .
Lời giải:
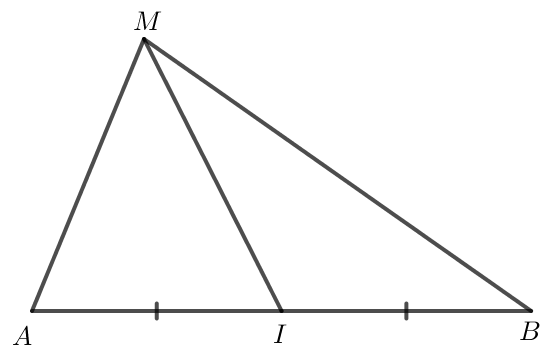
Ta có ; .
Do đó .
Do I là trung điểm của AB nên .
Do đó .
Vậy .
Lời giải:
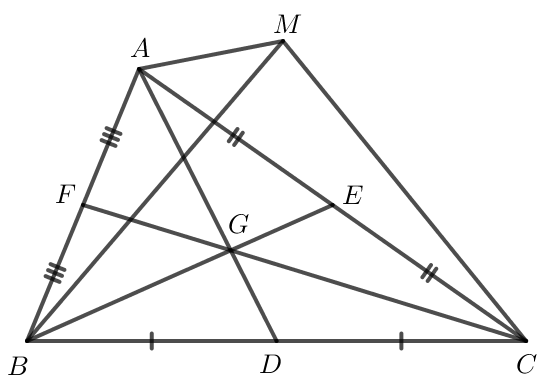
Gọi D, E, F lần lượt là trung điểm của BC, AC, AB.
Do D là trung điểm của BC nên .
Do E là trung điểm của AC nên .
Do F là trung điểm của AB nên .
Do đó .
.
Do G là trọng tâm của tam giác ABC nên
; ; .
Do đó .
Ta có
Vậy .
Luyện tập 3 trang 90 Toán lớp 10 Tập 1: Cho tam giác ABC có G là trọng tâm. Chứng minh .
Lời giải:
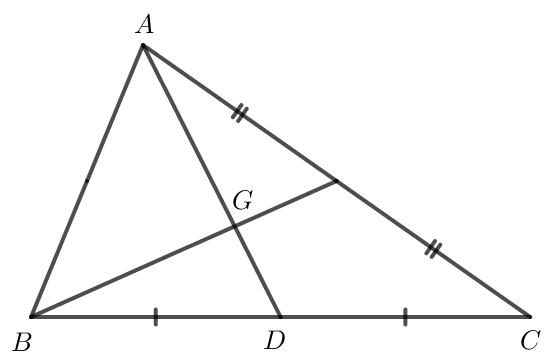
Gọi D là trung điểm của BC.
Do D là trung điểm của BC nên .
Do G là trọng tâm của tam giác ABC nên hay .
Do đó .
Vậy .
Lời giải:
Ta có với k là số thực khác 0. Khi đó hai vectơ và cùng phương.
Hoạt động 6 trang 91 Toán lớp 10 Tập 1: Cho ba điểm phân biệt A, B, C.
a) Nếu ba điểm A, B, C thẳng hàng thì hai vectơ có cùng phương hay không?
b) Ngược lại, nếu hai vectơ cùng phương thì ba điểm A, B, C có thẳng hàng hay không?
Lời giải:
a) Giá của vectơ là đường thẳng AB, giá của vectơ là đường thẳng AC.
Do A, B, C thẳng hàng nên đường thẳng AB trùng với đường thẳng AC.
Do đó hai vectơ cùng phương.
b) Giá của vectơ là đường thẳng AB, giá của vectơ là đường thẳng AC.
Hai vectơ cùng phương nên giá của chúng song song hoặc trùng nhau.
Mà AB và AC có điểm chung là A nên AB trùng AC.
Do đó A, B, C thẳng hàng.
Luyện tập 4 trang 91 Toán lớp 10 Tập 1: Ở Hình 61, tìm k trong mỗi trường hợp sau:
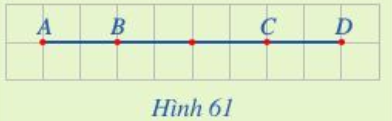
Lời giải:
a) Hai vectơ và là hai vectơ cùng hướng và AC = AD nên .
Vậy k = .
b) Hai vectơ và là hai vectơ ngược hướng và BD = 3DC nên .
Vậy k = -3.
Bài tập
Lời giải:
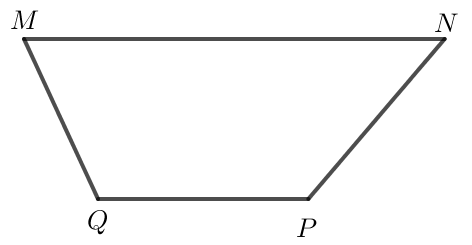
Ta thấy hai vectơ và là hai vectơ ngược hướng và MN = 2PQ nên .
Vậy đáp án đúng là đáp án C.
Bài 2 trang 92 Toán lớp 10 Tập 1: Cho đoạn thẳng AB = 6 cm.
Lời giải:
a) Ta thấy > 0 nên hai vectơ và cùng hướng.
Khi đó hay AC = AB và A, B, C thẳng hàng.
Do đó C là trung điểm của AB.
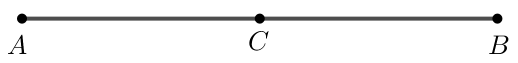
b) Ta thấy nên hai vectơ và ngược hướng.
Khi đó hay AD = AB và A, B, D thẳng hàng.
Do đó D nằm khác phía với B so với điểm A sao cho AD = AB.

Lời giải:
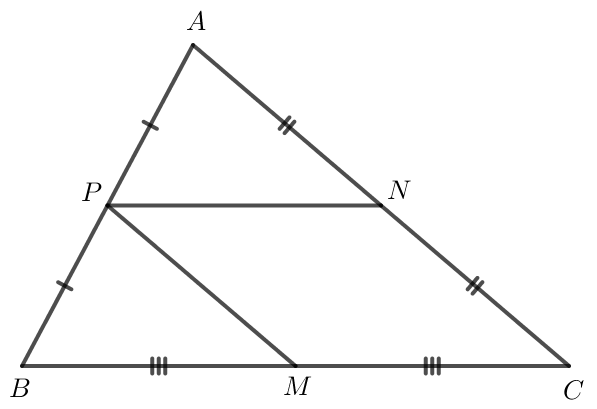
a) Tam giác ABC có P là trung điểm của AB; N là trung điểm của AC nên PN là đường trung bình của tam giác ABC.
Do đó PN // BC và PN = BC.
Ta thấy hai vectơ và cùng hướng và PN = BC nên .
Do đó .
Vậy .
b) Tam giác ABC có P là trung điểm của AB; M là trung điểm của BC nên PM là đường trung bình của tam giác ABC.
Do đó MP // CA và MP = CA.
Ta thấy hai vectơ và cùng hướng và MP = CA nên hay .
Do đó .
Vậy .
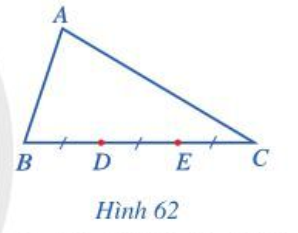
Lời giải:
Ta có ;
Do BD = DE = EC và BD + DE + EC = BC nên BD = DE = EC = BC.
Hai vectơ và cùng hướng và BD = BC nên .
Hai vectơ và cùng hướng và BE = 2BD nên .
Có nên .
Có nên .
c) Điểm G thuộc đoạn thẳng AE và .
Lời giải:
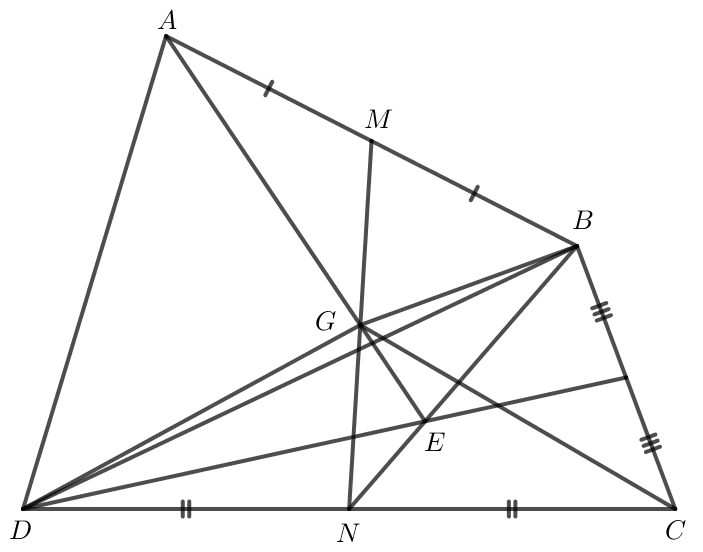
a) Do M là trung điểm của AB nên (1).
Do N là trung điểm của CD nên (2).
Do G là trung điểm của MN nên GM = GN.
Ta thấy hai vectơ và ngược hướng và GM = GN nên .
Do đó .
Từ (1) và (2) ta có .
Ta có
.
Vậy .
b) Do E là trọng tâm của tam giác BCD nên .
Do đó .
c) Do nên hai vectơ và cùng hướng.
Mà 4 > 0 nên G nằm giữa A và E.
Do đó hay EA = 4EG.
EG = EA
AG = EA.
Ta thấy hai vectơ và cùng hướng và AG = EA nên .
Lời giải:
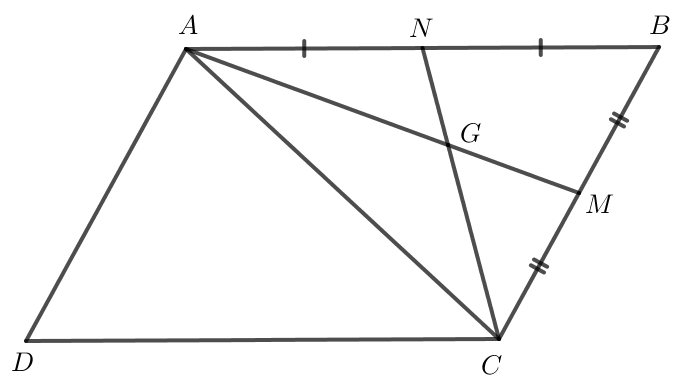
Gọi M và N lần lượt là trung điểm của BC và AB.
Do ABCD là hình bình hành nên .
Do M là trung điểm của BC nên BM = BC.
Hai vectơ và cùng hướng và BM = BC nên .
Do N là trung điểm của AB nên NB = AB.
Hai vectơ và ngược hướng và NB = AB nên .
Ta có ; .
Do G là trọng tâm của tam giác ABC nên và .
Do đó và .
Bài 7 trang 92 Toán lớp 10 Tập 1: Cho tam giác ABC. Các điểm D, E, H thỏa mãn
a) Biểu thị mỗi vectơ theo hai vectơ .
b) Chứng minh D, E, H thẳng hàng.
Lời giải:
Vì nên và cùng hướng và .
nên cùng hướng và AE = .
nên cùng hướng và .
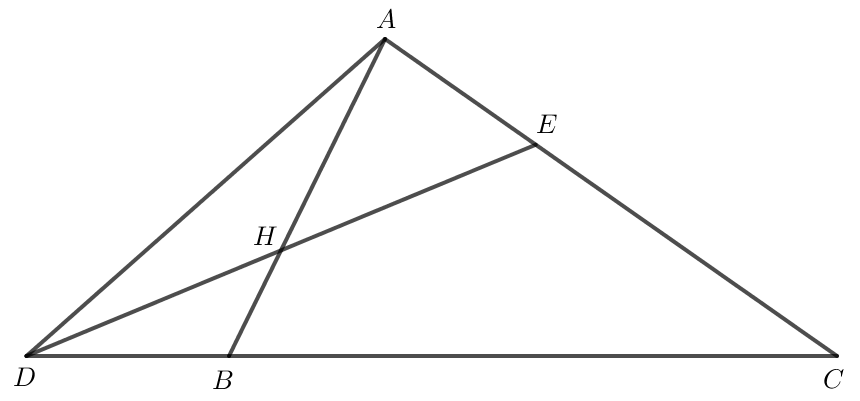
a) Do nên .
Ta có: .
.
.
b) Từ phần a ta thấy .
Do đó D, H, E thẳng hàng và H là trung điểm của DE.
Lý thuyết Toán 10 Bài 5. Tích của một số với một vectơ – Cánh diều
1. Định nghĩa
Cho một số k ≠ 0 và vectơ ≠ . Tích của một số k với vectơ là một vectơ, kí hiệu là k, được xác định như sau:
+ cùng hướng với nếu k > 0, ngược hướng với nếu k < 0;
+ có độ dài bằng .
Quy ước: 0 = , k =
Phép lấy tích của một số với một vectơ gọi là phép nhân một số với một vectơ.
Ví dụ: Cho G là trọng tâm của tam giác ABC, D và E lần lượt là trung điểm của BC và AC. Tìm mối quan hệ của và ; mối quan hệ của và
Hướng dẫn giải
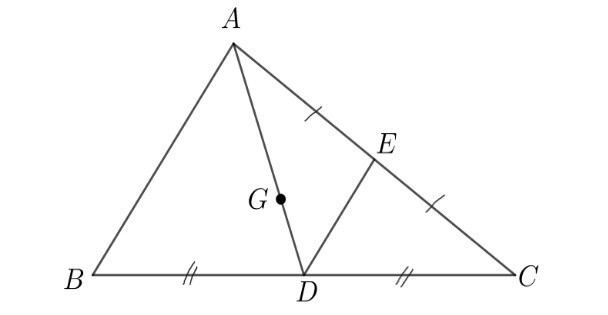
Khi đó ta có:
– Vì G là trọng tâm của tam giác ABC nên GA = 2GD.
Mà G nằm giữa A và D nên và là hai vectơ ngược hướng.
⇒ = (–2).
– Ta có: AD = 3GD.
Mà và là hai vectơ cùng hướng.
⇒ = 3.
Ví dụ: Cho vectơ có = 4. Tìm số thực x sao cho vectơ x có độ dài bằng 1 và cùng hướng với .
Hướng dẫn giải:
Ta có: = 1 ⇔ = 1 ⇔ = 1
⇔ =
Lại có vectơ x cùng hướng với vectơ nên x > 0
Suy ra x = .
Vậy x = là giá trị cần tìm.
2. Tính chất
Với hai vectơ bất kì , và hai số thực h, k, ta có:
+) k( + ) = k + k; k( – ) = k – k;
+) (h + k) = h + k;
+) h(k) = (hk);
+) 1 = ; (–1) = –.
Nhận xét: k = khi và chỉ khi k = 0 hoặc = .
Ví dụ: Tính:
a) 5 + 5;
b) 4 + 6;
c) 4(2) + 2 – 3.
Hướng dẫn giải:
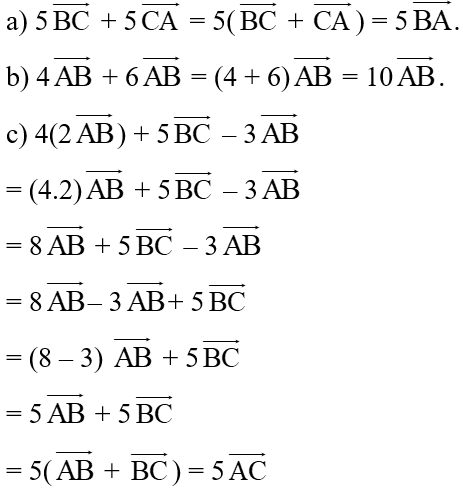
3. Một số ứng dụng
3.1. Trung điểm của đoạn thẳng
Nếu I là trung điểm của đoạn thẳng AB thì với điểm M bất kì.
Chứng minh:
Vì I là trung điểm của đoạn thẳng AB nên =
Suy ra:
=
= =
= = .
⇒ = (đpcm).
Ví dụ: Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của AC, BD. Chứng minh .
Hướng dẫn giải:
Vì M, N lần lượt là trung điểm của AC, BD nên ta có:
⇒ = = = .
⇒ (đpcm).
3.2. Trọng tâm của tam giác
Nếu G là trọng tâm của tam giác ABC thì với điểm M bất kì.
Ví dụ: Gọi G và G’ lần lượt là trọng tâm tam giác ABC và A’B’C’. Chứng minh rằng: .
Hướng dẫn giải:
Vì G và G’ lần lượt là trọng tâm tam giác ABC và A’B’C’ nên:
và
Theo quy tắc cộng vectơ ta có:
(1)
(2)
(3)
Cộng vế với vế của (1), (2) và (3) ta có:
=
=
=
= =
⇒ (đpcm).
3.3. Điều kiện để hai vectơ cùng phương. Điều kiện để ba điểm thẳng hàng
– Điều kiện cần và đủ để hai vectơ và ( ≠ 0) cùng phương là có một số thực k để = k.
– Điều kiện cần và đủ để ba điểm phân biệt A, B, C thẳng hàng là có số thực k để .
Nhận xét: Trong mặt phẳng, cho hai vectơ và không cùng phương. Với mỗi vectơ có duy nhất cặp số (x; y) thoả mãn .
Ví dụ: Cho tam giác ABC. Đặt , . Dựng các điểm M, N sao cho ; .
a) Phân tích , theo các vectơ và .
b) Gọi I là điểm thỏa mãn: . Chứng minh I, A, N thẳng hàng.
Hướng dẫn giải:
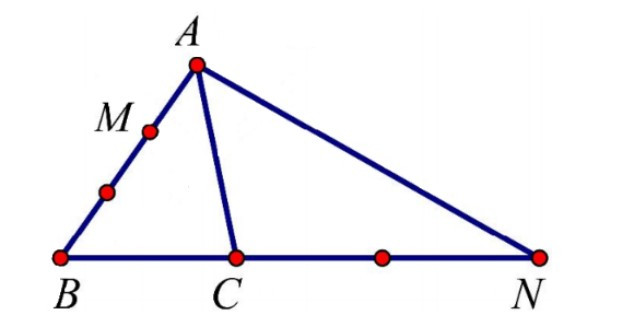
a) Ta có:
+) = = = – .
+) Vì ⇒ CN = 2BC ⇒ BC = BN ⇒ BN = 3BC.
⇒ .
⇒ = = = =
= = –2 + 3.
b) Ta có:
= = = + – = – =
⇒ = .
⇒ I, A, N thẳng hàng.
Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:
Bài 6: Tích vô hướng của hai vectơ
Bài 2: Tập hợp. Các phép toán trên tập hợp
Xem thêm tài liệu Toán lớp 10 Cánh diều hay, chi tiết khác:
Xem thêm các chương trình khác:
- Soạn văn lớp 10 (hay nhất) – Cánh Diều
- Tác giả tác phẩm Ngữ văn lớp 10 – Cánh Diều
- Tóm tắt tác phẩm Ngữ văn lớp 10 – Cánh Diều
- Bố cục tác phẩm Ngữ văn lớp 10 – Cánh Diều
- Nội dung chính tác phẩm Ngữ văn lớp 10 – Cánh Diều
- Soạn văn lớp 10 (ngắn nhất) – Cánh Diều
- Giải sbt Ngữ văn lớp 10 – Cánh Diều
- Văn mẫu lớp 10 – Cánh Diều
- Giải Chuyên đề học tập Ngữ văn 10 – Cánh diều
- Giải sgk Tiếng Anh 10 – Explore new worlds
- Giải sgk Tiếng Anh 10 – ilearn Smart World
- Trọn bộ Từ vựng Tiếng Anh 10 ilearn Smart World đầy đủ nhất
- Ngữ pháp Tiếng Anh 10 i-learn Smart World
- Giải sbt Tiếng Anh 10 - iLearn Smart World
- Giải sgk Vật lí 10 – Cánh Diều
- Giải sbt Vật lí 10 – Cánh Diều
- Lý thuyết Vật lí 10 – Cánh Diều
- Giải Chuyên đề Vật lí 10 – Cánh Diều
- Giải sgk Hóa học 10 – Cánh Diều
- Lý thuyết Hóa học 10 – Cánh Diều
- Giải sbt Hóa học 10 – Cánh Diều
- Giải Chuyên đề Hóa học 10 – Cánh Diều
- Giải sgk Sinh học 10 – Cánh Diều
- Giải sbt Sinh học 10 – Cánh Diều
- Lý thuyết Sinh học 10 – Cánh Diều
- Giải Chuyên đề Sinh học 10 – Cánh diều
- Giải sgk Lịch sử 10 – Cánh Diều
- Giải sbt Lịch sử 10 – Cánh Diều
- Giải Chuyên đề Lịch sử 10 – Cánh Diều
- Lý thuyết Lịch sử 10 – Cánh diều
- Giải sgk Địa lí 10 – Cánh Diều
- Lý thuyết Địa Lí 10 – Cánh Diều
- Giải sbt Địa lí 10 – Cánh Diều
- Giải Chuyên đề Địa lí 10 – Cánh Diều
- Lý thuyết Công nghệ 10 – Cánh Diều
- Giải sgk Công nghệ 10 – Cánh Diều
- Giải sgk Giáo dục Kinh tế và Pháp luật 10 – Cánh Diều
- Giải sbt Giáo dục Kinh tế và Pháp luật 10 – Cánh Diều
- Giải Chuyên đề Kinh tế pháp luật 10 – Cánh diều
- Lý thuyết KTPL 10 – Cánh diều
- Lý thuyết Giáo dục quốc phòng 10 – Cánh Diều
- Giải sgk Giáo dục quốc phòng - an ninh 10 – Cánh diều
- Giải sbt Giáo dục quốc phòng - an ninh 10 – Cánh Diều
- Giải sgk Hoạt động trải nghiệm 10 – Cánh Diều
- Giải sbt Hoạt động trải nghiệm 10 – Cánh Diều
- Giải sgk Tin học 10 – Cánh Diều
- Giải sbt Tin học 10 – Cánh Diều
- Giải Chuyên đề Tin học 10 – Cánh diều
- Lý thuyết Tin học 10 - Cánh diều
- Giải sgk Giáo dục thể chất 10 – Cánh Diều