Giải Toán 10 Bài 6 (Cánh diều): Tích vô hướng của hai vectơ
Với giải bài tập Toán lớp 10 Bài 6: Tích vô hướng của hai vectơ sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 Bài 6.
Giải bài tập Toán 10 Bài 6: Tích vô hướng của hai vectơ
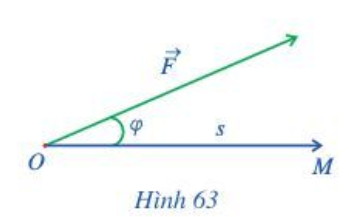
Trong toán học, giá trị của biểu thức (không kể đơn vị đo) được gọi là gì?
Lời giải:
Giá trị của biểu thức là tích vô hướng của hai vectơ và .
Luyện tập 1 trang 93 Toán lớp 10 Tập 1: Cho tam giác ABC vuông tại A có , AB = 3 cm. Tính .
Lời giải:
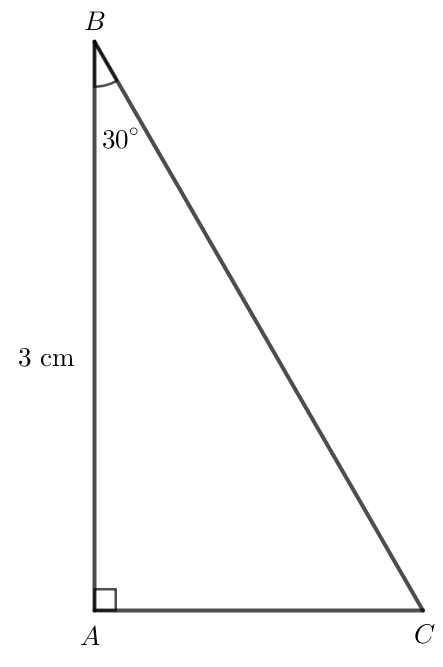
Tam giác ABC vuông tại A nên .
cm.
cm.
Ta có: (trong tam giác vuông, hai góc nhọn phụ nhau).
.
Khi đó
=
= = 6 . cos 60° = 3.
Luyện tập 2 trang 95 Toán lớp 10 Tập 1: Cho tam giác ABC đều cạnh a, AH là đường cao. Tính:
Lời giải:
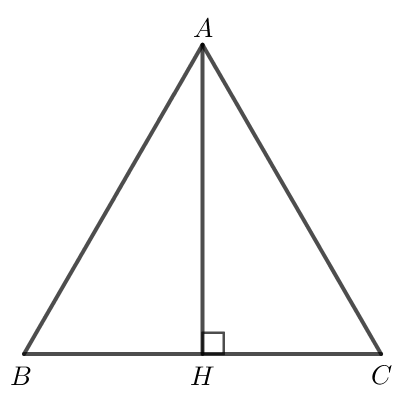
a) Do tam giác ABC đều nên và AB = BC = CA = a.
Khi đó
= -a.a.cos 60o = .
Vậy
b) Do AH là đường cao của tam giác ABC nên .
Do đó nên .
Luyện tập 3 trang 96 Toán lớp 10 Tập 1: Chứng minh rằng với hai vectơ bất kì , ta có:
Lời giải:
Ta có:
+) Ta có:
+) Ta có:
Lời giải:
Phần thuận: Tam giác ABC vuông tại A thì BC2 = AB2 + AC2.
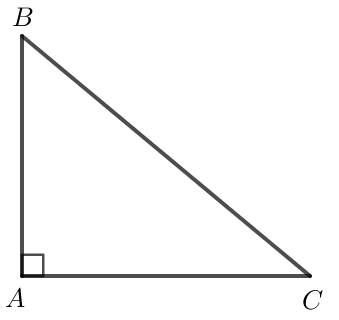
Xét tam giác ABC vuông tại A, ta có:
Áp dụng định lí côsin trong tam giác ABC:
BC2 = AB2 + AC2 - 2.AB.AC.cos
BC2 = AB2 + AC2 - 2.AB.AC.cos 90o
BC2 = AB2 + AC2 - 2.AB.AC.0
BC2 = AB2 + AC2
Phần đảo: Tam giác ABC có BC2 = AB2 + AC2 thì tam giác ABC vuông tại A.
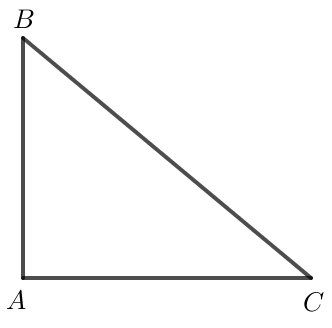
Áp dụng định lí côsin trong tam giác ABC:
BC2 = AB2 + AC2 - 2.AB.AC.cos
Mà BC2 = AB2 + AC2 nên -2.AB.AC.cos = 0.
Do AB và AC là độ dài các cạnh của tam giác nên cos = 0.
Do đó .
Vậy tam giác ABC vuông tại A.
Bài tập
Lời giải:
Ta có .
Do đó -MN2 = -4 nên MN2 = 4.
Mà MN > 0 (độ dài đoạn thẳng) nên MN = 2.
Vậy đáp án đúng là đáp án B.
Bài 2 trang 98 Toán lớp 10 Tập 1: Phát biểu nào sau đây là đúng?
Lời giải:
Nếu khác và thì .
Do đó .
Vậy đáp án đúng là đáp án C.
Bài 3 trang 98 Toán lớp 10 Tập 1: Tính trong mỗi trường hợp sau:
Lời giải:
a)
= 3 . 4 . cos 30o = .
b)
= 5 . 6 . cos 120o = -15.
c) Do và cùng hướng nên = 2 . 3 = 6.
d) Do và ngược hướng nên = -2 . 3 = -6.
Bài 4 trang 98 Toán lớp 10 Tập 1: Cho hình vuông ABCD cạnh a. Tính các tích vô hướng sau:
Lời giải:
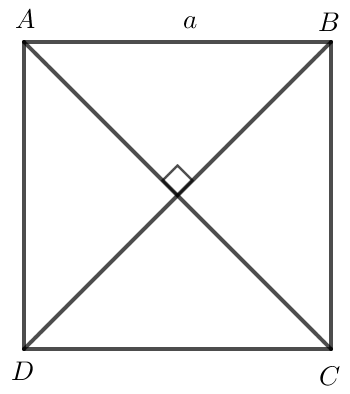
a) Do ABCD là hình vuông nên .
Áp dụng định lí Pythagore vào tam giác ABC vuông tại B:
AC2 = AB2 + BC2 = a2 + a2 = 2a2.
AC = a.
Khi đó:
= a . a . cos = a . a . cos 45o = a2.
b) ABCD là hình vuông nên hai đường chéo AC và BD vuông góc với nhau.
Do đó nên .
Bài 5 trang 98 Toán lớp 10 Tập 1: Cho tam giác ABC. Chứng minh:
Lời giải:
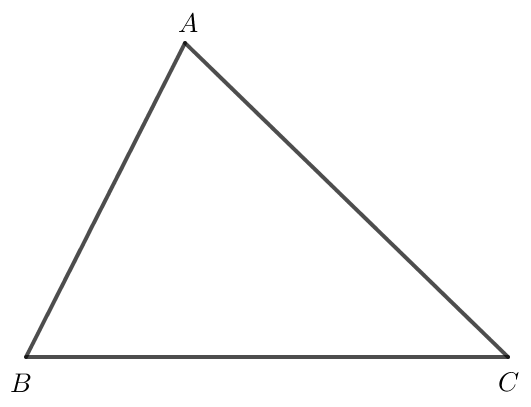
= 0.
Vậy .
Bài 6 trang 98 Toán lớp 10 Tập 1: Cho tam giác nhọn ABC, kẻ đường cao AH. Chứng minh rằng:
Lời giải:
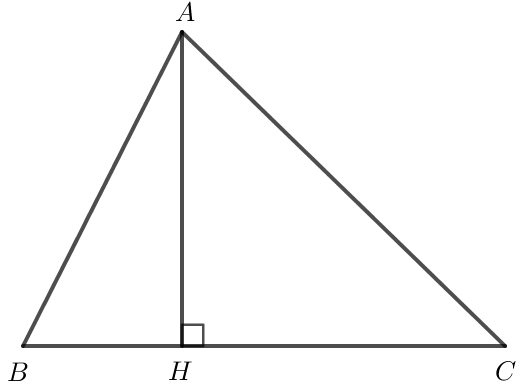
a) Do AH là đường cao của tam giác ABC nên AH BC.
Do đó nên .
Ta có
Vậy .
b) Ta có
Vậy .
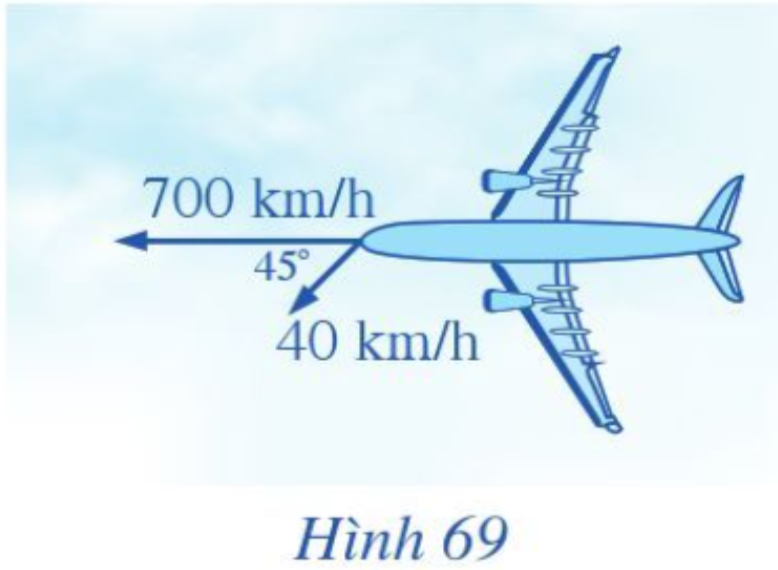
Lời giải:
Gọi vận tốc của máy bay theo hướng từ đông sang tây là , vận tốc gió thổi từ hướng đông bắc sang tây nam là , khi đó vận tốc mới của máy bay là .
Ta có = 700, = 40.
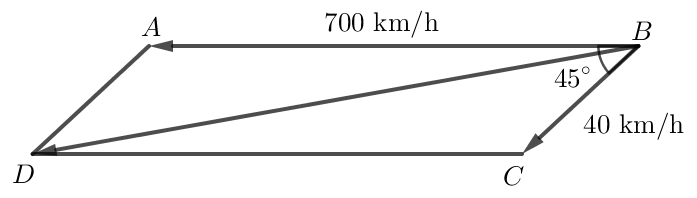
Do ABCD là hình bình hành nên AB = CD = 700 và .
Do đó .
Áp dụng định lí côsin vào tam giác BCD:
BD2 = BC2 + CD2 - 2.BC.CD.cos .
BD2 = 402 + 7002 - 2.40.700.cos 135o.
BD2 ≈ 531 197,98.
BD ≈ 728,83 km.
Vậy vận tốc mới của máy bay sau khi gặp gió thổi khoảng 728,83 km/h.
Lời giải:
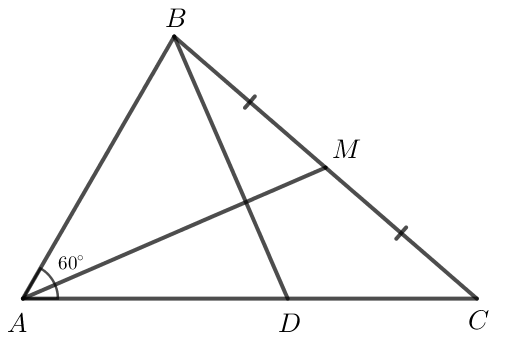
a) Ta có
= 2 . 3 . cos 60o = 3.
Vậy = 3.
b) Do M là trung điểm của BC nên .
Ta có .
c) Ta có
= 0.
Do đó AM ⊥ BD.
Lý thuyết Toán 10 Bài 6. Tích vô hướng của hai vectơ – Cánh diều
1. Định nghĩa
1.1. Tích vô hướng của hai vectơ có cùng điểm đầu
– Góc giữa hai vectơ , là góc giữa hai tia OA, OB và được kí hiệu là
– Tích vô hướng của hai vectơ và là một số thực, kí hiệu là ., được xác định bởi công thức: .
Ví dụ: Cho tam giác ABC đều cạnh 2a có đường cao AH. Tính tích vô hướng của .
Hướng dẫn giải:
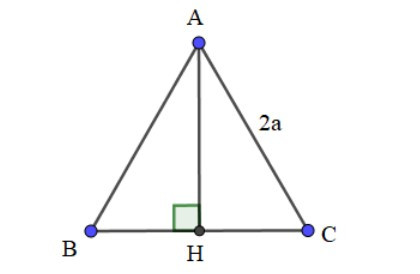
Vì tam giác ABC đều nên = 60°
⇒ = = 60°
Ta có:
=
⇒ = AB.AC.cos = AB.AC.cos60° = 2a.2a. = 2a2.
1.2. Tích vô hướng của hai vectơ tùy ý
Định nghĩa:
Cho hai vectơ , khác Lấy một điểm O và vẽ vectơ (Hình vẽ).
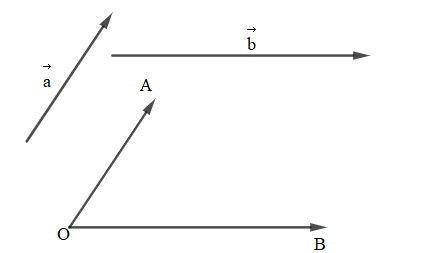
+ Góc giữa hai vectơ , , kí hiệu , là góc giữa hai vectơ , .
+ Tích vô hướng của hai vectơ và , kí hiệu . là tích vô hướng của hai vectơ và . Như vậy, tích vô hướng của hai vectơ và là một số thực được xác định bởi công thức: . = .
Quy ước: Tích vô hướng của một vectơ bất kì với vectơ là số 0.
Chú ý:
+) =
+) Nếu = 90° thì ta nói hai vectơ , vuông góc với nhau, kí hiệu ⊥ hoặc ⊥ . Khi đó . = = 0.
+) Tích vô hướng của hai vectơ cùng hướng bằng tích hai độ dài của chúng.
+) Tích vô hướng của hai vectơ ngược hướng bằng số đối của tích hai độ dài của chúng.
Ví dụ: Cho tam giác vuông cân ABC có AB = AC = a. Tính các tích vô hướng ,.
Hướng dẫn giải:
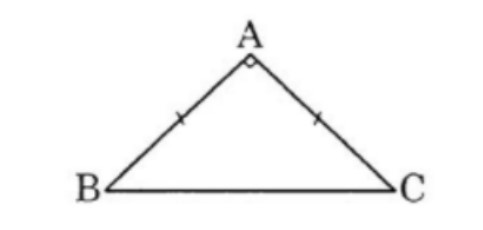
+ Vì tam giác ABC vuông cân, mà AB = AC
⇒ Tam giác ABC vuông cân tại A.
⇒ AB ⊥ AC
⇒ = = = 0
+ Ta có: BC = = = a.
⇒ = = a. a.cos135° = a. a. = –a2.
2. Tính chất
Với hai vectơ bất kì , và số thực k tùy ý, ta có:
+) . = . (tính chất giao hoán);
+) (tính chất phân phối);
+) ;
+) ≥ 0, = 0 ⟺ = .
Trong đó, kí hiệu . = và biểu thức này được gọi là bình phương vô hướng của vectơ .
Ví dụ: Cho 4 điểm A, B, C, D bất kì. Chứng minh: .
Hướng dẫn giải:
Ta có:
= = (tính chất phân phối)
= = = (tính chất phân phối)
= = = (tính chất phân phối)
= (tính chất giao hoán và kết hợp)
= 0
⟺ (đpcm).
3. Một số ứng dụng
3.1. Tính độ dài của đoạn thẳng
Nhận xét:
Với hai điểm A, B phân biệt, ta có: .
Do đó độ dài đoạn thẳng AB được tính như sau: AB =
3.2. Chứng minh hai đường thẳng vuông góc
Nhận xét:
+ Cho hai vectơ bất kì và khác vectơ . Ta có: . = 0 ⟺ ⊥ .
Hai đường thẳng AB và CD vuông góc với nhau khi và chỉ khi + Hai đường thẳng a và b vuông góc khi và chỉ khi , trong đó ≠ 0, ≠ 0, giá của vectơ song song hoặc trùng với đường thẳng a và giá của vectơ song song hoặc trùng với đường thẳng b.
Ví dụ: Cho hai vectơ và vuông góc với nhau và , . Chứng minh hai vectơ 2 – và + vuông góc với nhau.
Hướng dẫn giải:
Vì và vuông góc với nhau ⟺ . = 0
Ta có:
= = =
= 2.12 + 0 – = 0
Vì tích của hai vectơ 2 – và + bằng 0 nên chúng vuông góc với nhau.
Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:
Bài 2: Tập hợp. Các phép toán trên tập hợp
Xem thêm tài liệu Toán lớp 10 Cánh diều hay, chi tiết khác:
Xem thêm các chương trình khác:
- Soạn văn lớp 10 (hay nhất) – Cánh Diều
- Tác giả tác phẩm Ngữ văn lớp 10 – Cánh Diều
- Tóm tắt tác phẩm Ngữ văn lớp 10 – Cánh Diều
- Bố cục tác phẩm Ngữ văn lớp 10 – Cánh Diều
- Nội dung chính tác phẩm Ngữ văn lớp 10 – Cánh Diều
- Soạn văn lớp 10 (ngắn nhất) – Cánh Diều
- Giải sbt Ngữ văn lớp 10 – Cánh Diều
- Văn mẫu lớp 10 – Cánh Diều
- Giải Chuyên đề học tập Ngữ văn 10 – Cánh diều
- Giải sgk Tiếng Anh 10 – Explore new worlds
- Giải sgk Tiếng Anh 10 – ilearn Smart World
- Trọn bộ Từ vựng Tiếng Anh 10 ilearn Smart World đầy đủ nhất
- Ngữ pháp Tiếng Anh 10 i-learn Smart World
- Giải sbt Tiếng Anh 10 - iLearn Smart World
- Giải sgk Vật lí 10 – Cánh Diều
- Giải sbt Vật lí 10 – Cánh Diều
- Lý thuyết Vật lí 10 – Cánh Diều
- Giải Chuyên đề Vật lí 10 – Cánh Diều
- Giải sgk Hóa học 10 – Cánh Diều
- Lý thuyết Hóa học 10 – Cánh Diều
- Giải sbt Hóa học 10 – Cánh Diều
- Giải Chuyên đề Hóa học 10 – Cánh Diều
- Giải sgk Sinh học 10 – Cánh Diều
- Giải sbt Sinh học 10 – Cánh Diều
- Lý thuyết Sinh học 10 – Cánh Diều
- Giải Chuyên đề Sinh học 10 – Cánh diều
- Giải sgk Lịch sử 10 – Cánh Diều
- Giải sbt Lịch sử 10 – Cánh Diều
- Giải Chuyên đề Lịch sử 10 – Cánh Diều
- Lý thuyết Lịch sử 10 – Cánh diều
- Giải sgk Địa lí 10 – Cánh Diều
- Lý thuyết Địa Lí 10 – Cánh Diều
- Giải sbt Địa lí 10 – Cánh Diều
- Giải Chuyên đề Địa lí 10 – Cánh Diều
- Lý thuyết Công nghệ 10 – Cánh Diều
- Giải sgk Công nghệ 10 – Cánh Diều
- Giải sgk Giáo dục Kinh tế và Pháp luật 10 – Cánh Diều
- Giải sbt Giáo dục Kinh tế và Pháp luật 10 – Cánh Diều
- Giải Chuyên đề Kinh tế pháp luật 10 – Cánh diều
- Lý thuyết KTPL 10 – Cánh diều
- Lý thuyết Giáo dục quốc phòng 10 – Cánh Diều
- Giải sgk Giáo dục quốc phòng - an ninh 10 – Cánh diều
- Giải sbt Giáo dục quốc phòng - an ninh 10 – Cánh Diều
- Giải sgk Hoạt động trải nghiệm 10 – Cánh Diều
- Giải sbt Hoạt động trải nghiệm 10 – Cánh Diều
- Giải sgk Tin học 10 – Cánh Diều
- Giải sbt Tin học 10 – Cánh Diều
- Giải Chuyên đề Tin học 10 – Cánh diều
- Lý thuyết Tin học 10 - Cánh diều
- Giải sgk Giáo dục thể chất 10 – Cánh Diều