Giải Toán 10 Bài 1 (Cánh diều): Mệnh đề toán học

Giải bài tập Toán 10 Bài 1: Mệnh đề toán học

Video giải bài tập Toán 10 Bài 1: Mệnh đề toán học

Câu hỏi khởi động

Giải Toán 10 trang 5 Tập 1

Câu hỏi khởi động trang 5 Toán lớp 10 Tập 1: Bạn H’Maryam phát biểu: “Số 15 chia hết cho 5.”, bạn Phương phát biểu: “Việt Nam là một nước ở khu vực Đông Nam Á.”. Trong hai phát biểu trên, phát biểu nào là mệnh đề toán học?

Lời giải:

Sau bài học trên ta biết được:

Mệnh đề toán học là khẳng định về một sự kiện trong toán học.

Ta thấy phát biểu của bạn H’Maryam là một khẳng định về sự kiện toán học. Do đó phát biểu này là mệnh đề toán học.

Còn phát biểu của bạn Phương là một khẳng định không về sự kiện toán học. Do đó không phải là mệnh đề toán học.

1. Mệnh đề toán học

Hoạt động 1 trang 5 Toán lớp 10 Tập 1:

a) Phát biểu của bạn H’Maryam có phải là một câu khẳng định về tính chất chia hết trong toán học hay không?

b) Phát biểu của bạn Phương có phải là một câu khẳng định về một sự kiện trong toán học hay không?

Lời giải:

a) Phát biểu “số 15 chia hết cho 5” của bạn H’Maryam là một mệnh đề khẳng định về một sự kiện trong toán học nói về tính chất chia hết. Ta gọi đây là mệnh đề toán học.

b) Phát biểu “Việt Nam là một nước ở khu vực Đông Nam Á” của bạn Phương không phải là một câu khẳng định về một sự kiện trong toán học. Do đó phát biểu này không phải là mệnh đề toán học.

Luyện tập 1 trang 5 Toán lớp 10 Tập 1: Nêu hai ví dụ về mệnh đề toán học.

Lời giải:

Một số ví dụ về mệnh đề toán học là:

- Số 15 là hợp số.

- Đường trung trực của đoạn thẳng AB là đường thẳng đi qua trung điểm của đoạn thẳng AB.

…

Ngoài ra còn rất nhiều ví dụ khác nữa.

Giải Toán 10 trang 6 Tập 1

Hoạt động 2 trang 6 Toán lớp 10 Tập 1: Trong các mệnh đề toán học sau đây, mệnh đề nào là một khẳng định đúng? Mệnh đề nào là một khẳng định sai?

P: “Tổng hai góc đối của một tứ giác nội tiếp bằng 180°”;

Q: “ $\sqrt{2}$ là số hữu tỉ”.

Lời giải:

Nhắc lại kiến thức Toán 9:

Trong tứ giác nội tiếp, tổng hai góc đối bằng 180⁰

Do đó mệnh đề P là một khẳng định đúng.

Ta có $\sqrt{2}$ là số vô tỉ mà số vô tỉ không phải số hữu tỉ nên mệnh đề Q là một khẳng định sai.

Vậy P là mệnh đề đúng, Q là mệnh đề sai.

Luyện tập 2 trang 6 Toán lớp 10 Tập 1: Nêu ví dụ về một mệnh đề đúng và một mệnh đề sai.

Lời giải:

+ Ví dụ về mệnh đề đúng:

H: “Hình bình hành là hình có các cặp cạnh đối bằng nhau”

+ Ví dụ về mệnh đề sai:

K: “109 là một số chẵn” (109 là một số lẻ chứ không phải một số chẵn do đó mệnh đề K là sai).

2. Mệnh đề chứa biến

Hoạt động 3 trang 6 Toán lớp 10 Tập 1: Xét câu “n chia hết cho 3” với n là số tự nhiên.

a) Ta có thể khẳng định được tính đúng sai của câu trên hay không?

b) Với n = 21 thì câu “21 chia hết cho 3” có phải là mệnh đề toán học hay không? Nếu là mệnh đề toán học thì mệnh đề đó đúng hay sai?

c) Với n = 10 thì câu “10 chia hết cho 3” có phải là mệnh đề toán học hay không? Nếu là mệnh đề toán học thì mệnh đề đó đúng hay sai?

Lời giải:

a) Với mỗi giá trị của n thì câu đã cho có tính đúng, sai khác nhau. Do đó ta chưa thể khẳng định được tính đúng sai của câu “n chia hết cho 3”.

b) Với n = 21 thì câu “21 chia hết cho 3” là mệnh đề toán học vì nó khẳng định một sự kiện trong toán học đó là quan hệ chia hết.

Vì 21 = 3.7 nên 21 chia hết cho 3.

Suy ra câu “21 chia hết cho 3” là mệnh đề đúng.

c) Với n = 10 thì câu “10 chia hết cho 3” cũng là một mệnh đề toán học vì nó khẳng định một sự kiện trong toán học đó là quan hệ chia hết.

Vì 10 không chia hết cho 3 nên câu “10 chia hết cho 3” là mệnh đề sai.

Luyện tập 3 trang 6 Toán lớp 10 Tập 1: Nêu ví dụ về mệnh đề chứa biến.

Lời giải:

Một số ví dụ về mệnh đề chứa biến:

+) A(x): “7x² – 10 = 0”;

+) B(t): “t là một số nguyên tố”.

3. Phủ định của một mệnh đề

Giải Toán 10 trang 7 Tập 1

Hoạt động 4 trang 7 Toán lớp 10 Tập 1: Hai bạn Kiên và Cường đang tranh luận với nhau.

Kiên nói: “Số 23 là số nguyên tố”.

Cường nói: “Số 23 không là số nguyên tố”.

Em có nhận xét gì về hai câu phát biểu của Kiên và Cường?

Lời giải:

Hai câu phát biểu của Kiên và Cường đều nói về một sự kiện toán học nên cả hai phát biểu là các mệnh đề toán học.

Phát biểu của Cường là phát biểu phủ định lại phát biểu của Kiên.

Số 23 là số tự nhiên lớn hơn 1 và chỉ có hai ước là 1 và chính nó. Suy ra 23 là số nguyên tố. Do đó phát biểu của Kiên là mệnh đề đúng, còn phát biểu của Cường là mệnh đề sai.

Luyện tập 4 trang 7 Toán lớp 10 Tập 1: Lập mệnh đề phủ định của mỗi mệnh đề sau và nhận xét tính đúng sai của mệnh đề phủ định đó.

P: “5,15 là một số hữu tỉ”;

Q: “ 2 023 là số chẵn”.

Lời giải:

+ P: “5,15 là một số hữu tỉ”

Mệnh đề phủ định của P là $\overline{P}$: “5,15 không phải là một số hữu tỉ”

Ta có: $5,15=\frac{515}{100}$ trong đó $515;100\in \mathbb{Z},100\ne 0$ nên 5,15 là một số hữu tỉ. Do đó mệnh đề P đúng còn mệnh đề $\overline{P}$ sai.

+ Q: “2 023 là số chẵn”

Mệnh đề phủ định của Q là $\overline{Q}$: “2 023 không phải là số chẵn” hay $\overline{Q}$: “2 023 là số lẻ”.

Số 2 023 có chữ số tận cùng là 3 nên 2 023 là số lẻ. Do đó mệnh đề Q sai còn mệnh đề $\overline{Q}$ là mệnh đề đúng.

4. Mệnh đề kéo theo

Hoạt động 5 trang 7 Toán lớp 10 Tập 1: Xét hai mệnh đề:

P: “Số tự nhiên n chia hết cho 6”; Q: “Số tự nhiên n chia hết cho 3”.

Xét mệnh đề R: “Nếu số tự nhiên n chia hết cho 6 thì số tự nhiên n chia hết cho 3”.

Mệnh đề R có dạng phát biểu như thế nào?

Lời giải:

Xét mệnh đề R: “Nếu số tự nhiên n chia hết cho 6 thì số tự nhiên n chia hết cho 3”.

Vế nếu “số tự nhiên n chia hết cho 6” chính là mệnh đề P.

Vế thì “số tự nhiên n chia hết cho 3” chính là mệnh đề Q.

Do đó mệnh đề R có dạng: “Nếu P thì Q”.

Giải Toán 10 trang 8 Tập 1

Luyện tập 5 trang 8 Toán lớp 10 Tập 1: Hãy phát biểu một định lí toán học ở dạng mệnh đề kéo theo P ⇒ Q.

Lời giải:

Một ví dụ về định lí toán học ở dạng mệnh đề kéo theo P ⇒ Q: Định lí Pi – ta – go đảo:

Nếu tam giác có bình phương một cạnh bằng tổng các bình phương của hai cạnh còn lại thì tam giác đó là tam giác vuông.

Trong đó: P: “tam giác có bình phương một cạnh bằng tổng các bình phương của hai cạnh còn lại “

Q: “tam giác đó là tam giác vuông”.

5. Mệnh đề đảo. Hai mệnh đề tương đương

Hoạt động 6 trang 8 Toán lớp 10 Tập 1: Cho tam giác ABC. Xét mệnh đề dạng P ⇒ Q như sau:

“Nếu tam giác ABC vuông tại A thì tam giác ABC có AB² + AC² = BC²”.

Phát biểu mệnh đề Q ⇒ P và xác định tính đúng sai của hai mệnh đề P ⇒ Q và Q ⇒ P.

Lời giải:

Trong mệnh đề P ⇒ Q, ta có: P: “Tam giác ABC vuông tại A” và Q: “Tam giác ABC có AB² + AC² = BC²”.

Suy ra mệnh đề Q ⇒ P: “Nếu tam giác ABC có AB² + AC² = BC² thì tam giác ABC vuông tại A”.

Theo định lí Py – ta – go thì mệnh đề P ⇒ Q là mệnh đề đúng.

Theo định lí Py – ta – go đảo thì mệnh đề Q ⇒ P là mệnh đề đúng.

Luyện tập 6 trang 8 Toán lớp 10 Tập 1: Cho tam giác ABC. Từ các mệnh đề:

P: “Tam giác ABC đều”, Q: “Tam giác ABC cân và có một góc bằng 60°”, hãy phát biểu hai mệnh đề P ⇒ Q và Q ⇒ P và xác định tính đúng sai của mỗi mệnh đề đó. Nếu cả hai mệnh đề trên đều đúng, hãy phát biểu mệnh đề tương đương.

Lời giải:

+ Mệnh đề P ⇒ Q: “Nếu tam giác ABC đều thì tam giác ABC cân và có một góc bằng 60°”.

Nếu tam giác ABC đều thì AB = AC = BC và $\widehat{A}=\widehat{B}=\widehat{C}={60}^0$

⇒ AB = AC

⇒ tam giác ABC cân và có một góc bằng 60⁰.

Do đó mệnh đề P ⇒ Q đúng.

+ Mệnh đề Q ⇒ P: “Nếu tam giác ABC cân và có một góc bằng 60° thì tam giác ABC đều”.

Ta có một tam giác cân và có một góc bằng 60⁰ thì tam giác đó là tam giác đều.

Do đó mệnh đề Q ⇒ P đúng.

Do đó cả hai mệnh đề P ⇒ Q và Q ⇒ P đều là mệnh đề đúng.

Vậy ta có mệnh đề tương đương P ⇔ Q: “Tam giác ABC đều là điều kiện cần và đủ để tam giác ABC cân và có một góc bằng 60°”.

6. Kí hiệu ∀ và ∃

Giải Toán 10 trang 9 Tập 1

Hoạt động 7 trang 9 Toán lớp 10 Tập 1: Cho mệnh đề “n chia hết cho 3” với n là số tự nhiên.

a) Phát biểu “Mọi số tự nhiên n đều chia hết cho 3” có phải là mệnh đề không?

b) Phát biểu “Tồn tại số tự nhiên n chia hết cho 3” có phải là mệnh đề không?

Lời giải:

a) Phát biểu “Mọi số tự nhiên n đều chia hết cho 3” nói về một sự kiện toán học nên là một mệnh đề.

b) Phát biểu “Tồn tại số tự nhiên n chia hết cho 3” nói về một sự kiện toán học nên là một mệnh đề.

Giải Toán 10 trang 10 Tập 1

Hoạt động 8 trang 10 Toán lớp 10 Tập 1: Bạn An nói: “Mọi số thực đều có bình phương là một số không âm”.

Bạn Bình phủ định lại câu nói của bạn An: “Có một số thực mà bình phương của nó là một số âm”.

a) Sử dụng kí hiệu “$\forall$” để viết mệnh đề của bạn An.

b) Sử dụng kí hiệu “$\exists$” để viết mệnh đề của bạn Bình.

Lời giải:

a) Bằng cách sử dụng kí hiệu “$\forall$” mệnh đề của bạn An được viết: “$\forall x\in ℝ$, x² là một số không âm” hay “$\forall x\in ℝ$, x² ≥ 0”.

b) Bằng cách sử dụng kí hiệu “$\exists$” mệnh đề của bạn Bình được viết: “$\exists x\in ℝ$, x² là một số âm” hay “$\exists x\in ℝ$, x² < 0”.

Giải Toán 10 trang 11 Tập 1

Luyện tập 7 trang 11 Toán lớp 10 Tập 1: Phát biểu mệnh đề phủ định của mỗi mệnh đề sau:

a) Tồn tại số nguyên chia hết cho 3;

b) Mọi số thập phân đều viết được dưới dạng phân số.

Lời giải:

a) Mệnh đề phủ định của mệnh đề “Tồn tại số nguyên chia hết cho 3” là mệnh đề “Mọi số nguyên không chia hết cho 3”.

b) Mệnh đề phủ định của mệnh đề “Mọi số thập phân đều viết được dưới dạng phân số” là mệnh đề “Tồn tại số thập phân không viết được dưới dạng phân số”.

Bài tập

Bài 1 trang 11 Toán lớp 10 Tập 1: Trong các phát biểu sau, phát biểu nào là mệnh đề toán học?

a) Tích hai số thực trái dấu là một số thực âm.

b) Mọi số tự nhiên đều là số dương.

c) Có sự sống ngoài Trái Đất.

d) Ngày 1 tháng 5 là ngày Quốc tế Lao động.

Lời giải:

Phát biểu a) và b) là khẳng định về một sự kiện trong toán học nên hai phát biểu này là mệnh đề toán học.

Vậy phát biểu a) và b) là các mệnh đề toán học.

Bài 2 trang 11 Toán lớp 10 Tập 1: Lập mệnh đề phủ định của mỗi mệnh đề sau và nhận xét tính đúng sai của mệnh đề phủ định đó:

a) A: “ $\frac{5}{12}$ là một phân số”;

b) B: “Phương trình x² + 3x + 2 = 0 có nghiệm”;

c) C: “2² + 2³ = 2^{2 + 3}”;

d) D: “Số 2 025 chia hết cho 15”.

Lời giải:

a) Ta có: 1,2 $\notin Z$ nên $\frac{5}{1,2}$ không là một phân số. Vì vậy A là mệnh đề sai.

Mệnh đề phủ định của mệnh đề A là mệnh đề $\overline{A}$: “$\frac{5}{1,2}$ không phải là một phân số”, mệnh đề $\overline{A}$ phủ định này đúng do A sai.

b) Mệnh đề phủ định của mệnh đề B là mệnh đề $\overline{B}$: “Phương trình x² + 3x + 2 = 0 vô nghiệm”.

Ta có x² + 3x + 2 = 0 là phương trình bậc hai có ∆ = 3² – 4 . 1 . 2 = 9 – 8 = 1 > 0 nên phương trình có nghiệm, vậy mệnh đề B đúng nên mệnh đề $\overline{B}$ sai.

c) Mệnh đề phủ định của mệnh đề C là mệnh đề $\overline{C}$: “2² + 2³ ≠ 2^{2 + 3}”.

Ta có: 2² + 2³ = 4 + 8 = 12

2^{2 + 3} = 2⁵ = 32

Do đó 2² + 2³ ≠ 2^{2 + 3}

Vậy mệnh đề C sai và mệnh đề $\overline{C}$ đúng.

d) Mệnh đề phủ định của mệnh đề D là mệnh đề $\overline{D}$: “Số 2 025 không chia hết cho 15”.

Ta có: 2 025 : 15 = 135 nên 2 025 chia hết cho 15.

Suy ra mệnh đề D đúng nên mệnh đề phủ định $\overline{D}$ sai.

Bài 3 trang 11 Toán lớp 10 Tập 1: Cho n là số tự nhiên. Xét các mệnh đề:

P: “n là một số tự nhiên chia hết cho 16”;

Q: “n là một số tự nhiên chia hết cho 8”;

a) Phát biểu mệnh đề P ⇒ Q. Nhận xét tính đúng sai của mệnh đề đó.

b) Phát biểu mệnh đề đảo của mệnh đề P ⇒ Q. Nhận xét tính đúng sai của mệnh đề đó.

Lời giải:

a) Mệnh đề P ⇒ Q: “Nếu n là một số tự nhiên chia hết cho 16 thì n là một số tự nhiên chia hết cho 8”.

Ta có n chia hết cho 16 mà 16 = 2.8 nên chia hết cho 8. Do đó n chia hết cho 8.

Suy ra mệnh đề P ⇒ Q là mệnh đề đúng.

b) Mệnh đề đảo của mệnh đề P ⇒ Q là mệnh đề Q ⇒ P: “Nếu n là số tự nhiên chia hết cho 8 thì n là một số tự nhiên chia hết cho 16”.

Với n = 24 chia hết cho 8 nhưng 24 không chia hết cho 16. Do đó mệnh đề đảo này là mệnh đề sai.

Bài 4 trang 11 Toán lớp 10 Tập 1: Cho tam giác ABC. Xét các mệnh đề:

P: “Tam giác ABC cân”;

Q: “Tam giác ABC có hai đường cao bằng nhau”.

Phát biểu mệnh đề P ⇔ Q bằng bốn cách.

Lời giải:

Bốn cách để phát biểu mệnh đề P ⇔ Q như sau:

Cách 1: “Tam giác ABC cân điều kiện cần và đủ để có tam giác ABC có hai đường cao bằng nhau”.

Cách 2: “Tam giác ABC cân là khi và chỉ khi tam giác ABC có hai đường cao bằng nhau”.

Cách 3: “Tam giác ABC cân tương đương với tam giác ABC có hai đường cao bằng nhau”.

Cách 4: “Tam giác ABC cân nếu và chỉ nếu tam giác ABC có hai đường cao bằng nhau”.

Bài 5 trang 11 Toán lớp 10 Tập 1: Dùng kí hiệu “∀” hoặc “∃” để viết các mệnh đề sau:

a) Có một số nguyên không chia hết cho chính nó;

b) Mọi số thực cộng với 0 đều bằng chính nó.

Lời giải:

a) Sử dụng kí hiệu “$\exists$” mệnh đề đã cho được viết là: “$\exists x\in \mathbb{Z}$, x không chia hết cho x”.

b) Sử dụng kí hiệu “$\forall$” mệnh đề đã cho được viết là: “$\forall x\in ℝ$, x + 0 = x”.

Bài 6 trang 11 Toán lớp 10 Tập 1:

a) $\forall x\in ℝ$, x² ≥ 0;

b) $\exists x\in ℝ,\frac{1}{x}>x$.

Lời giải:

a) Mệnh đề “$\forall x\in ℝ$, x² ≥ 0” được phát biểu như sau: “Mọi số thực đều có bình phương không âm” hay “Mọi số thực đều có bình phương là một số lớn hơn hoặc bằng không”

b) Mệnh đề “$\exists x\in ℝ,\frac{1}{x}>x$” được phát biểu là: “Tồn tại số thực sao cho nghịch đảo của nó lớn hơn chính nó”.

Bài 7 trang 11 Toán lớp 10 Tập 1: Lập mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai của mỗi mệnh đề phủ định đó:

a) $\forall x\in ℝ$, x² ≠ 2x – 2;

b) $\forall x\in ℝ$, x² ≤ 2x – 1;

c) $\exists x\in ℝ,x+\frac{1}{x}\ge 2$;

d) $\exists x\in ℝ$, x² – x + 1 < 0.

Lời giải:

a) Phủ định của mệnh đề “$\forall x\in ℝ$, x² ≠ 2x – 2” là mệnh đề “$\exists x\in ℝ$, x² = 2x – 2”.

Ta xét phương trình x² = 2x – 2

⇔ x² – 2x + 2 = 0

Ta có: ∆' = (– 1)² – 1 . 2 = – 1 < 0

Do đó phương trình vô nghiệm trên tập số thực.

Nghĩa là không tồn tại số thực x thỏa mãn x² = 2x – 2 hay x² ≠ 2x – 2 với mọi số thực x.

Vậy mệnh đề phủ định trên là mệnh đề sai.

b) Phủ định của mệnh đề “$\forall x\in ℝ$, x² ≤ 2x – 1” là mệnh đề “$\exists x\in ℝ$, x² > 2x – 1”.

Với x = 3, ta có 3² = 9 và 2 . 3 – 1 = 6 – 1 = 5, vì 9 > 5 nên 3² > 2 . 3 – 1.

Suy ta tồn tại số thực x thỏa mãn x² > 2x – 1.

Vậy mệnh đề phủ định là mệnh đề đúng.

c) Phủ định của mệnh đề “$\exists x\in ℝ,x+\frac{1}{x}\ge 2$” là mệnh đề “$\forall x\in ℝ,x+\frac{1}{x}<2$”.

Ta thấy với x = 10, ta thấy $10+\frac{1}{10}=10,1$ > 2.

Vậy mệnh đề phủ định là mệnh đề sai.

d) Phủ định của mệnh đề “$\exists x\in ℝ$, x² – x + 1 < 0” là mệnh đề “$\forall x\in ℝ$, x² – x + 1 ≥ 0”.

Ta có: x² – x + 1

= $x^2-2.x.\frac{1}{2}+{\left(\frac{1}{2}\right)}^2+\frac{3}{4}$

$={\left(x-\frac{1}{2}\right)}^2+\frac{3}{4}>0\forall x\in ℝ$

⇒ x² – x + 1 ≥ 0 $\forall x\in ℝ$

Mệnh đề phủ định này là mệnh đề đúng.

Lý thuyết Bài 1: Mệnh đề toán học

1. Mệnh đề toán học

• Mệnh đề toán học là mệnh đề khẳng định một sự kiện trong toán học.

Ví dụ:

+ “Hà Nội là thủ đô của Việt Nam” không phải một sự kiện toán học. Do đó khẳng định này không phải mệnh đề toán học.

+ “Số π là một số hữu tỉ” là khẳng định một sự kiện trong toán học. Do đó khẳng định này là một mệnh đề toán học.

• Mỗi mệnh đề toán học phải đúng hoặc sai, không thể vừa đúng, vừa sai.

- Khi mệnh đề toán học là đúng, ta gọi mệnh đề đó là một mệnh đề đúng.

- Khi mệnh đề toán học là sai, ta gọi mệnh đề đó là một mệnh đề sai.

Ví dụ:

+ “Tổng ba góc trong tam giác bằng 180⁰” là một mệnh đề đúng.

+ “$\sqrt{2}$ là số hữu tỉ” là một mệnh đề sai (vì $\sqrt{2}\approx 1,\mathrm{414213562...}$là một số vô tỉ).

2. Mệnh đề chứa biến

• Ở mệnh đề chứa biến, ta chưa thể khẳng định ngay tính đúng hoặc sai. Với mỗi giá trị cụ thể của biến số, ta có một mệnh đề toán học mà ta có thể khẳng định tính đúng hoặc sai của mệnh đề.

Kí hiệu mệnh đề chứa biến n là P(n), mệnh đề chứa biến x, y là P(x, y), …

Ví dụ:

+ P(x): “x là một số nguyên tố” là một mệnh đề chứa biến

Với x = 3, mệnh đề P(x): “3 là một số nguyên tố” là mệnh đề đúng.

Với x = 8, mệnh đề P(x): “8 là một số nguyên tố” là mệnh đề sai.

3. Phủ định của một mệnh đề

• Cho mệnh đề P. Mệnh đề “Không phải P” được gọi là mệnh đề phủ định của mệnh đề P và kí hiệu là $\overline{P}$.

Mệnh đề $\overline{P}$ đúng khi P sai, và ngược lại.

Ví dụ:

+ A: “69420 là một số lẻ” là mệnh đề sai.

Mệnh đề phủ định $\overline{A}$: “69420 không phải một số lẻ”, $\overline{A}$ là mệnh đề đúng.

Chú ý: Để phủ định một mệnh đề, ta chỉ cần thêm (hoặc bớt) từ “không” (hoặc “không phải”) vào trước vị ngữ của mệnh đề đó.

4. Mệnh đề kéo theo

• Cho hai mệnh đề P và Q. Mệnh đề “Nếu P thì Q” được gọi là mệnh đề kéo theo, được kí hiệu là P ⇒ Q.

Mệnh đề P ⇒ Q chỉ sai khi P đúng Q sai, và đúng trong tất cả các trường hợp còn lại.

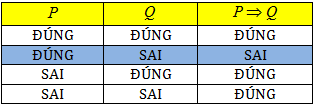
Nhận xét: Tùy theo nội dung cụ thể, đôi khi người ta còn phát biểu mệnh đề P ⇒ Q là “P kéo theo Q” hay “P suy ra Q” hay “Vì P nên Q”…

Ví dụ:

+ Xét hai mệnh đề: P: “Tứ giác ABCD có bốn cạnh bằng nhau” và Q: “Tứ giác ABCD là hình thoi”.

+ Mệnh đề P ⇒ Q được phát biểu là: “Nếu tứ giác ABCD có bốn cạnh bằng nhau thì tứ giác ABCD là hình thoi”. Mệnh đề này là mệnh đề đúng.

Nhận xét: Các định lí toán học thường phát biểu ở dạng mệnh đề kéo theo P ⇒ Q.

Khi đó ta nói:

P là giả thiết, Q là kết luận của định lí, hay P là điều kiện đủ để có Q, hoặc Q là điều kiện cần để có P.

Ví dụ:

Ta có định lý: Nếu một tứ giác có tổng số đo hai góc đối diện nhau bằng 180⁰ thì tứ giác đó nội tiếp được đường tròn.

Khi đó, ta nói:

+ Tứ giác có tổng số đo hai góc đối diện nhau bằng 180⁰ là điều kiện đủ để tứ giác đó nội tiếp được đường tròn.

+ Tứ giác đó nội tiếp được đường tròn là điều kiện cần để tứ giác có tổng số đo hai góc đối diện nhau bằng 180⁰.

5. Mệnh đề đảo. Mệnh đề tương đương

• Mệnh đề Q ⇒ P là mệnh đề đảo của mệnh đề P ⇒ Q.

Nếu cả hai mệnh đề P ⇒ Q và Q ⇒ P đều đúng, P và Q là hai mệnh đề tương đương và kí hiệu P ⇔ Q.

Nhận xét: Mệnh đề P ⇔ Q có thể phát biểu ở những dạng như sau:

+ “P tương đương Q”;

+ “P là điều kiện cần và đủ để có Q”;

+ “P khi và chỉ khi Q”;

+ “P nếu và chỉ nếu Q”.

Ví dụ: Với P: “Tứ giác ABCD có bốn cạnh bằng nhau” và Q: “Tứ giác ABCD là hình thoi” thì P ⇒ Q: “Tứ giác ABCD có bốn cạnh bằng nhau thì tứ giác ABCD là hình thoi” là mệnh đề đúng, và Q ⇒ P: “Nếu tứ giác ABCD là hình thoi thì tứ giác ABCD có bốn cạnh bằng nhau” cũng là mệnh đề đúng.

Do đó P ⇔ Q, phát biểu:

+ “Tứ giác ABCD là hình thoi khi và chỉ khi tứ giác ABCD có bốn cạnh bằng nhau”.

+ “Tứ giác ABCD là hình thoi là điều kiện cần và đủ để tứ giác ABCD có bốn cạnh bằng nhau”.

Chú ý: Trong toán học, những câu khẳng đỉnh đúng phát biểu ở dạng “P ⇔ Q” cũng được coi là một mệnh đề toán học, gọi là mệnh đề tương đương.

6. Kí hiệu ∀ và ∃

• Kí hiệu ∀ đọc là “với mọi”.

• Kí hiệu ∃ đọc là “tồn tại”, hoặc “có một” (tồn tại một), hoặc “có ít nhất một” (tồn tại ít nhất một).

Ví dụ: Phát biểu các mệnh đề:

+ “$\forall x\in ℝ,x^2+1>0$”: Với mọi số thực x thì x² + 1 luôn lớn hơn 0.

+ “$\exists x\in \mathbb{N},2x=3$”: Tồn tại số tự nhiên x sao cho 2x bằng 3.

• Phủ định của mệnh đề “$\forall x\in X,P\left(x\right)$” là mệnh đề “$\exists x\in X,\overline{P\left(x\right)}$”.

• Phủ định của mệnh đề “$\exists x\in X,P\left(x\right)$” là mệnh đề “$\forall x\in X,\overline{P\left(x\right)}$”.

Ví dụ:

+ Phủ định của mệnh đề “$\forall x\in ℝ,x^2+1>0$” là mệnh đề “$\exists x\in ℝ,x^2+1\le 0$”.

+ Phủ định của mệnh đề “$\exists x\in \mathbb{N},2x=3$” là mệnh đề “$\forall x\in \mathbb{N},2x\ne 3$”.

Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

Bài 2: Tập hợp. Các phép toán trên tập hợp

Bài tập cuối chương 1

Bài 1: Bất phương trình bậc nhất hai ẩn

Bài 2: Hệ bất phương trình bậc nhất hai ẩn

Bài tập cuối chương 2

Xem thêm tài liệu Toán lớp 10 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 1. Mệnh đề toán học