Giải Toán 10 Bài 1 (Cánh diều): Bất phương trình bậc nhất hai ẩn

Giải bài tập Toán 10 Bài 1: Bất phương trình bậc nhất hai ẩn

Video giải bài tập Toán 10 Bài 1: Bất phương trình bậc nhất hai ẩn

Giải Toán 10 trang 20 Tập 1

Câu hỏi khởi động trang 20 Toán lớp 10 Tập 1: Nhân dịp Tết Trung thu, một doanh nghiệp dự định sản xuất hai loại bánh: bánh nướng và bánh dẻo. Lượng đường cần cho mỗi chiếc bánh nướng, bánh dẻo lần lượt là 60 g, 50 g. Doanh nghiệp đã nhập về 500 kg đường.

Số bánh nướng và số bánh dẻo doanh nghiệp dự định sản xuất cần thỏa mãn điều kiện ràng buộc gì để lượng đường sản xuất bánh không vượt quá lượng đường đã nhập về?

Lời giải:

Sau bài học này ta sẽ giải quyết đc bài toán này như sau:

Gọi số bánh nướng mà doanh nghiệp dự định sản xuất là x (bánh) và số bánh dẻo mà doanh nghiệp dự định sản xuất là y (bánh) (x, y $\in {\mathbb{N}}^{*}$).

Lượng đường cần cho x chiếc bánh nướng là: 50x (g)

Lượng đường cần cho y chiếc bánh dẻo là: 60y (g)

Tổng lượng đường cần dùng là: 50x + 60y (g)

Lượng đường công ty đã nhập là: 500 kg = 500 000 g.

Để lượng đường sản xuất bánh không vượt quá số đường doanh nghiệp đã nhập về, ta có: 50x + 60y ≤ 500 000.

Vậy điều kiện ràng buộc đối với x và y là: 0,06x + 0,05y ≤ 500. Đây được gọi là bất phương trình bậc nhất hai ẩn.

Hoạt động 1 trang 20 Toán lớp 10 Tập 1: Trong bài toán ở phần mở đầu, ta gọi x, y lần lượt là số bánh nướng và số bánh dẻo doanh nghiệp dự định sản xuất (x, y là số tự nhiên). Nêu điều kiện ràng buộc đối với x và y để lượng đường sản xuất bánh không vượt quá lượng đường đã nhập về.

Lời giải:

Quan sát bài toán mở đầu, ta thấy số lượng đường nhập về và lượng đường cần để làm cho mỗi chiếc bánh chưa đưa về cùng đơn vị, do đó ta cần đổi đơn vị đo khối lượng.

Đổi: 60 g = 0,06 kg; 50 g = 0,05 kg.

Lượng đường cần dùng để làm x chiếc bánh nướng là: 0,06x (kg).

Lượng đường cần dùng để làm y chiếc bánh dẻo là: 0,05y (kg).

Tổng số đường để làm số bánh nướng và bánh dẻo mà công ti dự định sản xuất là: 0,06x + 0,05y (kg)

Vì doanh nghiệp nhập về 500 kg đường, nên tổng số đường cần để làm các loại bánh theo dự định phải không quá 500 kg.

Vậy điều kiện ràng buộc đối với x và y là: 0,06x + 0,05y ≤ 500.

Giải Toán 10 trang 21 Tập 1

Luyện tập 1 trang 21 Toán lớp 10 Tập 1: Tìm bất phương trình bậc nhất hai ẩn trong các bất phương trình sau và chỉ ra một nghiệm của bất phương trình bậc nhất hai ẩn đó:

a) 5x + 3y < 20;

b) 3x – $\frac{5}{y}$> 2.

Lời giải:

+ Bất phương trình a) 5x + 3y < 20 có dạng ax + by < 20 với a = 5, b = 3 và c = 20 nên là bất phương trình bậc nhất hai ẩn.

+ Để chỉ ra nghiệm của bất phương trình bậc nhất hai ẩn trên, ta chỉ cần chọn cặp số (x₀; y₀) thỏa mãn 5x₀ + 3y₀ < 20.

Chọn x₀ = -2, y₀ = 3, ta có: 5 . (-2) + 3 . 3 = -1 < 20 (thỏa mãn)

Vậy (-2; 3) là một nghiệm của của bất phương trình bậc nhất hai ẩn 5x + 3y < 20.

Hoạt động 2 trang 21 Toán lớp 10 Tập 1: Trong mặt phẳng tọa độ Oxy, xác định các điểm M(x; y) mà:

a) x > 0 (1);

b) y < 1 (2).

Lời giải:

Để xác định điểm M(x; y) trong mặt phẳng tọa độ thỏa mãn điều kiện đã cho, ta làm như sau:

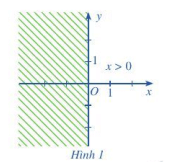
a) Đường thẳng x = 0 chính là trục tung.

Đường thẳng x = 0 chia mặt phẳng tọa độ thành 2 nửa: nửa mặt phẳng bên trái và nửa mặt phẳng bên phải trục tung.

Lấy điểm M bất kì nằm ở nửa mặt phẳng bên phải, ta thấy hoành độ của điểm M luôn thỏa mãn lớn hơn 0 nên tọa độ điểm M là nghiệm bất phương trình (1).

Vì vậy, miền nghiệm của bất phương trình (1) là nửa mặt phẳng bên phải trục tung (không kể trục tung) phần nửa mặt phẳng còn lại không phải miền nghiệm của bất phương trình (1) nên ta sẽ gạch bỏ như hình vẽ.

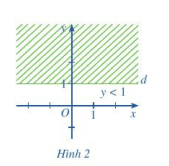
b) Vẽ đường thẳng y = 1.

Đường thẳng d: y = 1 chia mặt phẳng thành hai nửa: nửa mặt phẳng bên trên và nửa mặt phẳng bên dưới đường thẳng d (không kể đường thẳng d).

Lấy điểm M bất kì nằm ở nửa mặt phẳng bên dưới đường thẳng d, ta thấy tung độ của điểm M luôn thỏa mãn nhỏ hơn 1 nên tọa độ điểm M là nghiệm bất phương trình (2).

Vì vậy, miền nghiệm của bất phương trình (2) là nửa mặt phẳng bên dưới đường thẳng d (không kể đường thẳng d) phần nửa mặt phẳng còn lại không phải miền nghiệm của bất phương trình (2) nên ta sẽ gạch bỏ như hình vẽ.

Giải Toán 10 trang 22 Tập 1

Hoạt động 3 trang 22 Toán lớp 10 Tập 1: Cho bất phương trình 2x – y > 2 (3).

a) Trong mặt phẳng tọa độ Oxy, vẽ đường thẳng d: 2x – y = 2 ⇔ y = 2x – 2.

b) Xét điểm M(2; – 1). Chứng tỏ (2; – 1) là nghiệm của bất phương trình (3).

c) Đường thẳng d chia mặt phẳng tọa độ thành hai nửa mặt phẳng. Gạch đi nửa mặt phẳng không chứa điểm M(2; – 1).

Lời giải:

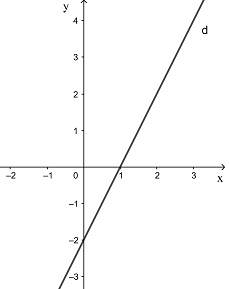
a) Đường thẳng d: y = 2x – 2

Ta có bảng sau:

Đồ thi hàm số đã cho là đường thẳng d đi qua hai điểm (0; – 2) và (1; 0):

b) Xét điểm M(2; – 1).

Thay x = 2 và y = – 1 vào bất phương trình (3) ta được: 2 . 2 – (– 1) > 2 ⇔ 5 > 2 (luôn đúng).

Vậy (2; – 1) là nghiệm của bất phương trình (3).

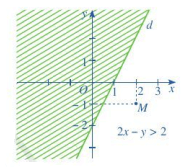
c) Gạch đi nửa mặt không chứa điểm M(2;-1), ta được hình vẽ sau:

Miền nghiệm của bất phương trình (3) là nửa mặt phẳng không bị gạch trong hình trên.

Giải Toán 10 trang 24 Tập 1

Luyện tập 2 trang 24 Toán lớp 10 Tập 1: Biểu diễn miền nghiệm của mỗi bất phương trình sau:

a) x – 2y < 4;

b) x + 3y ≤ 6.

Lời giải:

a)

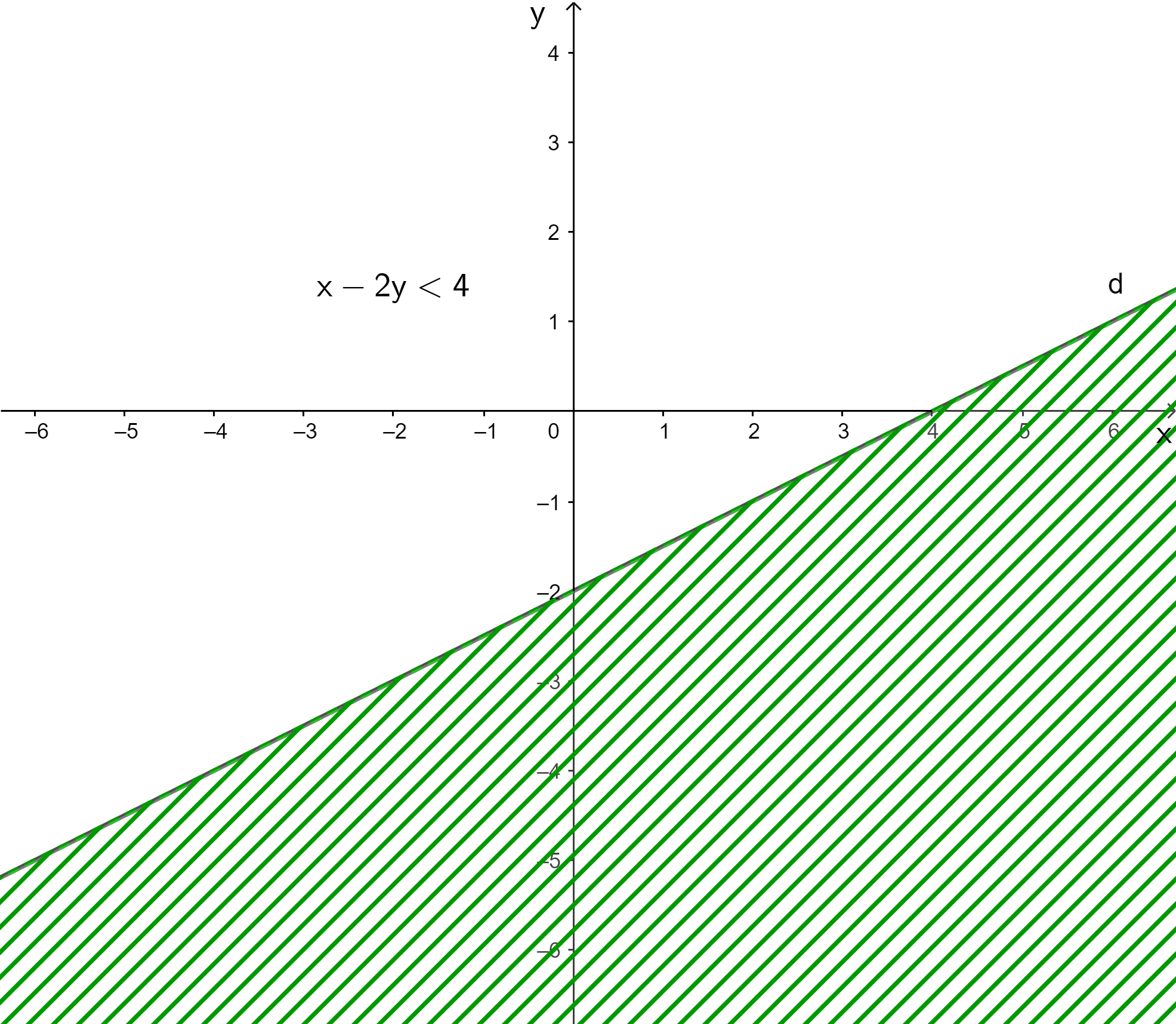
+ Vẽ đường thẳng d: x – 2y = 4 ⇔ y = $\frac{1}{2}$x – 2

Ta có bảng sau:

Đồ thị hàm số y = $\frac{1}{2}$x – 2 là đường thẳng d đi qua 2 điểm (0; – 2) và (4; 0).

+ Lấy điểm O(0; 0). Ta có: 0 – 2.0 = 0 < 4.

Vậy miền nghiệm của bất phương trình x – 2y < 4 là nửa mặt phẳng không bị gạch ở hình trên chứa điểm O(0; 0) không kể đường thẳng d.

b)

+ Vẽ đường thẳng d: x + 3y = 6 ⇔ y = $-\frac{1}{3}x+2$.

Ta có bảng sau:

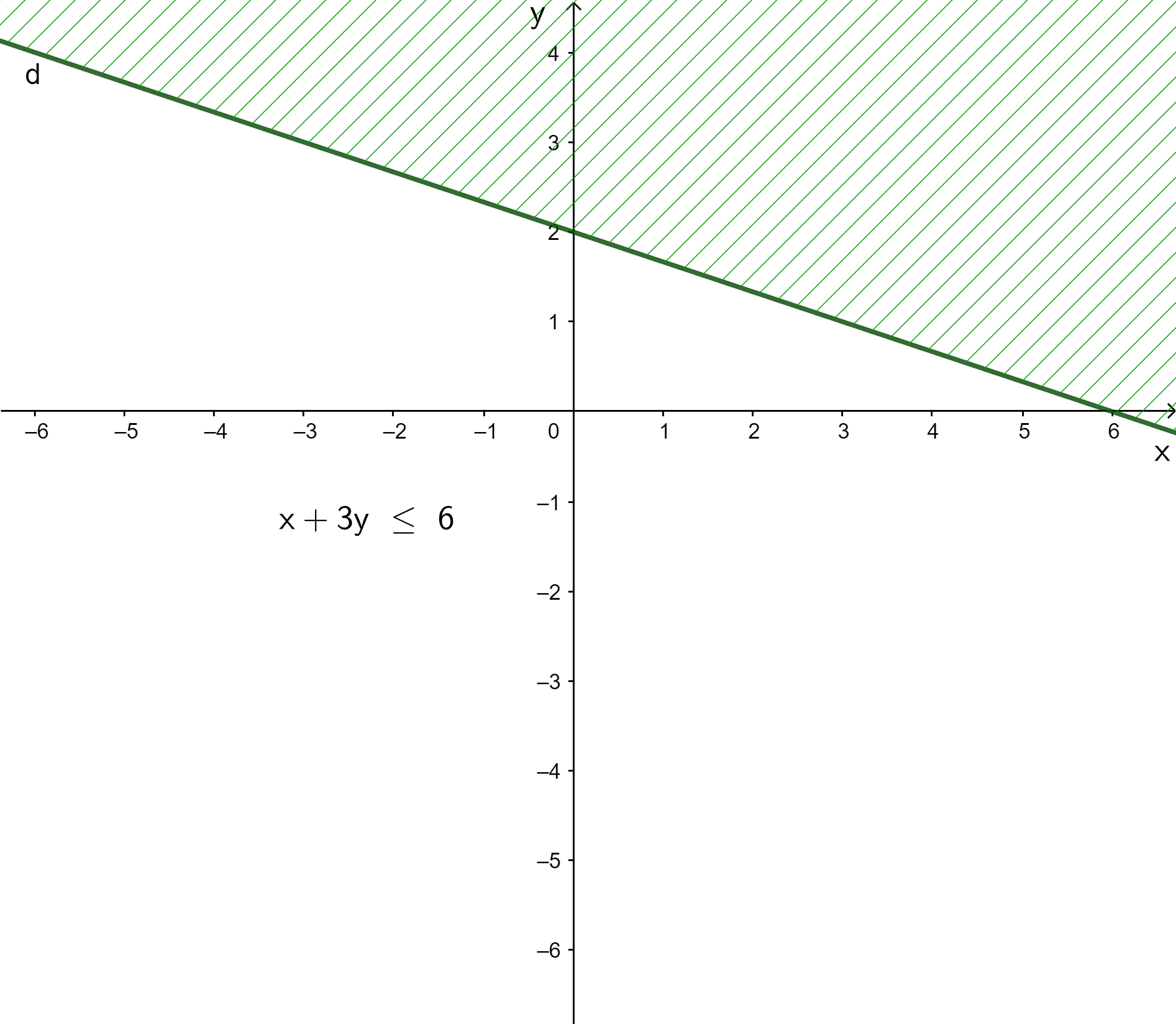
Đồ thị của hàm số là đường thẳng d đi qua hai điểm (0; 2) và (6; 0).

+ Lấy điểm O(0; 0). Ta có: 0 + 3.0 = 0 < 6.

Vậy miền nghiệm của bất phương trình x + 3y ≤ 6 là nửa mặt phẳng không bị gạch ở hình trên chứa điểm O(0; 0) kể cả đường thẳng d.

Bài tập

Bài 1 trang 24 Toán lớp 10 Tập 1: Cặp số nào sau đây là nghiệm của bất phương trình 2x – 3y < 3?

a) (0; – 1);

b) (2; 1);

c) (3; 1).

Lời giải:

a) Thay x = 0, y = – 1 vào vế trái của bất phương trình đã cho, ta được:

2.0 – 3.(-1) = 0 + 3 = 3

Mà 3 = 3 do đó cặp số (0;-1) không thỏa mãn bất phương trình đã cho hay cặp số (0;-1) không là nghiệm của bất phương trình 2x – 3y < 3.

Vậy cặp số (0;-1) không là nghiệm của bất phương trình 2x – 3y < 3.

b) Thay x = 2, y = 1 vào vế trái của bất phương trình đã cho, ta được:

2.2 – 3.1 = 4 – 3 = 1

Mà 1 < 3 do đó cặp số (2; 1) thỏa mãn bất phương trình đã cho hay cặp số (2; 1) là nghiệm của bất phương trình 2x – 3y < 3.

Vậy cặp số (2; 1) là nghiệm của bất phương trình 2x – 3y < 3.

c) Thay x = 3, y = 1 vào vế trái của bất phương trình đã cho, ta được:

2.3 – 3.1 = 6 – 3 = 3

Mà 3 = 3 do đó cặp số (3; 1) thỏa mãn bất phương trình đã cho hay cặp số (3; 1) là nghiệm của bất phương trình 2x – 3y < 3.

Vậy cặp số (3; 1) là nghiệm của bất phương trình 2x – 3y < 3.

Bài 2 trang 24 Toán lớp 10 Tập 1: Biểu diễn miền nghiệm của mỗi bất phương trình sau:

a) x + 2y < 3;

b) 3x – 4y ≥ – 3;

c) y ≥ – 2x + 4;

d) y < 1 – 2x.

Lời giải:

a)

+ Vẽ đường thẳng d₁: x + 2y = 3 ⇔ y = $-\frac{1}{2}x+\frac{3}{2}$.

Ta có bảng sau:

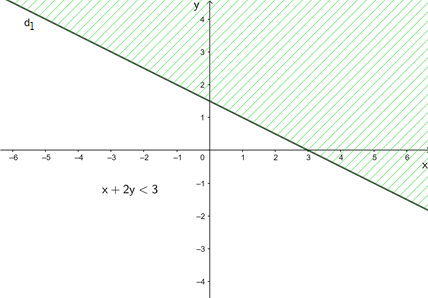
Đồ thị hàm số là đường thẳng d₁ đi qua điểm (1; 1) và (3; 0).

+ Lấy điểm O(0; 0). Ta có: 0 + 2.0 = 0 < 3.

Vậy miền nghiệm của bất phương trình x + 2y < 3 là nửa mặt phẳng không bị gạch ở hình trên chứa điểm O(0; 0) không kể đường thẳng d₁.

+ Vẽ đường thẳng d₂: 3x – 4y = – 3 ⇔ y = $\frac{3}{4}x+\frac{3}{4}$.

Ta có bảng sau:

+ Lấy điểm O(0; 0). Ta có: 3.0 – 4.0 = 0 > – 3.

+ Vậy miền nghiệm của bất phương trình 3x – 4y ≥ – 3 là nửa mặt phẳng không bị gạch ở hình trên chứa điểm O(0; 0) kể cả đường thẳng d₂.

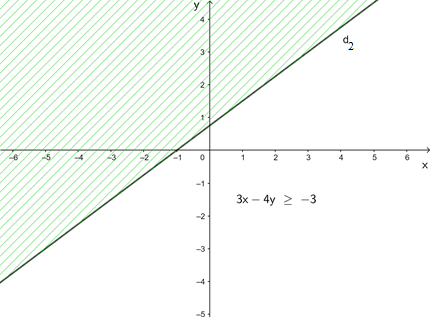
c) y ≥ – 2x + 4 ⇔ 2x + y ≥ 4

+ Vẽ đường thẳng d₃: 2x + y = 4 ⇔ y = - 2x + 4

Ta có bảng sau:

Đồ thị hàm số là đường thẳng d₃ đi qua các điểm có tọa độ (0;4) và (2;0).

+ Lấy điểm O(0; 0). Ta có: 2 . 0 + 0 = 0 < 4.

Vậy miền nghiệm của bất phương trình 2x + y ≥ 4 hay chính là y ≥ – 2x + 4 là nửa mặt phẳng không bị gạch ở hình trên không chứa điểm O(0; 0) kể cả đường thẳng d₃.

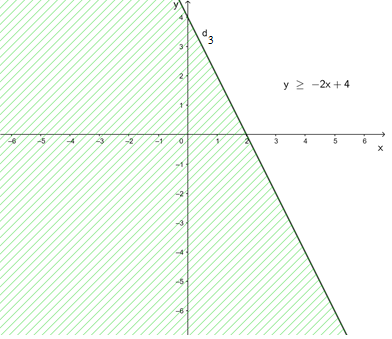
d) y < 1 – 2x ⇔ 2x + y < 1

+ Vẽ đường thẳng d₄: 2x + y = 1 ⇔ y = -2x + 1

Ta có bảng sau:

Đồ thị hàm số là đường thẳng d₄ đi qua các điểm có tọa độ (0; 1) và (1; -1).

+ Lấy O(0; 0). Ta có: 2 . 0 + 0 = 0 < 1.

+ Vậy miền nghiệm của bất phương trình 2x + y < 1 hay chính là y < 1 – 2x là nửa mặt phẳng không bị gạch ở hình trên chứa điểm O(0; 0) không kể đường thẳng d₄.

Bài 3 trang 24 Toán lớp 10 Tập 1: Phần không gạch (không kể d) ở mỗi Hình 7a, 7b, 7c là miền nghiệm của bất phương trình nào?

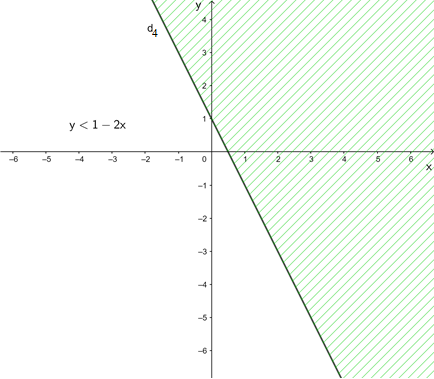
Lời giải:

a) Gọi phương trình đường thẳng d có dạng: y = ax + b (1) (a ≠ 0)

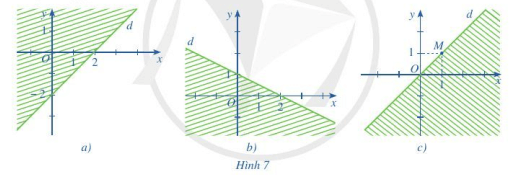
Quan sát Hình 7a, ta thấy đường thẳng d đi qua hai điểm (0; – 2) và (2; 0).

Thay x = 0, y = – 2 vào (1) ta được: – 2 = a.0 + b hay b = – 2

Thay x = 2, y = 0 vào (1) ta được: 0 = 2a + b

Mà b = -2 nên 0 = 2a – 2 ⇔ a = 1 (thỏa mãn)

⇒ d: y = x – 2 ⇔ x – y = 2

Ta thấy miền nghiệm của bất phương trình cần tìm không chứa điểm O(0; 0)

Mặt khác khi thay tọa độ của điểm O(0; 0) vào vế trái của phương trình đường thẳng d ta thấy 0 – 0 = 0 < 2.

Hơn nữa miền nghiệm không kể đường thẳng d nên ta có bất phương trình: x – y > 2.

Vậy phần không gạch (không kể d) là miền nghiệm của bất phương trình x – y > 2.

b) Gọi phương trình đường thẳng d có dạng: y = ax + b (2) (a ≠ 0)

Quan sát Hình 7b, ta thấy đường thẳng d đi qua 2 điểm (0; 1) và (2; 0).

Thay x = 0, y = 1 vào (2), ta được: 1 = a.0 + b ⇔ b = 1.

Thay x = 2, y = 0 vào (2), ta được: 2a + b = 0

Mà b = 1 nên 2a + 1 = 0 ⇔ a = $-\frac{1}{2}$ (t/m)

⇒ d: y = $-\frac{1}{2}$x + 1 ⇔ x + 2y = 2

Ta thấy miền nghiệm của bất phương trình cần tìm không chứa điểm O(0; 0)

Mặt khác khi thay tọa độ của điểm O(0; 0) vào vế trái của phương trình đường thẳng d ta thấy 0 + 2.0 = 0 < 2.

Hơn nữa miền nghiệm không kể đường thẳng d nên ta có bất phương trình: x + 2y > 2.

Vậy phần không gạch sọc (không kể d) là miền nghiệm của bất phương trình x + 2y > 2.

c) Gọi phương trình đường thẳng d có dạng: y = ax + b (a ≠ 0) (3)

Quan sát Hình 7c, ta thấy đường thẳng d đi qua gốc tọa độ và đi qua điểm M(1; 1):

Thay x = 0, y = 0 vào (3), ta được: 0 = a.0 + b ⇔ b = 0.

Thay x = 1, y = 1 vào (3), ta được: 1 = a.1 + b

Mà b = 0 nên 1 = a hay a = 1 (t/m)

⇒ d: y = x ⇔ x – y = 0

Xét điểm có tọa độ (0; 1). Ta có: = 0 – 1 = -1 < 0.

Lại có trên Hình 7c điểm (0; 1) nằm trên miền nghiệm của bất phương trình nên bất phương trình cần tìm là x – y < 0.

Vậy phần không gạch sọc (không kể d) là miền nghiệm của bất phương trình x – y < 0.

Bài 4 trang 24 Toán lớp 10 Tập 1: Một gian hàng trưng bày bàn và ghế rộng 60 m². Diện tích để kê một chiếc ghế là 0,5 m², một chiếc bàn là 1,2 m². Gọi x là số chiếc ghế, y là số chiếc bàn được kê.

a) Viết bất phương trình bậc nhất hai ẩn x, y cho phần mặt sàn để kê bàn và ghế biết diện tích mặt sàn dành cho lưu thông tối thiểu là 12m².

b) Chỉ ra ba nghiệm của bất phương trình trên.

Lời giải:

a) Vì x là số chiếc ghế và y là số chiếc bàn được kê nên ta có điều kiện: $x,y\in \mathbb{N}$

Vì diện tích mặt sàn dành cho lưu thông tối thiểu là 12 m², do đó diện tích phần mặt sàn để kê bàn và ghế tối đa là: 60 – 12 = 48 (m²).

Diện tích để kê x chiếc ghế là 0,5x (m²).

Diện tích để kê y chiếc bàn là 1,2y (m²).

Tổng diện tích cho phần mặt sàn để kê x chiếc ghế và y chiếc bàn là: 0,5x + 1,2y (m²).

Vì tổng diện tích mặt sàn để kê bàn và ghế tối đa là 48m² nên ta có bất phương tình: 0,5x + 1,2y ≤ 48.

Vậy bất phương trình cần tìm là: 0,5x + 1,2y ≤ 48.

b) Gọi cặp số (x₀; y₀) là nghiệm của bất phương trình 0,5x + 1,2y ≤ 48 (x₀, y₀ là các số tự nhiên).

⇒ 0,5x₀ + 1,2y₀ ≤ 48

Ba cặp số (x₀; y₀) thỏa mãn điểu kiện 0,5x₀ + 1,2y₀ ≤ 48 là:

+ Chọn x₀ = 1, y₀ = 4, ta có: 0,5 . 1 + 1,2 . 4 = 0,5 + 4,8 = 5,3 < 48.

+ Chọn x₀ = 10, y₀ = 10, ta có: 0,5 . 10 + 1,2 . 10 = 5 + 12 = 17 < 48.

+ Chọn x₀ = 20, y_0­ = 5, ta có: 0,5 . 20 + 1,2 . 5 = 10 + 6 = 16 < 48.

Vậy ba cặp số (1; 4), (10; 10), (20; 5) là ba nghiệm của bất phương trình 0,5x + 1,2y ≤ 48.

Bài 5 trang 24 Toán lớp 10 Tập 1: Trong 1 lạng (100 g) thịt bò chứa khoảng 26 g protein, 1 lạng cá rô phi chứa khoảng 20 g protein. Trung bình mỗi ngày, một người phụ nữ cần tối thiểu 46 g protein. (Nguồn: https://vinmec.com và https://thanhnien.vn) Gọi x, y lần lượt là số lạng thịt bò và số lạng cá rô phi mà một người phụ nữ nên ăn trong một ngày. Viết bất phương trình bậc nhất hai ẩn x, y để biểu diễn lượng protein cần thiết cho một người phụ nữ trong một ngày và chỉ ra ba nghiệm của bất phương trình đó.

Lời giải:

Vì x, y là số lạng thịt bò và số lạng cá rô phi cần tối thiểu trong một ngày nên điều kiện x, y ≥ 0.

Trong x lạng thịt bò chứa khoảng 26x (g protein).

Trong y lạng cá rô phi chứa khoảng 20y (g protein).

Tổng số lượng protein mà một người phụ nữ nên ăn trong một ngày là: 26x + 20y (g protein).

Vì trung bình mỗi ngày, một người phụ nữ cần tối thiểu 46 g protein nên ta có bất phương trình là: 26x + 20y ≥ 46.

Vậy bất phương trình bậc nhất hai ẩn x, y để biểu diễn lượng protein cần thiết cho một người phụ nữ trong một ngày là: 26x + 20y ≥ 46.

Cặp số (x₀; y₀) là nghiệm của bất phương trình 26x + 20y ≥ 46 nếu thỏa mãn 26x₀ + 20y₀ ≥ 46 và x₀, y₀ ≥ 0.

+ Chọn x₀ = 0, y₀ = 3, ta có: 26 . 0 + 20 . 3 = 60 > 46

+ Chọn x₀ = 1,5, y₀ = 1, ta có: 26 . 1,5 + 20 . 1 = 59 > 46

+ Chọn x₀ = 2,2, y₀ = 1,3, ta có: 26 . 2,2 + 20 . 1,3 = 83,2 > 46

Vậy ba cặp số (0; 3), (1,5; 1), (2,2; 1,3) là ba nghiệm của bất phương trình 26x + 20y ≥ 46.

Lý thuyết Bất phương trình bậc nhất hai ẩn

1. Bất phương trình bậc nhất hai ẩn

• Bất phương trình bậc nhất hai ẩn x, y là bất phương trình có một trong các dạng sau:

ax + by < c; ax + by > c

ax + by ≤ c; ax + by ≥ c

trong đó:

x, y là các ẩn,

a, b, c là các số thực cho trước với a, b không đồng thời bằng 0.

Ví dụ:

+) $\frac{5}{3}x+\sqrt{2}y<5$ có dạng bất phương trình bậc nhất hai ẩn x và y với $a=\frac{5}{3}$, $b=\sqrt{2}$ và c = 5.

+ $3x-\frac{5}{y}\ge 2$ không phải bất phương trình bậc nhất hai ẩn, vì không có dạng bất phương trình bậc nhất hai ẩn.

• Cho bất phương trình bậc nhất hai ẩn ax + by < c (*).

Mỗi cặp số (x₀ ; y₀) sao cho ax₀ + by₀ < c gọi là một nghiệm của bất phương trình (*).

Trong mặt phẳng toạ độ Oxy, tập hợp tất cả các điểm có toạ độ là nghiệm của bất phương trình (*) được gọi là miền nghiệm của bất phương trình đó.

Nghiệm và miền nghiệm của các bất phương trình dạng ax + by > c; ax + by ≤ c và ax + by ≥ c được định nghĩa tương tự.

Ví dụ: Xét bất phương trình 2x + y ≤ 3:

+ (1 ; 1) là một nghiệm của bất phương trình vì 2 . 1 + 1 = 3 ≤ 3 là mệnh đề đúng.

+ (–2 ; 10) không là nghiệm của bất phương trình vì 2 . (–2) + 10 = 6 ≤ 3 là mệnh đề sai.

+ (2 ; –5) là nghiệm của bất phương trình vì 2 . 2 – 5 = –1 ≤ 3 là mệnh đề đúng.

2. Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn

• Trong mặt phẳng toạ độ Oxy, đường thẳng d: ax + by = c chia mặt phẳng thành hai nửa mặt phẳng. Một trong hai nửa mặt phẳng (không kể d) là miền nghiệm của bất phương trình ax + by < c, nửa mặt phẳng còn lại (không kể d) là miền nghiệm của bất phương trình ax + by > c.

Chú ý: Đối với bất phương trình dạng ax + by ≤ c hoặc ax + by ≥ c thì miền nghiệm là nửa mặt phẳng kể cả đường thẳng d.

Ví dụ: Đường thẳng d: 2x – 3y = 6 chia mặt phẳng Oxy thành hai nửa mặt phẳng như hình dưới. Hỏi nửa mặt không bị gạch (không kể đường thẳng d) là miền nghiệm của bất phương trình nào?

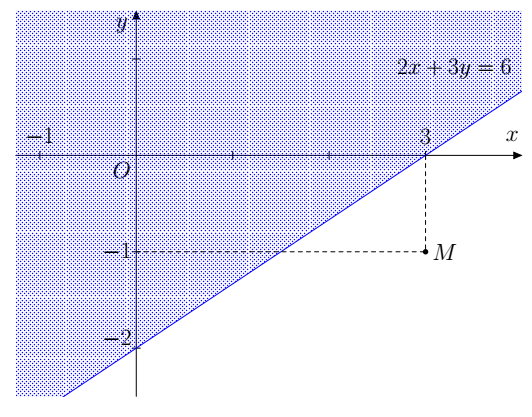
Hướng dẫn giải:

Lấy một giá trị nằm trong nửa mặt phẳng không bị gạch, ví dụ điểm M(3 ; –1). Thay toạ độ điểm M vào vế trái phương trình đường thẳng d, ta thấy:

2x_M – 3y_M = 2 . 3 – 3 . (–1) = 9 > 6

Như vậy, M là một nghiệm của bất phương trình 2x – 3y > 6, miền không bị gạch (không kể d) là miền nghiệm của bất phương trình 2x – 3y > 6.

Vậy miền không bị gạch (không kể đường thẳng d) là miền nghiệm của bất phương trình 2x – 3y > 6.

• Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn:

Bước 1. Vẽ đường thẳng d: ax + by = c. Đường thẳng d chia mặt phẳng toạ độ thành hai nửa mặt phẳng.

Bước 2. Lấy một điểm M(x₀; y₀) không nằm trên d (thường lấy gốc toạ độ O nếu c ≠ 0). Tính ax₀ + by₀ và so sánh với c.

Bước 3. Kết luận:

+) Nếu ax₀ + by₀ < c thì nửa mặt phẳng chứa điểm M (không kể d) là miền nghiệm của bất phương trình ax + by < c.

+) Nếu ax₀ + by₀ > c thì nửa mặt phẳng chứa điểm M (không kể d) là miền nghiệm của bất phương trình ax + by > c.

Ví dụ: Biểu diễn miền nghiệm của bất phương trình x + 3y < 3 và x + 3y ≤ 3.

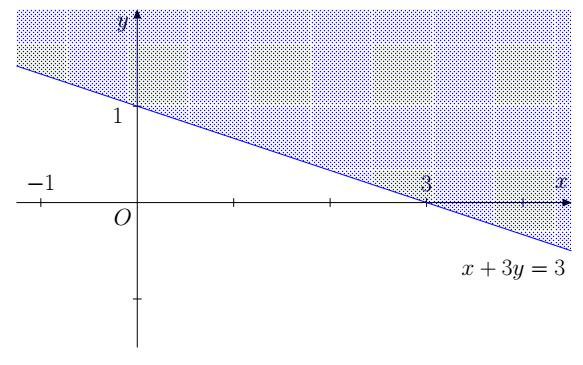
+ Vẽ đường thẳng d: x + 3y = 3

+ Lấy điểm O(0; 0). Ta có: 0 + 3 . 0 = 0 < 3.

+ Vậy:

Miền nghiệm của bất phương trình x + 3y < 3 là nửa mặt phẳng chứa điểm O không kể đường thẳng d.

Miền nghiệm của bất phương trình x + 3y ≤ 3 là nửa mặt phẳng chứa điểm O gồm cả đường thẳng d.

Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

Bài 2: Hệ bất phương trình bậc nhất hai ẩn

Bài tập cuối chương 2

Bài 1: Hàm số và đồ thị

Bài 2: Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng

Bài 3: Dấu của tam thức bậc hai

Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 1: Bất phương trình bậc nhất hai ẩn