Giải Toán 10 Bài 3 (Cánh diều): Khái niệm vectơ

Giải bài tập Toán 10 Bài 3: Khái niệm vectơ

Giải Toán 10 trang 79 Tập 1

Câu hỏi khởi động trang 79 Toán lớp 10 Tập 1: Mũi tên xuất phát từ A đến B trong Hình 34 mô tả chuyển động (có hướng) của một máy bay trên đường băng.

Đoạn thẳng AB có hướng được gọi là gì?

Lời giải:

Đoạn thẳng AB có hướng được gọi là một vectơ.

Hoạt động 1 trang 79 Toán lớp 10 Tập 1: Trong công viên, để chỉ dẫn hướng đi và khoảng cách từ công đến khu vui chơi của trẻ em, người ta vẽ đoạn thẳng có mũi tên như Hình 35. Hình ảnh về mũi tên chỉ dẫn cho ta biết những thông tin gì?

Lời giải:

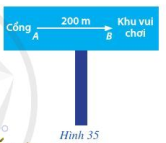
Trên Hình 35, ta có:

- Hướng quy định trên đoạn thẳng AB là hướng xuất phát từ điểm đầu A đến điểm cuối B;

- Đoạn thẳng AB có độ dài bằng 200 m.

Giải Toán 10 trang 80 Tập 1

Luyện tập 1 trang 80 Toán lớp 10 Tập 1: Cho tam giác ABC. Viết tất cả các vectơ mà điểm đầu và điểm cuối là A, B hoặc C.

Lời giải:

Ta có các vectơ thỏa mãn yêu cầu là:

$\overrightarrow{AB};\overrightarrow{AC};\overrightarrow{BA};\overrightarrow{BC};\overrightarrow{CA};\overrightarrow{CB}$.

Hoạt động 2 trang 80 Toán lớp 10 Tập 1: Quan sát Hình 40 và cho biết vị trí tương đối giữa giá của vectơ $\overrightarrow{CD}$ với giá của vectơ $\overrightarrow{AB}$ và $\overrightarrow{PQ}$.

Lời giải:

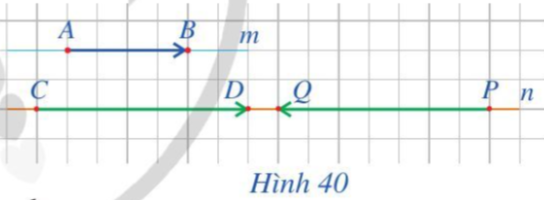
Trong hình trên:

- Giá của vectơ $\overrightarrow{AB}$ là đường thẳng m.

- Giá của vectơ $\overrightarrow{CD}$ là đường thẳng n.

- Giá của vectơ $\overrightarrow{PQ}$ là đường thẳng n.

Do m // n nên giá của vectơ $\overrightarrow{AB}$ song song với giá của vectơ $\overrightarrow{CD}$.

Giá của vectơ $\overrightarrow{PQ}$ trùng với giá của vectơ $\overrightarrow{CD}$.

Hoạt động 3 trang 80 Toán lớp 10 Tập 1: Quan sát hai biển báo ở Hình 41a, Hình 41b, cho biết hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{CD}$ có cùng hướng hay không.

Lời giải:

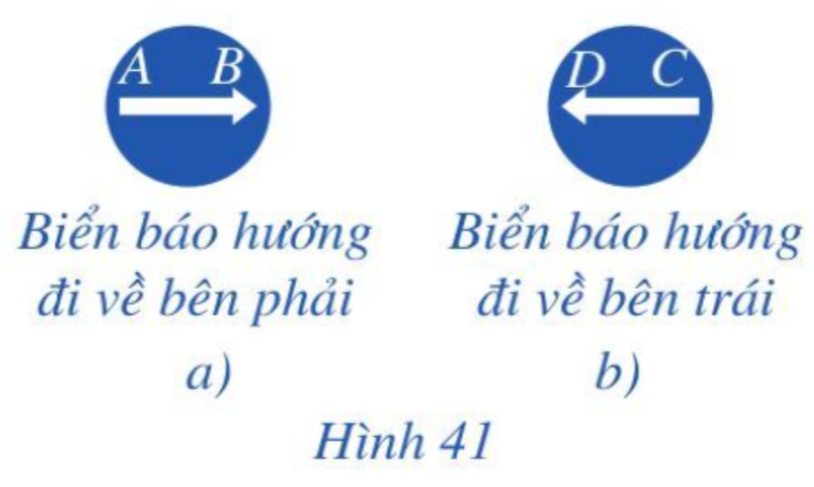
Trong Hình 41, ta thấy

Hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{CD}$ có giá trùng nhau nên hai vecto $\overrightarrow{AB} và \overrightarrow{CD}$ cùng phương

Vecto $\overrightarrow{AB}$hướng đi về bên phải;

Vecto $\overrightarrow{CD}$ hướng đi về bên trái.

Do đó hai vecto cùng phương $\overrightarrow{AB} và \overrightarrow{CD}$ không cùng hướng

Hoạt động 4 trang 80 Toán lớp 10 Tập 1: Quan sát hai vectơ $\overrightarrow{AB},\overrightarrow{CD}$ ở Hình 43.

a) Nhận xét về phương, về hướng của hai vectơ đó.

b) So sánh độ dài của hai vectơ đó.

Lời giải:

a) Quan sát Hình 43, ta thấy:

Vectơ $\overrightarrow{AB}$ có giá là đường thẳng AB;

Vectơ $\overrightarrow{CD}$ có giá là đường thẳng CD;

Mà AB // CD nên hai vectơ $\overrightarrow{AB},\overrightarrow{CD}$ có cùng phương

Ta lại có:

Vectơ $\overrightarrow{AB}$ có hướng từ trái sang phải;

Vectơ $\overrightarrow{CD}$ có hướng từ trái sang phải;

Do đó hai vectơ $\overrightarrow{AB},\overrightarrow{CD}$ cùng hướng.

Vậy hai vectơ $\overrightarrow{AB},\overrightarrow{CD}$ cùng phương và cùng hướng.

b) Quan sát Hình 43, ta thấy:

Vectơ $\overrightarrow{AB}$ có độ dài 5 ô;

Vectơ $\overrightarrow{CD}$ có độ dài 5 ô;

Do đó hai vectơ $\overrightarrow{AB},\overrightarrow{CD}$ có cùng độ dài.

Vậy hai vectơ $\overrightarrow{AB},\overrightarrow{CD}$ có cùng độ dài.

Giải Toán 10 trang 81 Tập 1

Luyện tập 2 trang 81 Toán lớp 10 Tập 1: Cho tam giác ABC. Vẽ điểm D thỏa mãn $\overrightarrow{AD}=\overrightarrow{BC}$. Tứ giác ABCD là hình gì?

Lời giải:

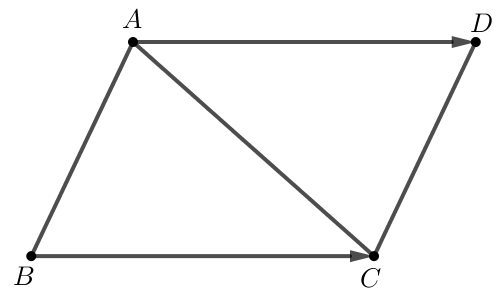
Thực hiện vẽ như sau:

Bước 1. Thực hiện vẽ tam giác ABC bất kì.

Bước 2. Do $\overrightarrow{AD}=\overrightarrow{BC}$ nên vectơ $\overrightarrow{AD}$ cùng phương và cùng hướng với vectơ $\overrightarrow{BC}$.

Do đó D và C cùng nằm ở 1 nửa mặt phẳng có bờ chứa tia AB.

Trên nửa mặt phẳng bờ chứa tia AB chứa điểm C, vẽ đường thẳng d song song với BC.

Bước 3. Trên đường thẳng d chọn điểm D sao cho AD = BC.

Bước 4. Kí hiệu vectơ $\overrightarrow{AD}$ và vectơ $\overrightarrow{BC}$ trên hình ta được $\overrightarrow{AD}=\overrightarrow{BC}$.

Tứ giác ABCD có AD // BC và AD = BC nên tứ giác ABCD là hình bình hành.

Bài tập

Giải Toán 10 trang 82 Tập 1

Bài 1 trang 82 Toán lớp 10 Tập 1: Cho A, B, C là ba điểm thẳng hàng, B nằm giữa A và C. Viết các cặp vectơ cùng hướng, ngược hướng trong những vectơ sau: $\overrightarrow{AB},\overrightarrow{AC},\overrightarrow{BA},\overrightarrow{BC},\overrightarrow{CA},\overrightarrow{CB}$.

Lời giải:

Do B nằm giữa A và C nên B và C cùng nằm ở một phía so với điểm A.

Khi đó các cặp vectơ cùng hướng là:

$\overrightarrow{AB}-\overrightarrow{AC}$; $\overrightarrow{AB}-\overrightarrow{BC}$; $\overrightarrow{AC}-\overrightarrow{BC}$; $\overrightarrow{BA}-\overrightarrow{CA}$; $\overrightarrow{BA}-\overrightarrow{CB}$; $\overrightarrow{CA}-\overrightarrow{CB}$.

Các cặp vectơ ngược hướng là:

$\overrightarrow{AB}-\overrightarrow{BA}$; $\overrightarrow{AB}-\overrightarrow{CA}$; $\overrightarrow{AB}-\overrightarrow{CB}$; $\overrightarrow{AC}-\overrightarrow{BA}$; $\overrightarrow{AC}-\overrightarrow{CB}$; $\overrightarrow{AC}-\overrightarrow{CA}$;

$\overrightarrow{BC}-\overrightarrow{BA}$; $\overrightarrow{BC}-\overrightarrow{CB}$; $\overrightarrow{BC}-\overrightarrow{CA}$.

Bài 2 trang 82 Toán lớp 10 Tập 1: Cho đoạn thẳng MN có trung điểm là I.

a) Viết các vectơ khác vectơ-không có điểm đầu, điểm cuối là một trong ba điểm M, N, I.

b) Vectơ nào bằng $\overrightarrow{MI}$? và $\overrightarrow{NI}$?

Lời giải:

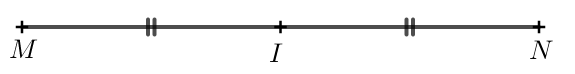
a) Các vectơ khác vectơ-không có điểm đầu, điểm cuối là một trong ba điểm M, N, I là:

$\overrightarrow{MI};\overrightarrow{MN};\overrightarrow{IM};\overrightarrow{IN};\overrightarrow{NM};\overrightarrow{NI}$.

b) Ta thấy I là trung điểm của MN nên MI = NI.

Ta thấy $\overrightarrow{MI}$ và $\overrightarrow{IN}$ là hai vectơ cùng hướng và MI = NI nên $\overrightarrow{MI}=\overrightarrow{IN}$.

$\overrightarrow{NI}$ và $\overrightarrow{IM}$ là hai vectơ cùng hướng và MI = NI nên $\overrightarrow{NI}=\overrightarrow{IM}$.

Vậy $\overrightarrow{MI}=\overrightarrow{IN}$ và $\overrightarrow{NI}=\overrightarrow{IM}$

Bài 3 trang 82 Toán lớp 10 Tập 1: Cho hình thang ABCD có hai đáy là AB và CD. Trong các vectơ khác vectơ-không có điểm đầu, điểm cuối là một trong bốn điểm A, B, C, D, tìm vectơ ngược hướng với vectơ $\overrightarrow{AB}$.

Lời giải:

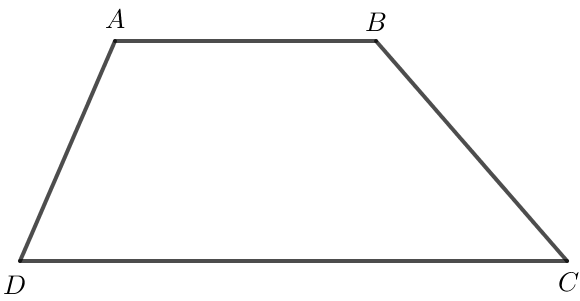
Hình thang ABCD có hai đáy là AB và CD nên AB // CD.

Khi đó vectơ ngược hướng với vectơ $\overrightarrow{AB}$ là vectơ $\overrightarrow{BA}$ và vectơ $\overrightarrow{C\text{D}}$.

Bài 4 trang 82 Toán lớp 10 Tập 1: Cho hình vuông ABCD có độ dài cạnh bằng 3 cm. Tính độ dài của các vectơ $\overrightarrow{AB},\overrightarrow{AC}$.

Lời giải:

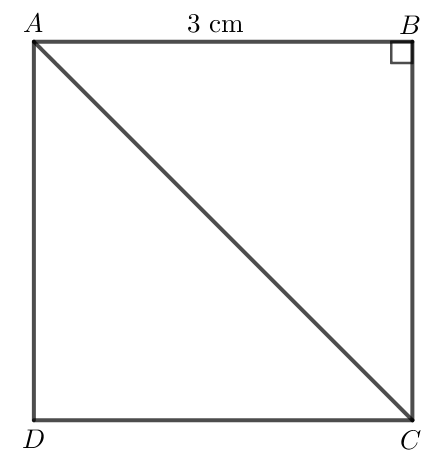
Ta có: $\left|\overrightarrow{AB}\right|$ = AB = 3 cm;

Áp dụng định lí Pythagore vào tam giác ABC vuông tại B ta có:

$\left|\overrightarrow{AC}\right|=AC=\sqrt{A{B}^2+B{C}^2}=\sqrt{3^2+3^2}=3\sqrt{2}$ cm.

Vậy $\left|\overrightarrow{AB}\right|$ = 3 cm; $\left|\overrightarrow{AC}\right|=3\sqrt{2}$ cm.

Bài 5 trang 82 Toán lớp 10 Tập 1: Quan sát ròng rọc hoạt động khi dùng lực để kéo một đầu của ròng rọc. Chuyển động của các đoạn dây được mô tả bằng các vectơ $\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$ (Hình 47).

a) Hãy chỉ ra các cặp vectơ cùng phương.

b) Trong các cặp vectơ đó, cho biết chúng cùng hướng hay ngược hướng.

Lời giải:

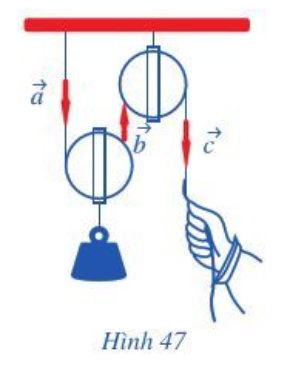
a) Dựa vào Hình 47 ta thấy các cặp vectơ cùng phương là: $\overrightarrow{a}-\overrightarrow{b}$; $\overrightarrow{b}-\overrightarrow{c}$; $\overrightarrow{a}-\overrightarrow{c}$.

b) Quan sát Hình 47 ta thấy:

Cặp vectơ $\overrightarrow{a}-\overrightarrow{b}$ là cặp vectơ ngược hướng.

Cặp vectơ $\overrightarrow{b}-\overrightarrow{c}$ là cặp vectơ ngược hướng.

Cặp vectơ $\overrightarrow{a}-\overrightarrow{c}$ là cặp vectơ cùng hướng.

Lý thuyết Toán 10 Bài 3. Khái niệm vectơ – Cánh diều

1. Khái niệm vectơ

Cho đoạn thẳng AB. Nếu ta chọn điểm A làm điểu đầu, điểm B là điểm cuối thì đoạn thẳng AB có hướng từ A đến B. Khi đó ta nói AB là một đoạn thẳng có hướng.

Định nghĩa: Vectơ là một đoạn thẳng có hướng.

Vectơ có điểm đầu A, điểm cuối B được kí hiệu là $\overrightarrow{\mathrm{AB}}$ và đọc là “vectơ AB”. Để vẽ được vectơ $\overrightarrow{\mathrm{AB}}$ ta vẽ đoạn thẳng AB và đánh dấu mũi tên ở đầu nút B.

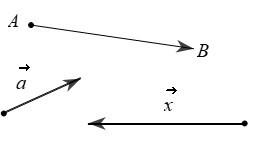
Đối với vectơ $\overrightarrow{\mathrm{AB}}$, ta gọi:

– Đường thẳng d đi qua hai điểm A và B là giá của vectơ $\overrightarrow{\mathrm{AB}}$.

– Độ dài đoạn thẳng AB là độ dài của vectơ $\overrightarrow{\mathrm{AB}}$, kí hiệu là $\left|\overrightarrow{\mathrm{AB}}\right|$.

Vectơ còn được kí hiệu là $\overrightarrow{\mathrm{a}}$, $\overrightarrow{\mathrm{b}}$, $\overrightarrow{\mathrm{x}}$, $\overrightarrow{\mathrm{y}}$ khi không cần chỉ rõ điểm đầu và điểm cuối của nó. Độ dài của vectơ $\overrightarrow{\mathrm{a}}$ được kí hiệu là $\left|\overrightarrow{\mathrm{a}}\right|.$

Ví dụ: Vectơ $\overrightarrow{\mathrm{AB}}$ có độ dài là 5, ta có thể viết như sau: $\left|\overrightarrow{\mathrm{AB}}\right|$ = 5.

2. Vectơ cùng phương, vectơ cùng hướng

Định nghĩa:

– Hai vectơ cùng phương: Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

Ví dụ:

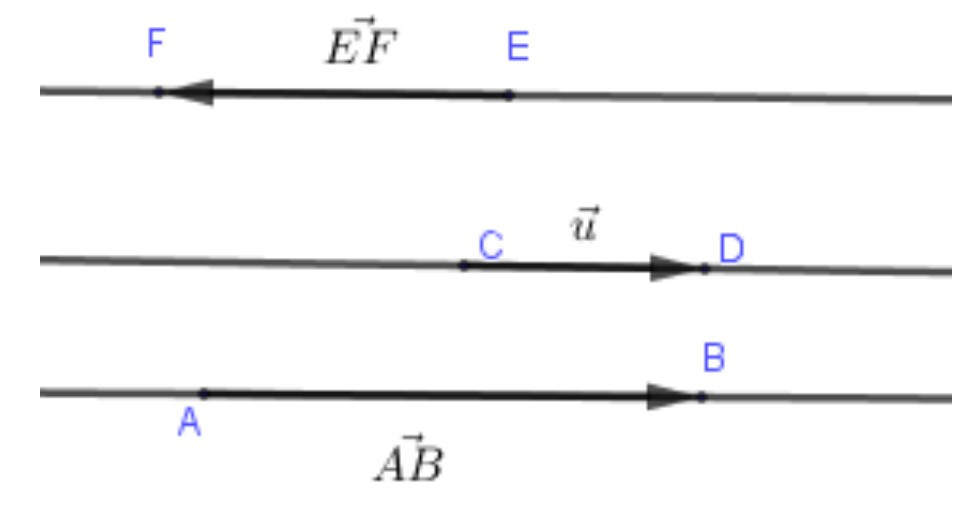
Trên hình vẽ các vectơ $\overrightarrow{\mathrm{AB}}$, $\overrightarrow{\mathrm{CD}}$, $\stackrel{\rightharpoonup }{\mathrm{EF}}$ cùng phương với nhau.

Nhận xét: Hai vectơ cùng phương có thể cùng hướng hoặc ngược hướng.

Ví dụ:

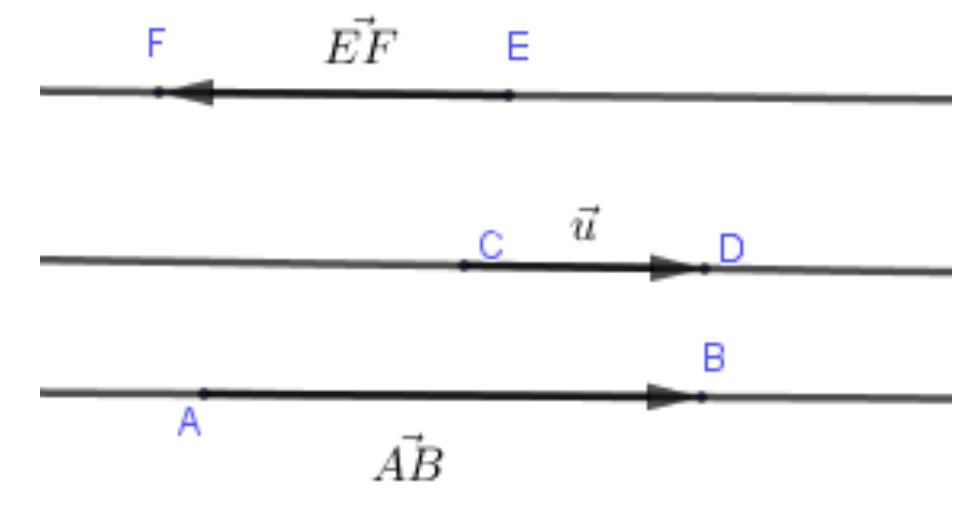
Hai vectơ $\overrightarrow{\mathrm{AB}}$ và $\overrightarrow{\mathrm{CD}}$cùng phương và có cùng hướng đi từ trái sang phải. Ta nói hai vectơ $\overrightarrow{\mathrm{AB}}$ và $\overrightarrow{\mathrm{CD}}$ cùng hướng. Hai vectơ $\overrightarrow{\mathrm{CD}}$ và $\stackrel{\rightharpoonup }{\mathrm{EF}}$cùng phương nhưng ngược hướng nhau. Ta nói hai vectơ $\overrightarrow{\mathrm{CD}}$ và $\stackrel{\rightharpoonup }{\mathrm{EF}}$ là hai vectơ ngược hướng.

Ví dụ: Cho hình bình hành ABCD. Liệt kê các cặp vectơ cùng hướng và ngược hướng trong hình bình hành ABCD.

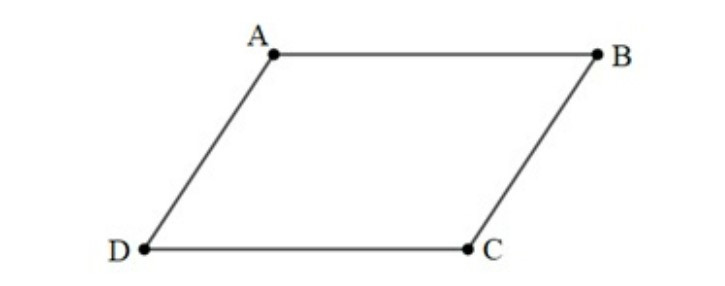
Hướng dẫn giải:

Do ABCD là hình bình hành nên ta có: AB // DC và AD // BC.

Các cặp vectơ cùng hướng: $\overrightarrow{\mathrm{AB}}$và $\overrightarrow{\mathrm{DC}}$, $\overrightarrow{\mathrm{AD}}$và $\overrightarrow{\mathrm{BC}}$, $\overrightarrow{\mathrm{BA}}$và $\overrightarrow{\mathrm{CD}}$, $\overrightarrow{\mathrm{DA}}$ và $\overrightarrow{\mathrm{CB}}$.

Các cặp vectơ ngược hướng: $\overrightarrow{\mathrm{AB}}$và $\overrightarrow{\mathrm{CD}}$, $\overrightarrow{\mathrm{AD}}$và $\overrightarrow{\mathrm{CB}}$, $\overrightarrow{\mathrm{BA}}$và $\overrightarrow{\mathrm{DC}}$, $\overrightarrow{\mathrm{DA}}$và $\overrightarrow{\mathrm{BC}}$.

3. Hai vectơ bằng nhau

Hai vectơ $\overrightarrow{\mathrm{AB}}$, $\overrightarrow{\mathrm{CD}}$ bằng nhau nếu chúng cùng hướng và cùng độ dài, kí hiệu: $\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{CD}}.$

Nhận xét:

– Hai vectơ $\overrightarrow{\mathrm{a}}$ và $\overrightarrow{\mathrm{b}}$ được gọi là bằng nhau nếu chúng cùng hướng và có cùng độ dài, kí hiệu $\overrightarrow{\mathrm{a}}$ = $\overrightarrow{\mathrm{b}}$.

– Khi cho trước vectơ $\overrightarrow{\mathrm{a}}$ và điểm O, thì ta luôn tìm được một điểm A duy nhất sao cho $\overrightarrow{\mathrm{OA}}=\overrightarrow{\mathrm{a}}.$

Ví dụ: Cho hình bình hành ABCD, khi đó:

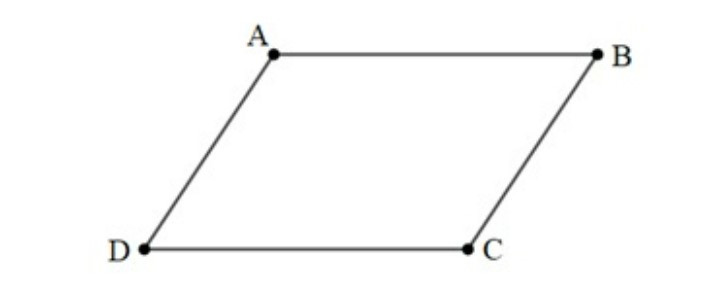
Do ABCD là hình bình hành nên ta có:

$\left\{\begin{array}{l}\mathrm{AB}//\mathrm{DC}\mathrm{và}\mathrm{AD}//\mathrm{BC}\\ \mathrm{AB}=\mathrm{CD}\mathrm{và}\mathrm{AD}=\mathrm{BC}\end{array}\right.$

Ta lại có: $\overrightarrow{\mathrm{AB}}$và $\overrightarrow{\mathrm{DC}}$ ; $\overrightarrow{\mathrm{AD}}$ và $\overrightarrow{\mathrm{BC}}$ là hai cặp vectơ cùng hướng nên $\left\{\begin{array}{l}\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{DC}}\\ \overrightarrow{\mathrm{AD}}=\overrightarrow{\mathrm{BC}}\end{array}\right.$.

4. Vectơ–không

Ta biết rằng mỗi vectơ có một điểm đầu và một điểm cuối và hoàn toàn được xác định khi biết điểm đầu và điểm cuối của nó.

Bây giờ với một điểm A bất kì ta quy ước có một vectơ đặc biệt mà điểm đầu và điểm cuối đều là A. Vectơ này được kí hiệu là $\overrightarrow{\mathrm{AA}}$ và được gọi là vectơ – không.

Định nghĩa: Vectơ–không là vectơ có điểm đầu và điểm cuối trùng nhau, kí hiệu là $\overrightarrow{0}.$

Ta quy ước $\overrightarrow{0}.$ cùng phương và cùng hướng với mọi vectơ và $\left|\overrightarrow{0}\right|$ = 0.

Nhận xét: Hai điểm A, B trùng nhau khi và chỉ khi $\overrightarrow{\mathrm{AB}}$= $\overrightarrow{0}$.

Ví dụ: Vectơ $\overrightarrow{\mathrm{BB}}$ là vectơ – không và $\left|\overrightarrow{\mathrm{BB}}\right|=0.$

5. Biểu thị một số đại lượng có hướng bằng vectơ

Trong vật lý, một số đại lượng như trọng lực, vận tốc,… là đại lượng có hướng. Người ta dùng vectơ để biểu thị các đại lượng đó.

Ví dụ: Chọn trục tọa độ là trục Oy có chiều hướng lên trên, biểu điễn vectơ lực $\overrightarrow{\mathrm{F}}$ có điểm đặt tại gốc O trong hai trường hợp sau:

a) $\overrightarrow{\mathrm{F}}$ có phương thẳng đứng chiều hướng xuống

b) $\overrightarrow{\mathrm{F}}$ có phương thẳng đứng hướng lên trên

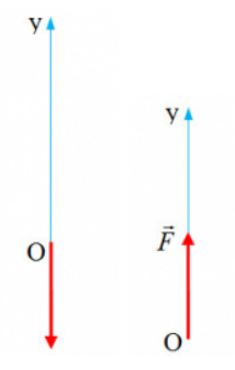
Ta thấy vectơ lực $\overrightarrow{\mathrm{F}}$ ở hai trường hợp cùng phương nhưng ngược hướng với nhau.