Cho tam giác ABC và các điểm M, N, P đôi một phân biệt thoả mãn MA = MB = MC, NA = NB
Lời giải Bài 17 trang 95 SBT Toán 11 Tập 2 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11.
Giải SBT Toán 11 Bài 2: Đường thẳng vuông góc với mặt phẳng
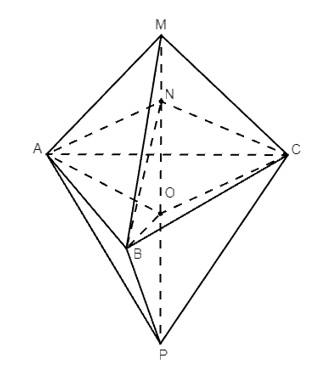
Bài 17 trang 95 SBT Toán 11 Tập 2: Cho tam giác ABC và các điểm M, N, P đôi một phân biệt thoả mãn MA = MB = MC, NA = NB = NC, PA = PB = PC. Chứng minh rằng M, N, P thẳng hàng.
Lời giải:
Gọi O là tâm đường tròn ngoại tiếp của tam giác ABC.
Khi đó OA = OB = OC.
⦁ Trường hợp 1: Ba điểm M, N, P đều không thuộc mặt phẳng (ABC).
Xét hình chóp M.ABC có MA = MB = MC nên theo kết quả của Bài 16, trang 95, Sách bài tập Toán 11, Tập hai ta có: MO ⊥ (ABC)
Tương tự, từ NA = NB = NC, PA = PB = PC ta cũng có NO ⊥ (ABC), PO ⊥ (ABC).
Ta thấy: MO, NO, PO cùng đi qua điểm O và vuông góc với mặt phẳng (ABC).
Do đó ba đường thẳng MO, NO, PO trùng nhau hay M, N, P thẳng hàng.
⦁ Trường hợp 2: Trong ba điểm M, N, P có một điểm nằm trên (ABC).
Mà MA = MB = MC, NA = NB = NC, PA = PB = PC nên không mất tính tổng quát ta giả sử điểm M nằm trên (ABC).
Ta có MA = MB = MC, OA = OB = OC và M, O cùng nằm trong mp (ABC)
Suy ra: M ≡ O.
Tương tự trường hợp 1, từ NA = NB = NC, PA = PB = PC nên cũng ta có:
NO ⊥ (ABC), PO ⊥ (ABC).
Ta thấy: NO, PO cùng đi qua điểm O và vuông góc với mặt phẳng (ABC).
Do đó hai đường thẳng NO, PO trùng nhau hay O, N, P thẳng hàng hay M, N, P thẳng hàng.
Vậy M, N, P thẳng hàng.
Xem thêm lời giải SBT Toán lớp 11 bộ sách Cánh diều hay, chi tiết khác:
Bài 12 trang 94 SBT Toán 11 Tập 2: Cho hình chóp S.ABC có ...
Bài 18 trang 95 SBT Toán 11 Tập 2: Cho hình tứ diện đều ABCD. Chứng minh AB ⊥ CD.....
Bài 19 trang 95 SBT Toán 11 Tập 2: Cho hình tứ diện ABCD có AB ⊥ (BCD), các tam giác BCD và ACD...
Bài 21 trang 95 SBT Toán 11 Tập 2: Cho hình chóp S.ABCD thoả mãn SA = SB = SC = SD...
Bài 22 trang 95 SBT Toán 11 Tập 2: Cho mặt phẳng (P) và hai điểm A, B sao cho B thuộc (P) và A...
Xem thêm lời giải SBT Toán lớp 11 bộ sách Cánh diều hay, chi tiết khác:
Bài 3: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
Bài 4: Hai mặt phẳng vuông góc
Bài 6: Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Cánh diều (hay nhất)
- Văn mẫu lớp 11 - Cánh diều
- Tóm tắt tác phẩm Ngữ văn 11 – Cánh diều
- Tác giả tác phẩm Ngữ văn 11 - Cánh diều
- Giải SBT Ngữ văn 11 – Cánh diều
- Bố cục tác phẩm Ngữ văn 11 – Cánh diều
- Giải Chuyên đề học tập Ngữ văn 11 – Cánh diều
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Cánh diều
- Soạn văn 11 Cánh diều (ngắn nhất)
- Giải sgk Tiếng Anh 11 – ilearn Smart World
- Giải sbt Tiếng Anh 11 - ilearn Smart World
- Trọn bộ Từ vựng Tiếng Anh 11 ilearn Smart World đầy đủ nhất
- Giải sgk Vật lí 11 – Cánh diều
- Lý thuyết Vật lí 11 – Cánh diều
- Giải sbt Vật lí 11 – Cánh diều
- Giải Chuyên đề học tập Vật lí 11 – Cánh diều
- Giải sgk Hóa học 11 – Cánh diều
- Giải Chuyên đề học tập Hóa học 11 – Cánh diều
- Lý thuyết Hóa 11 - Cánh diều
- Giải sbt Hóa học 11 – Cánh diều
- Giải sgk Sinh học 11 – Cánh diều
- Lý thuyết Sinh học 11 – Cánh diều
- Giải Chuyên đề học tập Sinh học 11 – Cánh diều
- Giải sbt Sinh học 11 – Cánh diều
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Cánh diều
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Cánh diều
- Lý thuyết Kinh tế pháp luật 11 – Cánh diều
- Giải sbt Kinh tế pháp luật 11 – Cánh diều
- Giải sgk Lịch sử 11 – Cánh diều
- Giải Chuyên đề học tập Lịch sử 11 – Cánh diều
- Lý thuyết Lịch sử 11 - Cánh diều
- Giải sbt Lịch sử 11 – Cánh diều
- Giải sgk Địa lí 11 – Cánh diều
- Giải Chuyên đề học tập Địa lí 11 – Cánh diều
- Lý thuyết Địa lí 11 - Cánh diều
- Giải sbt Địa lí 11 – Cánh diều
- Giải sgk Công nghệ 11 – Cánh diều
- Lý thuyết Công nghệ 11 - Cánh diều
- Giải sbt Công nghệ 11 – Cánh diều
- Giải sgk Tin học 11 – Cánh diều
- Giải Chuyên đề học tập Tin học 11 – Cánh diều
- Lý thuyết Tin học 11 - Cánh diều
- Giải sbt Tin học 11 – Cánh diều
- Giải sgk Giáo dục quốc phòng an ninh 11 – Cánh diều
- Lý thuyết Giáo dục quốc phòng 11 – Cánh diều
- Giải sbt Giáo dục quốc phòng 11 – Cánh diều
- Giải sgk Hoạt động trải nghiệm 11 – Cánh diều