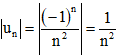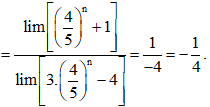Sách bài tập Toán 11 Bài 1 (Cánh diều): Giới hạn của dãy số
Với giải sách bài tập Toán 11 Bài 1: Giới hạn của dãy số sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 11 Bài 1.
Giải SBT Toán 11 Bài 1: Giới hạn của dãy số
Bài 1 trang 68 SBT Toán 11 Tập 1: Phát biểu nào sau đây là sai?
Lời giải:
Đáp án đúng là: B
Vì limqn = 0 với |q| < 1 nên ta có:
lim12n=lim(12)n=0 do 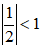
lim1(√2)n=lim(1√2)n=0 do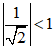
lim(−√32)n=0 do 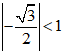
Vậy các đáp án A, C, D đúng.
Vì 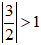
Bài 2 trang 68 SBT Toán 11 Tập 1: Cho limun = a, lim vn = b. Phát biểu nào sau đây là sai?
Lời giải:
Đáp án đúng là: D
Theo định lí về giới hạn hữu hạn thì ta thấy đáp án D sai.
Bài 3 trang 68 SBT Toán 11 Tập 1: Nếu limun = C và limvn = +∞ (hoặc limvn = −∞) thì limunvn bằng:
Lời giải:
Đáp án đúng là: A
Nếu limun = C và limvn = +∞ (hoặc limvn = −∞) thì limunvn=0 .
Bài 4 trang 68 SBT Toán 11 Tập 1: Phát biểu nào sau đây là sai?
A. Nếu limun = +∞ và limvn = C, C > 0 thì lim unvn = +∞.
B. Nếu limun = −∞ và limvn = C, C < 0 thì lim unvn = +∞.
C. Nếu limun = +∞ và limvn = C, C < 0 thì lim unvn= 0.
D. Nếu limun = –∞ và limvn = C, C > 0 thì limunvn=−∞ .
Lời giải:
Đáp án đúng là: C
Theo định lí giữa giới hạn hữu hạn và giới hạn vô cực, nếu limun = +∞ và limvn = C, C < 0 thì limunvn = –∞ nên đáp án C sai.
Bài 5 trang 68 SBT Toán 11 Tập 1: Phát biểu nào sau đây là đúng?
A. Nếu limun = a thì lim√un=√a .
B. Nếu limun = a thì a ≥ 0 và lim√un=√a .
D. Nếu un ≥ 0 với mọi n và limun = a thì a ≥ 0 và lim√un=√a .
Lời giải:
Đáp án đúng là: D
Theo định lí về giới hạn hữu hạn, nếu un ≥ 0 với mọi n và limun = a thì a ≥ 0 và lim√un=√a .
Bài 6 trang 68 SBT Toán 11 Tập 1: Chứng minh rằng lim(−1)nn2=0 .
Lời giải:
Xét dãy số (un) có un=(−1)nn2.
Giả sử h là số dương bé tùy ý cho trước. Ta có:
Do đó, 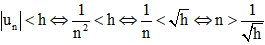
Vậy với các số tự nhiên n lớn hơn 1√h thì |un| < h.
Suy ra lim(−1)nn2=0 .
Bài 7 trang 68 SBT Toán 11 Tập 1: Cho hai dãy số (un), (vn) với un=3−4n+1 , vn=8−53n2+2 . Tính:
b) lim(un + vn), lim(un – vn), lim(un . vn), limunvn .
Lời giải:
a) Ta có
limun=lim(3−4n+1)=lim3−lim4n+1=3−0=3;
limvn=lim(8−53n2+2)=lim8−lim53n2+2=8−0=8.
b) Ta có
lim(un + vn) = limun + limvn = 3 + 8 = 11;
lim(un – vn) = limun – limvn = 3 – 8 = – 5;
lim(un . vn) = limun . limvn = 3 . 8 = 24;
limunvn=limunlimvn=38.
Bài 8 trang 68 SBT Toán 11 Tập 1: Tính các giới hạn sau:
Lời giải:
a) Vì lim(4n + 2) =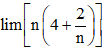
Do đó, lim4n+23=+∞.
b) Vì lim(3n + 4) 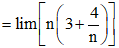
và lim(−5+2n)=lim(−5)+lim2n=−5 < 0.
Do đó, lim3n+4−5+2n=−∞ .
c) Vì lim(−3+1n+1)=lim(−3)+lim1n+1=−3 và lim5n = +∞.
Nên lim−3+1n+15n=0 .
d) lim(6−54n)=lim6−lim54n=6−lim(5.14n)
=6−5lim(14)n=6−5.0=6.
Bài 9 trang 69 SBT Toán 11 Tập 1: Tính các giới hạn sau:
Lời giải:
a) lim6n−53n=limn(6−5n)3n=lim6−5n3=lim(6−5n)lim3=63=2 .
b) lim−2n2−6n+28n2−5n+4 =limn2(−2−6n+2n2)n2(8−5n+4n2)
=lim−2−6n+2n28−5n+4n2=lim(−2−6n+2n2)lim(8−5n+4n2)=−28=−14.
c) limn3−5n+13n2−4n+2=limn3(1−5n2+1n3)n3(3n−4n2+2n3)=lim1−5n2+1n33n−4n2+2n3
=lim(1−5n2+1n3)lim(3n−4n2+2n3)=+∞ (do lim(1−5n2+1n3)=1 và lim(3n−4n2+2n3)=0 ).
d) lim−4n+19n2−n+2=limn2(−4n+1n2)n2(9−1n+2n2) =lim−4n+1n29−1n+2n2
=lim(−4n+1n2)lim(9−1n+2n2)=09=0 .
e) lim√4n2+n+18n+3 =lim√n2(4+1n+1n2)n(8+3n) =lim√4+1n+1n28+3n
=lim(√4+1n+1n2)lim(8+3n)=√lim(4+1n+1n2)lim(8+3n)=√48=28=14.
g) lim4n+5n3.4n−4.5n=lim5n(4n5n+1)5n(3.4n5n−4)=lim(45)n+13.(45)n−4
Bài 10 trang 69 SBT Toán 11 Tập 1: a) Tính tổng của cấp số nhân lùi vô hạn (un) với u1=54,q=−13 .
b) Biểu diễn số thập phân vô hạn tuần hoàn 2,(3) dưới dạng phân số.
Lời giải:
a) Tổng của cấp số nhân lùi vô hạn (un) với u1=54,q=−13 là:
S=u11−q=541−(−13)=1516.
b) Ta có 2,(3) = 2 + 0,(3) = 2 + 0,3 + 0,03 + 0,003 + ... + 0,0000003 + ...
Dãy số 0,3; 0,03; 0,003; ...lập thành một cấp số nhân lùi vô hạn có số hạng đầu u1 = 0,3 và công bội q=110 < 1. Do đó:
0,3 + 0,03 + 0,003 + ... + 0,0000003 + ... =0,31−110=13 .
Vậy 2,(3) = 2 + 13=73 .
a) Tìm số hạng tổng quát của dãy số (hn).
b) Tính giới hạn của dãy số (hn) và nêu ý nghĩa giới hạn của dãy số (hn).
Lời giải:
a) Theo đề bài ta có, hn=14hn−1 nên (hn) là một cấp số nhân với h1 = 14.100=25 và công bội q=14 .
Suy ra số hạng tổng quát của dãy số (hn): hn=u1qn−1=25.(14)n−1=1004n .
b) Ta có: limhn = lim1004n=lim(100.14n)=lim100.lim(14)n=100.0=0 .
Từ giới hạn đó, ta rút ra được ý nghĩa: Khi n càng dần tới vô cực thì độ cao của quả bóng đạt được sau khi nảy ngày càng nhỏ và độ cao đó dần tới 0.
c) Ta có: Sn=100+2(1004+10042+10043+...+1004n) .
Nếu quá trình bóng nảy cứ tiếp tục diễn ra mãi, tổng quãng đường quả bóng di chuyển được là: limSn=100+2(1004+10042+10043+...+1004n+...) .
Vì 1004; 10042; 10043;...;1004n;... lập thành một cấp số nhân lùi vô hạn với u1=1004 và công bội q=14<1 nên ta có limSn=100+2.10041−14=5003 .
Vậy tổng quãng đường quả bóng di chuyển được là 5003 m.
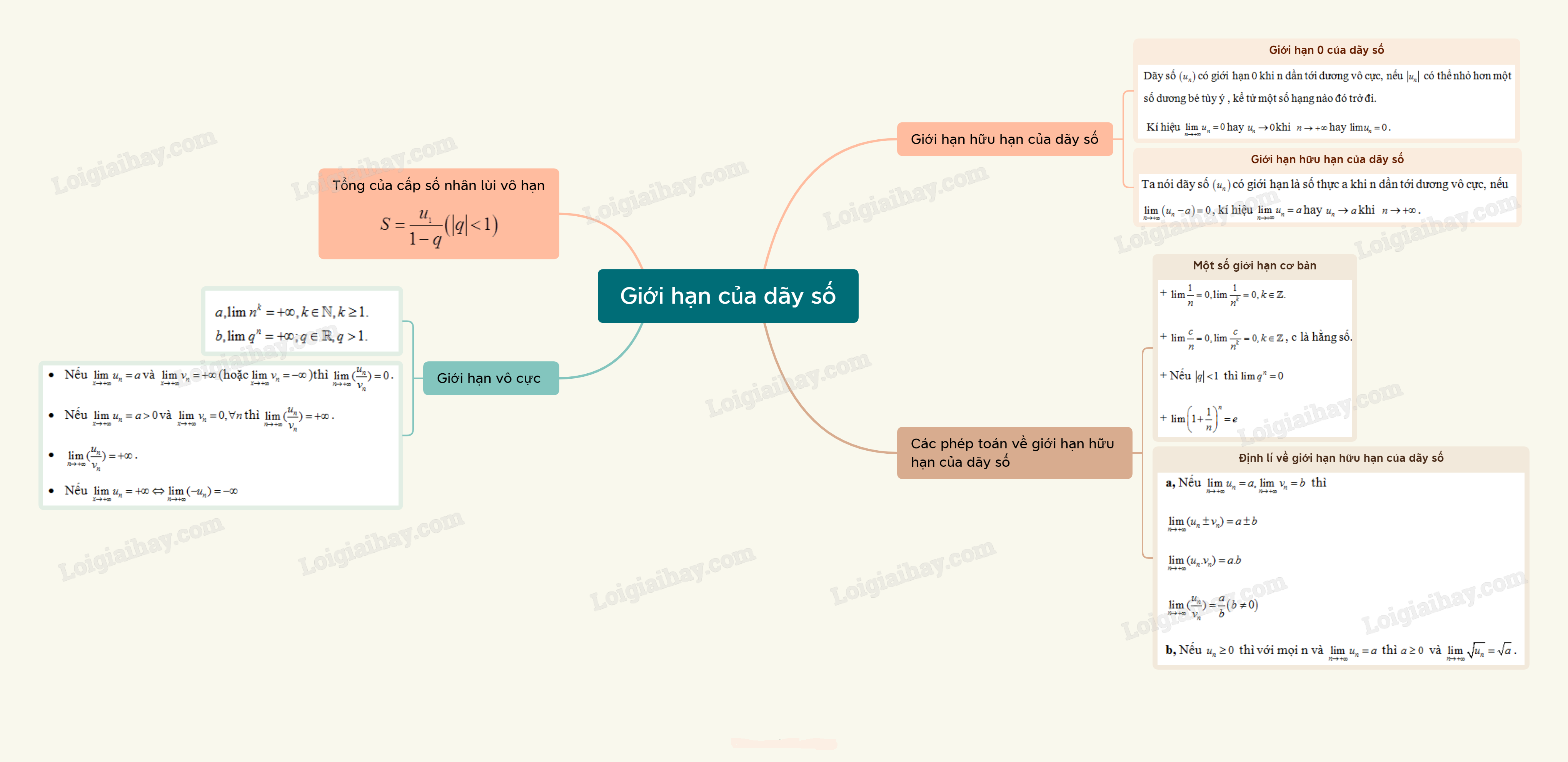
Lý thuyết Giới hạn của dãy số
1. Giới hạn hữu hạn của dãy số
- Dãy số (un) có giới hạn 0 khi n dần tới dương vô cực, nếu |un| có thể nhỏ hơn một số dương bé tùy ý , kể tử một số hạng nào đó trở đi.
Kí hiệu hay khi hay .
- Dãy số có giới hạn là số thực a khi n dần tới dương vô cực, nếu , kí hiệu hay khi hay .
* Chú ý: Nếu (c là hằng số) thì
2. Một số giới hạn cơ bản
+
+ , c là hằng số.
+ Nếu thì
+
3. Định lí về giới hạn hữu hạn của dãy số
a, Nếu thì
b, Nếu thì với mọi n và thì và .
3. Tổng của cấp số nhân lùi vô hạn
Cấp số nhân lùi vô hạn có công bội q thỏa mãn được gọi là cấp số nhân lùi vô hạn.
Tổng của cấp số nhân lùi vô hạn là:
4. Giới hạn vô cực
- Dãy số được gọi là có giới hạn khi nếu có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi, kí hiệu hay khi .
- Dãy số được gọi là có giới hạn khi nếu , kí hiệu hay khi .
*Nhận xét:
- Nếu và (hoặc) thì .
- Nếu và thì .
- .
- Nếu
Xem thêm Lời giải bài tập SBT Toán 11 sách Cánh diều hay, chi tiết khác:
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Cánh diều (hay nhất)
- Văn mẫu lớp 11 - Cánh diều
- Tóm tắt tác phẩm Ngữ văn 11 – Cánh diều
- Tác giả tác phẩm Ngữ văn 11 - Cánh diều
- Giải SBT Ngữ văn 11 – Cánh diều
- Bố cục tác phẩm Ngữ văn 11 – Cánh diều
- Giải Chuyên đề học tập Ngữ văn 11 – Cánh diều
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Cánh diều
- Soạn văn 11 Cánh diều (ngắn nhất)
- Giải sgk Tiếng Anh 11 – ilearn Smart World
- Giải sbt Tiếng Anh 11 - ilearn Smart World
- Trọn bộ Từ vựng Tiếng Anh 11 ilearn Smart World đầy đủ nhất
- Giải sgk Vật lí 11 – Cánh diều
- Lý thuyết Vật lí 11 – Cánh diều
- Giải sbt Vật lí 11 – Cánh diều
- Giải Chuyên đề học tập Vật lí 11 – Cánh diều
- Giải sgk Hóa học 11 – Cánh diều
- Giải Chuyên đề học tập Hóa học 11 – Cánh diều
- Lý thuyết Hóa 11 - Cánh diều
- Giải sbt Hóa học 11 – Cánh diều
- Giải sgk Sinh học 11 – Cánh diều
- Lý thuyết Sinh học 11 – Cánh diều
- Giải Chuyên đề học tập Sinh học 11 – Cánh diều
- Giải sbt Sinh học 11 – Cánh diều
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Cánh diều
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Cánh diều
- Lý thuyết Kinh tế pháp luật 11 – Cánh diều
- Giải sbt Kinh tế pháp luật 11 – Cánh diều
- Giải sgk Lịch sử 11 – Cánh diều
- Giải Chuyên đề học tập Lịch sử 11 – Cánh diều
- Lý thuyết Lịch sử 11 - Cánh diều
- Giải sbt Lịch sử 11 – Cánh diều
- Giải sgk Địa lí 11 – Cánh diều
- Giải Chuyên đề học tập Địa lí 11 – Cánh diều
- Lý thuyết Địa lí 11 - Cánh diều
- Giải sbt Địa lí 11 – Cánh diều
- Giải sgk Công nghệ 11 – Cánh diều
- Lý thuyết Công nghệ 11 - Cánh diều
- Giải sbt Công nghệ 11 – Cánh diều
- Giải sgk Tin học 11 – Cánh diều
- Giải Chuyên đề học tập Tin học 11 – Cánh diều
- Lý thuyết Tin học 11 - Cánh diều
- Giải sbt Tin học 11 – Cánh diều
- Giải sgk Giáo dục quốc phòng an ninh 11 – Cánh diều
- Lý thuyết Giáo dục quốc phòng 11 – Cánh diều
- Giải sbt Giáo dục quốc phòng 11 – Cánh diều
- Giải sgk Hoạt động trải nghiệm 11 – Cánh diều