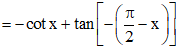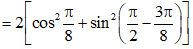Sách bài tập Toán 11 Bài 1 (Cánh diều): Góc lượng giác. Giá trị lượng giác của góc lượng giác
Với giải sách bài tập Toán 11 Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 11 Bài 1.
Giải SBT Toán 11 Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác
Lời giải:
Đáp án đúng là: C
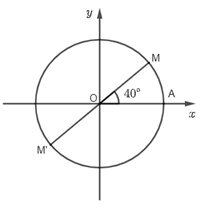
Vì M, M' đối xứng nhau qua gốc tọa độ O nên M, O, M' thẳng hàng.
Ta có:
(OA, OM') = (OA, OM) + (OM, OM') + k360°
= 40° + 180° + k360° = 220° + k360°.
Bài 2 trang 10 SBT Toán 11 Tập 1: Cho với . Khi đó, tan α bằng:
Lời giải:
Đáp án đúng là: B
Vì nên tan α < 0.
Do đó, từ , ta suy ra
.
Bài 3 trang 10 SBT Toán 11 Tập 1: Cho tan α + cot α = 2. Khi đó, tan2 α + cot2 α bằng:
Lời giải:
Đáp án đúng là: D
Ta có tan α + cot α = 2
Suy ra (tan α + cot α)2 = 22 = 4.
Mà (tan α + cot α)2 = tan2 α + 2tan α . cot α + cot2 α
= tan2 α + 2 . 1 + cot2 α = tan2 α + cot2 α + 2 = 4.
Do đó, tan2 α + cot2 α = 4 – 2 = 2.
Bài 4 trang 10 SBT Toán 11 Tập 1: Kết quả thu gọn của biểu thức
Lời giải:
Đáp án đúng là: A
Bài 5 trang 10 SBT Toán 11 Tập 1: Cho tan α = 2. Khi đó giá trị của biểu thức bằng:
Lời giải:
Đáp án đúng là: B
Vì tan α = 2 xác định nên cos α ≠ 0, hay cos2 α ≠ 0, do đó chia cả tử và mẫu của A cho cos2 α ta được:
.
Lời giải:
Vì ABCDEF là lục giác đều nên
.
Khi đó, ta có:
;
;
;
;
.
Bài 7 trang 11 SBT Toán 11 Tập 1: Cho với . Tính cos α, tanα, cot α.
Lời giải:
Vì nên cos α < 0.
Do đó từ sin2 α + cos2 α = 1, suy ra
.
Khi đó, ;
.
Bài 8 trang 11 SBT Toán 11 Tập 1: Cho cot x = – 3, . Tính sin x, cos x, tan x.
Lời giải:
Ta có: .
Áp dụng công thức , ta được .
Mà nên sin x > 0. Suy ra .
Khi đó từ , suy ra cos x = cot x . sin x = .
Bài 9 trang 11 SBT Toán 11 Tập 1: Chứng minh rằng:
a) sin4 x + cos4 x = 1 − 2sin2 x cos2 x;
b) sin6 x + cos6 x = 1 – 3sin2 x cos2 x.
Lời giải:
a) VT = sin4 x + cos4 x
= (sin2 x)2 + (cos2 x)2 + 2sin2 x . cos2 x – 2sin2 x . cos2 x
= (sin2 x + cos2 x)2 – 2sin2 x . cos2 x
= 12 – 2sin2 x . cos2 x = 1 – 2sin2 x . cos2 x = VP (đpcm).
b) VT = sin6 x + cos6 x
= (sin2 x)3 + (cos2 x)3
= (sin2 x + cos2 x)3 – 3sin2 x cos2 x(sin2 x + cos2 x)
= 13 – 3sin2 x cos2 x . 1
= 1 – 3sin2 x cos2 x (đpcm).
Bài 10 trang 11 SBT Toán 11 Tập 1: Cho tan x = − 2. Tính giá trị của mỗi biểu thức sau:
Lời giải:
a) Vì tan x xác định nên cos x ≠ 0. Chia cả tử và mẫu của A cho cos x ta được:
.
b) Vì tan x xác định nên cos2 x khác 0. Chia cả tử và mẫu của B cho cos2 x ta được:
.
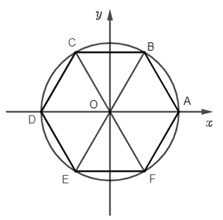
Bài 11 trang 11 SBT Toán 11 Tập 1: Tính:
c) C = tan 1° . tan 2° . tan 3°. ... . tan 89° (gồm 89 thừa số).
Lời giải:
a) Do ;
.
Nên A =
=
.
b) Nhận thấy nên .
Tương tự ta có: .
Suy ra B =
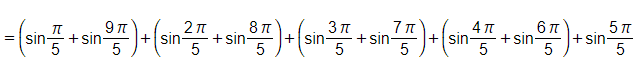
.
c) C = tan 1° . tan 2° . tan 3°. ... . tan 89°
= (tan 1° . tan 89°) . (tan 2° . tan 88°) . ... . (tan 44° . tan 46°) . tan 45°
= [tan 1° . cot(90° – 89°)] . [tan 2° . cot(90° – 88°)] . ... . [tan44° . cot(90° – 46°)] . tan 45°
= (tan 1° . cot 1°) . (tan 2° . cot 2°) . ... . (tan 44° . cot 44°) . tan 45°
= 1 . 1 . ... . 1 . 1
= 1.
Bài 12 trang 11 SBT Toán 11 Tập 1: Chứng minh rằng trong tam giác ABC, ta có:
Lời giải:
Sử dụng định lí tổng 3 góc trong tam giác.
a) Do A + C = π – B nên sin(A + C) = sin(π – B) = sin B.
Vậy sin B = sin(A + C).
b) Do A + B + 2C = A + B + C + C = π + C
Nên cos(A + B + 2C) = cos(π + C) = – cos C.
Suy ra cosC = – cos(A + B + 2C).
c) Ta có: , suy ra .
Nên .
d) Ta có: .
Suy ra .
Bài 13 trang 11 SBT Toán 11 Tập 1: Cho sin α + cos α = với . Tính:
Lời giải:
a) Do sin α + cos α = nên (sin α + cos α)2 = .
Mà (sin α + cos α)2 = sin2 α + 2 sin α cos α + cos2 α = 1 + 2 sin α cos α.
Do đó, 1 + 2 sin α cos α = , suy ra A = sinα . cos α = .
b) Ta có: B2 = (sin α – cos α)2 = 1 – 2 sin α cos α = .
Do nên sin α < 0 và cos α > 0. Do đó sin α – cos α < 0.
Vậy B = .
c) Ta có:
C = sin³ α + cos³ α = (sin α + cos α)3 – 3 sin α cos α(sin α + cos α)
.
d) Ta có:
D = sin4 α + cos4 α = 1 – 2sin2 α cos2 α (theo Bài 9a)
= 1 – 2 (sin α cos α)2 = .
Lời giải:
Do vòng quay Mặt Trời quay mỗi vòng khoảng 15 phút và chuyển động theo chiều kim đồng hồ nên sau 15 phút, bán kính của vòng quay quét một góc lượng giác có số đo bằng – 2π (rad).
Do đó, sau 10 phút, bán kính của vòng quay quét một góc lượng giác có số đo bằng (rad).
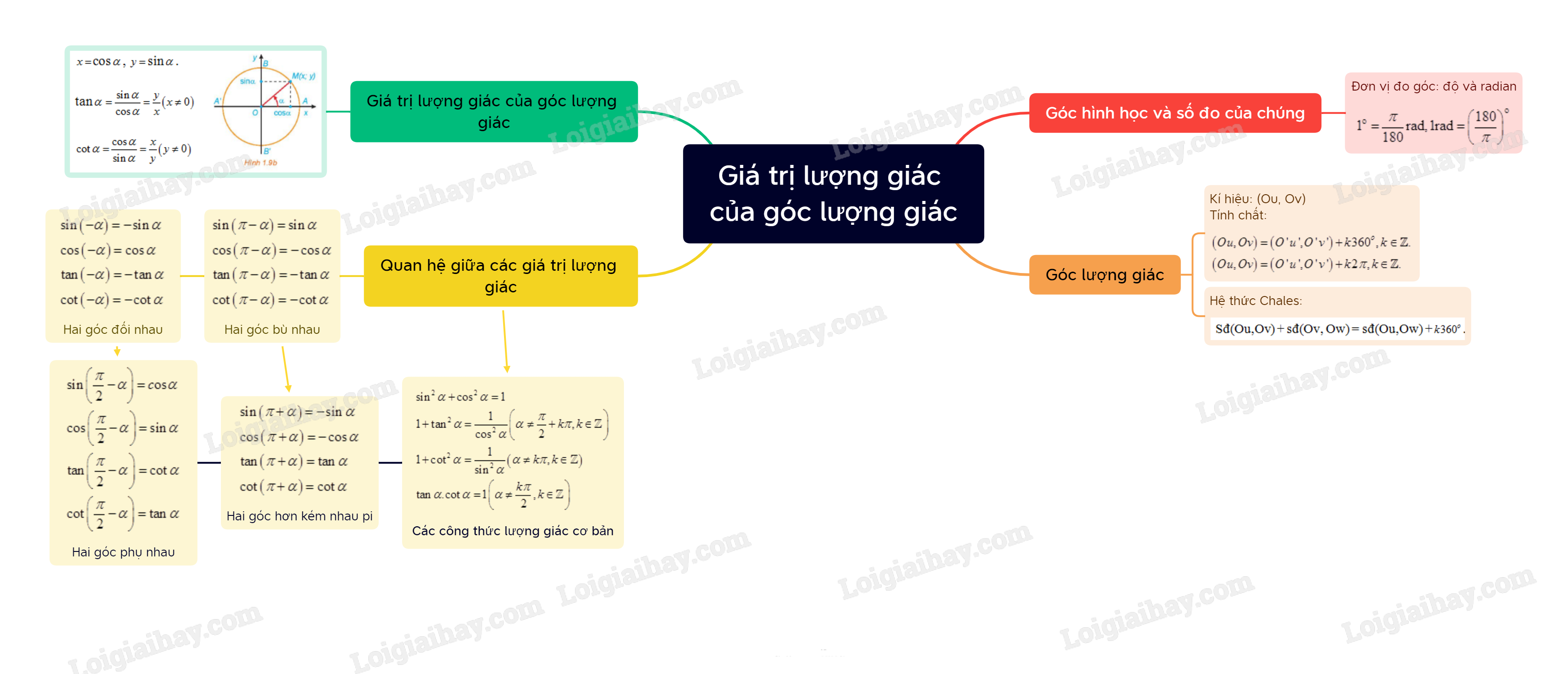
Lý thuyết Góc lượng giác. Giá trị lượng giác của góc lượng giác
I. Góc lượng giác
1. Góc hình học và số đo của chúng
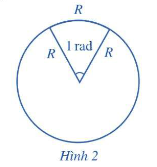
*Nhận xét:
- Đơn vị đo góc: độ hoặc radian (rad).
- Ta có: rad, do đó 1 rad , rad.
- Người ta thường không viết chữ radian hay rad sau số đo góc.
VD: rad cũng được viết là .
2. Góc lượng giác và số đo của chúng
a, Khái niệm
- Cho 2 tia Ou, Ov. Nếu tia Om quay chỉ theo chiều dương (hay chỉ theo chiều âm) xuất phát từ Ou đến trùng với tia Ov thì ta nói: Tia Om quét một góc lượng giác với tia đầu Ou và tia cuối Ov.
Kí hiệu: (Ou, Ov).
- Mỗi góc lượng giác được xác định bởi tia đầu Ou, tia cuối Ov và số đo của góc đó.
b, Tính chất
- Cho hai góc lượng giác = và (O’u’,O’v’) có tia đầu trùng nhau , tia cuối trùng nhau .
Khi đó, nếu sử dụng đợn vị đo là độ thì ta có:
Nếu sử dụng đơn vị đo là radian thì:
* Hệ thức Chasles
Với 3 tia Ou, Ov, Ow bất kì ta có:
(Ou,Ov) + (Ov, Ow) = (Ou,Ow)
II. Giá trị lượng giác của góc lượng giác
1. Đường tròn lượng giác
Trong mặt phẳng toa độ đã được định hướng Oxy, lấy điểm A(1;0). Đường tròn tâm O, bán kính OA = 1 được gọi là đường tròn lượng giác (hay đường tròn đơn vị) gốc A.
2. Giá trị lượng giác của góc lượng giác
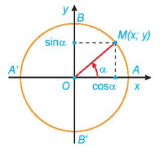
- Trục tung là trục sin, trục hoành là trục côsin.
- Điểm M(x;y) nằm trên đường tròn như hình vẽ. Khi đó:
cos, sin.
tan
* Dấu của các giá trị lượng giác của góc
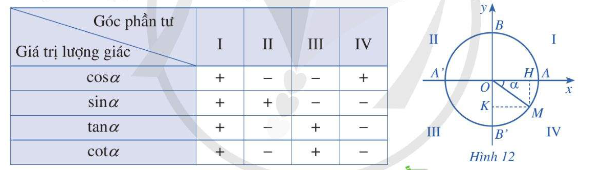
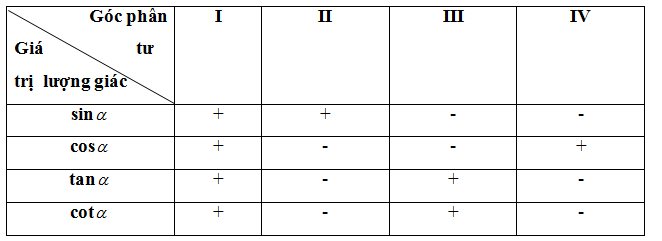
* Các công thức lượng giác cơ bản
3. Giá trị lượng giác của các góc có liên quan đặc biệt
- Hai góc đối nhau và
- Hai góc bù nhau ( và -)
- Hai góc phụ nhau ( và -)
- Hai góc hơn kém ( và + )
4. Sử dụng máy tính cầm tay để tính giá trị của một góc lượng giác
Đơn vị độ:

Đơn vị radian:

Xem thêm Lời giải bài tập SBT Toán 11 sách Cánh diều hay, chi tiết khác:
Bài 2: Các phép biến đổi lượng giác
Bài 3: Hàm số lượng giác và đồ thị
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Cánh diều (hay nhất)
- Văn mẫu lớp 11 - Cánh diều
- Tóm tắt tác phẩm Ngữ văn 11 – Cánh diều
- Tác giả tác phẩm Ngữ văn 11 - Cánh diều
- Giải SBT Ngữ văn 11 – Cánh diều
- Bố cục tác phẩm Ngữ văn 11 – Cánh diều
- Giải Chuyên đề học tập Ngữ văn 11 – Cánh diều
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Cánh diều
- Soạn văn 11 Cánh diều (ngắn nhất)
- Giải sgk Tiếng Anh 11 – ilearn Smart World
- Giải sbt Tiếng Anh 11 - ilearn Smart World
- Trọn bộ Từ vựng Tiếng Anh 11 ilearn Smart World đầy đủ nhất
- Giải sgk Vật lí 11 – Cánh diều
- Lý thuyết Vật lí 11 – Cánh diều
- Giải sbt Vật lí 11 – Cánh diều
- Giải Chuyên đề học tập Vật lí 11 – Cánh diều
- Giải sgk Hóa học 11 – Cánh diều
- Giải Chuyên đề học tập Hóa học 11 – Cánh diều
- Lý thuyết Hóa 11 - Cánh diều
- Giải sbt Hóa học 11 – Cánh diều
- Giải sgk Sinh học 11 – Cánh diều
- Lý thuyết Sinh học 11 – Cánh diều
- Giải Chuyên đề học tập Sinh học 11 – Cánh diều
- Giải sbt Sinh học 11 – Cánh diều
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Cánh diều
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Cánh diều
- Lý thuyết Kinh tế pháp luật 11 – Cánh diều
- Giải sbt Kinh tế pháp luật 11 – Cánh diều
- Giải sgk Lịch sử 11 – Cánh diều
- Giải Chuyên đề học tập Lịch sử 11 – Cánh diều
- Lý thuyết Lịch sử 11 - Cánh diều
- Giải sbt Lịch sử 11 – Cánh diều
- Giải sgk Địa lí 11 – Cánh diều
- Giải Chuyên đề học tập Địa lí 11 – Cánh diều
- Lý thuyết Địa lí 11 - Cánh diều
- Giải sbt Địa lí 11 – Cánh diều
- Giải sgk Công nghệ 11 – Cánh diều
- Lý thuyết Công nghệ 11 - Cánh diều
- Giải sbt Công nghệ 11 – Cánh diều
- Giải sgk Tin học 11 – Cánh diều
- Giải Chuyên đề học tập Tin học 11 – Cánh diều
- Lý thuyết Tin học 11 - Cánh diều
- Giải sbt Tin học 11 – Cánh diều
- Giải sgk Giáo dục quốc phòng an ninh 11 – Cánh diều
- Lý thuyết Giáo dục quốc phòng 11 – Cánh diều
- Giải sbt Giáo dục quốc phòng 11 – Cánh diều
- Giải sgk Hoạt động trải nghiệm 11 – Cánh diều