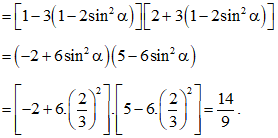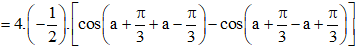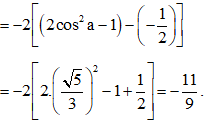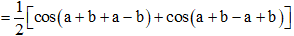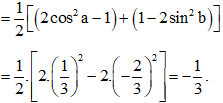Sách bài tập Toán 11 Bài 2 (Cánh diều): Các phép biến đổi lượng giác
Với giải sách bài tập Toán 11 Bài 2: Các phép biến đổi lượng giác sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 11 Bài 2.
Giải SBT Toán 11 Bài 2: Các phép biến đổi lượng giác
Lời giải:
Đáp án đúng là: A
Ta có tan(a+b)=tana+tanb1−tana.tanb=17+341−17.34=25282528=1 .
Bài 16 trang 14 SBT Toán 11 Tập 1: Nếu sinα=1√3 với 0<α<π2 thì giá trị của cos(α+π3) bằng:
Lời giải:
Đáp án đúng là: A
Vì 0<α<π2 nên cos α > 0, do đó từ sin2 α + cos2 α = 1, suy ra
cosα=√1−sin2α=√1−(1√3)2=√63.
Ta có cos(α+π3)=cosαcosπ3−sinα sinπ3=√63.12−1√3.√32=√66−12 .
Lời giải:
Đáp án đúng là: D
Ta có P=(1−3cos2α)(2+3cos2α)
Bài 18 trang 15 SBT Toán 11 Tập 1: Chọn đẳng thức đúng trong các đẳng thức sau:
Lời giải:
Đáp án đúng là: B
Ta có sin4 x + cos4 x = 1 – 2sin2 x cos2 x (theo Bài 9a)
= 1 – 2 (sin x cos x)2 = 1−2(sin2x2)2=1−2.sin22x4=1−2(1−cos22x)4
=1−2−2cos22x4=4−2+2cos22x4=3+(2cos22x−1)4=3+cos4x4.
Vậy sin4x+cos4x=3+cos4x4 .
Lời giải:
Đáp án đúng là: A
Ta có cos(120° – x) + cos(120° + x) – cos x
= cos 120° cos x + sin 120° sin x + cos 120° cos x – sin 120° sin x – cos x
= 2 cos 120° cos x – cos x
= 2 . (−12) . cos x – cos x
= – cos x – cos x
= – 2 cos x.
Bài 20 trang 15 SBT Toán 11 Tập 1: Nếu cosa=34 thì giá trị của cosa2cosa2 bằng:
Lời giải:
Đáp án đúng là: B
Ta có cosa2cosa2=cos2a2=1+cos2.a22=1+cosa2=1+342=78 .
Lời giải:
Đáp án đúng là: A
Ta có A=4sin(a+π3)sin(a−π3)
=−2(cos2a−cos2π3)
Bài 22 trang 15 SBT Toán 11 Tập 1: Nếu cosa=13, sinb=−23 thì giá trị cos(a + b) cos(a − b) bằng:
Lời giải:
Đáp án đúng là: D
Ta có cos(a + b) cos(a − b)
=12(cos2a+cos2b)
Bài 23 trang 15 SBT Toán 11 Tập 1: Giá trị của biểu thức P=sinπ9+sin5π9cosπ9+cos5π9 bằng:
Lời giải:
Đáp án đúng là: C
Ta có P=sinπ9+sin5π9cosπ9+cos5π9=2sinπ9+5π92cosπ9−5π922cosπ9+5π92cosπ9−5π92
=sinπ3cos(−2π9)cosπ3cos(−2π9)=sinπ3cosπ3=√3212=√3.
Lời giải:
Đáp án đúng là: C
Ta có A=sinx+sin2x+sin3xcosx+cos2x+cos3x =(sinx+sin3x)+sin2x(cosx+cos3x)+cos2x
=2sinx+3x2cosx−3x2+sin2x2cosx+3x2cosx−3x2+cos2x =2sin2xcos(−x)+sin2x2cos2xcos(−x)+cos2x
=sin2x(2cosx+1)cos2x(2cosx+1)=sin2xcos2x=tan2x.
Bài 25 trang 15 SBT Toán 11 Tập 1: Cho sina=23 với π2<a<π . Tính:
b) sin(a+π4), cos(a−5π6), tan(a+2π3) ;
Lời giải:
a) Vì π2<a<π nên cos a < 0, do đó từ sin2 a + cos2 a = 1, suy ra
cosa=−√1−sin2a=−√1−(23)2=−√53.
Ta có tana=sinacosa=23−√53=−2√55.
b) sin(a+π4)=sinacosπ4+cosasinπ4=23.√22+(−√53).√22=2√2−√106 .
cos(a−5π6)=cosacos5π6+sinasin5π6=(−√53).(−√32)+23.12=√15+26.
tan(a+2π3)=tana+tan2π31−tanatan2π3=−2√55+(−√3)1−(−2√55).(−√3)=8√5+9√37.
c) sin2a=2sinacosa=2.23.(−√53)=−4√59 .
cos2a=2cos2a−1=2.(−√53)2−1=19.
Bài 26 trang 15 SBT Toán 11 Tập 1: Cho cos a = 0,2 với π < a < 2π. Tính sina2 , cosa2 , tana2 .
Lời giải:
Do π < a < 2π nên π2<a2<π . Suy ra sina2>0, cosa2<0 .
Ta có: sin2a2=1−cosa2=1−0,22=0,4 , suy ra sina2=√105 .
Do đó, cosa2=−√1−sin2a2=−√1−(√105)2=−√155 .
tana2=sina2cosa2=√105−√155=−√63.
Bài 27 trang 15 SBT Toán 11 Tập 1: Cho tana2=1√2 . Tính sin a, cos a, tan a.
Lời giải:
Ta có sina=2sina2cosa2=2sina2cosa2sin2a2+cos2a2 (do sin2a2+cos2a2=1 )
=2tana2tan2a2+1=2.1√2(1√2)2+1=2√23.
cosa=cos2a2−sin2a2=cos2a2−sin2a2sin2a2+cos2a2=1−tan2a2tan2a2+1=1−(1√2)2(1√2)2+1=13.
tana=sinacosa=2√2313=2√2.
Lời giải:
Ta có cos(a + 2b) = 2cos a
⇔ cos[(a + b) + b] = 2cos[(a + b) – b]
⇔ cos(a + b) . cos b – sin(a + b) . sin b = 2[cos(a + b) . cos b + sin(a + b) . sin b]
⇔ cos(a + b) . cos b – 2 cos(a + b) . cos b = 2 sin(a + b) . sin b + sin(a + b) . sin b
⇔ – cos(a + b) . cos b = 3 sin(a + b) . sin b
⇔ sin(a + b) . sin b = −13 cos(a + b) . cos b
⇔sin(a+b)sinbcos(a+b)cosb=−13
⇔ tan(a + b) tan b = −13 .
Bài 29 trang 16 SBT Toán 11 Tập 1: Cho tam giác ABC, chứng minh rằng:
a) tan A + tan B + tan C = tan A . tan B . tan C (với điều kiện tam giác ABC không vuông);
b) tanA2.tanB2+tanB2.tanC2+tanC2.tanA2=1 .
Lời giải:
a) Vì tam giác ABC không vuông nên A, B, C khác π2 , do đó tan A, tan B, tan C xác định.
Do A + B + C = π nên A + B = π – C, do đó tan(A + B) = tan(π – C) = tan(– C) = – tanC.
Mà tan(A+B)=tanA+tanB1−tanAtanB .
Khi đó tanA+tanB1−tanA tanB=−tanC
⇔ tan A + tan B = – tan C . (1 – tan A . tan B)
⇔ tan A + tan B = – tan C + tan A . tan B . tan C
⇔ tan A + tan B + tan C = tan A . tan B . tan C.
b) Ta có A+B+C2=π2 , suy ra A2+B2=π2−C2 nên tan(A2+B2)=cotC2
⇔tanA2+tanB21−tanA2.tanB2=1tanC2
⇔(tanA2+tanB2)tanC2=1−tanA2.tanB2
⇔tanA2.tanC2+tanB2.tanC2+tanA2.tanB2=1
⇔tanA2.tanB2+tanB2.tanC2+tanC2.tanA2=1.
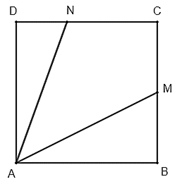
b) Góc chiếu sáng của đèn pin bằng bao nhiêu độ?
Lời giải:
a) Trong tam giác vuông ABM, có tan^BAM=BMBA=12 .
Trong tam giác vuông ADN, có tan^DAN=DNAD=DNDC=13 .
Do đó, tan(^BAM+^DAN)=tan^BAM+tan^DAN1−tan^BAM.tan^DAN=12+131−12.13=1 .
b) Từ câu a) ta có tan(^BAM+^DAN) = 1 nên ^BAM+^DAN=45° .
Suy ra .
Vậy góc chiếu sáng của đèn pin bằng 45°.
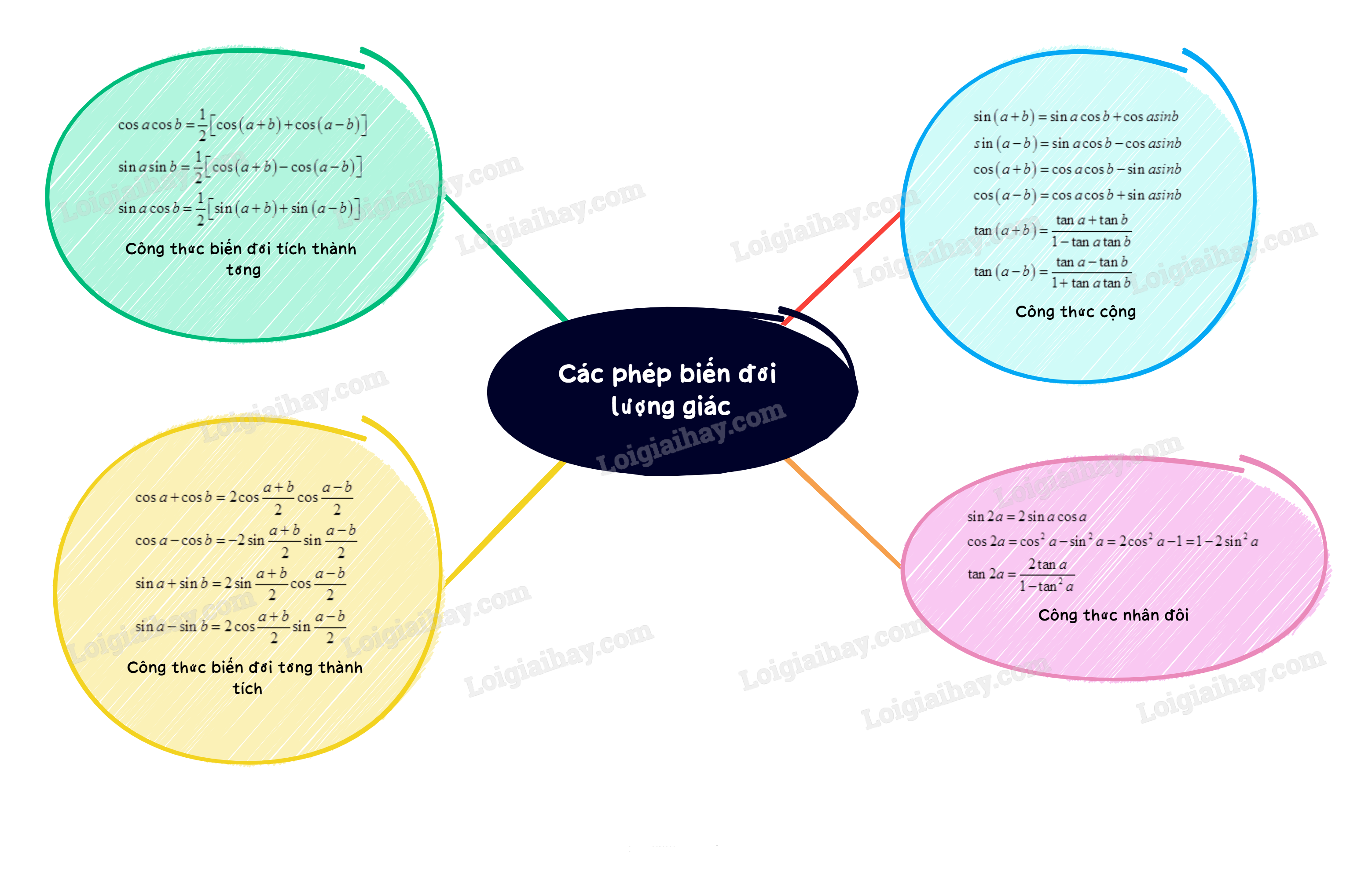
Lý thuyết Các phép biến đổi lượng giác
I. Công thức cộng
II. Công thức nhân đôi
Suy ra, công thức hạ bậc:
III. Công thức biến đổi tích thành tổng
IV. Công thức biến đổi tổng thành tích
Xem thêm Lời giải bài tập SBT Toán 11 sách Cánh diều hay, chi tiết khác:
Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác
Bài 3: Hàm số lượng giác và đồ thị
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Cánh diều (hay nhất)
- Văn mẫu lớp 11 - Cánh diều
- Tóm tắt tác phẩm Ngữ văn 11 – Cánh diều
- Tác giả tác phẩm Ngữ văn 11 - Cánh diều
- Giải SBT Ngữ văn 11 – Cánh diều
- Bố cục tác phẩm Ngữ văn 11 – Cánh diều
- Giải Chuyên đề học tập Ngữ văn 11 – Cánh diều
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Cánh diều
- Soạn văn 11 Cánh diều (ngắn nhất)
- Giải sgk Tiếng Anh 11 – ilearn Smart World
- Giải sbt Tiếng Anh 11 - ilearn Smart World
- Trọn bộ Từ vựng Tiếng Anh 11 ilearn Smart World đầy đủ nhất
- Giải sgk Vật lí 11 – Cánh diều
- Lý thuyết Vật lí 11 – Cánh diều
- Giải sbt Vật lí 11 – Cánh diều
- Giải Chuyên đề học tập Vật lí 11 – Cánh diều
- Giải sgk Hóa học 11 – Cánh diều
- Giải Chuyên đề học tập Hóa học 11 – Cánh diều
- Lý thuyết Hóa 11 - Cánh diều
- Giải sbt Hóa học 11 – Cánh diều
- Giải sgk Sinh học 11 – Cánh diều
- Lý thuyết Sinh học 11 – Cánh diều
- Giải Chuyên đề học tập Sinh học 11 – Cánh diều
- Giải sbt Sinh học 11 – Cánh diều
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Cánh diều
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Cánh diều
- Lý thuyết Kinh tế pháp luật 11 – Cánh diều
- Giải sbt Kinh tế pháp luật 11 – Cánh diều
- Giải sgk Lịch sử 11 – Cánh diều
- Giải Chuyên đề học tập Lịch sử 11 – Cánh diều
- Lý thuyết Lịch sử 11 - Cánh diều
- Giải sbt Lịch sử 11 – Cánh diều
- Giải sgk Địa lí 11 – Cánh diều
- Giải Chuyên đề học tập Địa lí 11 – Cánh diều
- Lý thuyết Địa lí 11 - Cánh diều
- Giải sbt Địa lí 11 – Cánh diều
- Giải sgk Công nghệ 11 – Cánh diều
- Lý thuyết Công nghệ 11 - Cánh diều
- Giải sbt Công nghệ 11 – Cánh diều
- Giải sgk Tin học 11 – Cánh diều
- Giải Chuyên đề học tập Tin học 11 – Cánh diều
- Lý thuyết Tin học 11 - Cánh diều
- Giải sbt Tin học 11 – Cánh diều
- Giải sgk Giáo dục quốc phòng an ninh 11 – Cánh diều
- Lý thuyết Giáo dục quốc phòng 11 – Cánh diều
- Giải sbt Giáo dục quốc phòng 11 – Cánh diều
- Giải sgk Hoạt động trải nghiệm 11 – Cánh diều