Nội dung bài viết

    Xem thêm

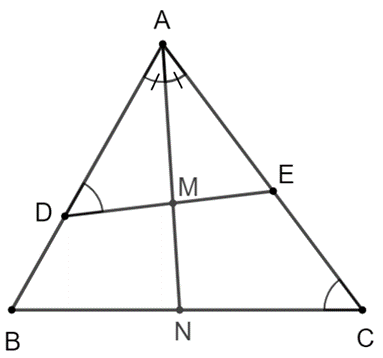
    Cho tam giác ABC có ba góc nhọn. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho

    Lời giải Bài 13 trang 65 SBT Toán 8 Tập 2 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8.

    1 282 16/11/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 8 Bài 2: Các trường hợp đồng dạng của hai tam giác

    Bài 13 trang 65 SBT Toán 8 Tập 2: Cho tam giác ABC có ba góc nhọn. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho ADE^=ACB^.

    a) Chứng minh rằng ∆AED ᔕ ∆ABC.

    b) Tia phân giác của BAC^ cắt DE tại M và cắt BC tại N.

    Chứng minh rằng ME . NC = MD . NB.

    Lời giải:

    Cho tam giác ABC có ba góc nhọn. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E

    a) Xét ∆AED và ∆ABC có

    A^ chung; ADE^=ACB^.

    Do đó ∆AED ᔕ ∆ABC (g.g)

    b) Ta có ∆AED ᔕ ∆ABC suy ra AEAB=ADAC hay AEAD=ABAC (1)

    • Vì AM là tia phân giác của DAE^ nên MEMD=AEAD (2)

    • Vì AN là tia phân giác của BAC^ nên NBNC=ABAC (3)

    Từ (1); (2) và (3) suy ra MEMD=NBNC hay ME . NC = MD . NB (đpcm).

    Xem thêm lời giải Sách bài tập Toán 8 bộ sách Chân trời sáng tạo hay, chi tiết khác:

    Bài 1 trang 62 SBT Toán 8 Tập 2: Tam giác ABC có độ dài AB = 9 cm, AC = 12 cm, BC = 14 cm...

    Bài 2 trang 62 SBT Toán 8 Tập 2: a) Tam giác ABC và MBN (Hình 4) có đồng dạng với nhau không? Vì sao?....

    Bài 3 trang 63 SBT Toán 8 Tập 2: Cho tam giác MAB và ABN như Hình 5. Biết MA = 10 cm, MB = 15 cm...

    Bài 4 trang 63 SBT Toán 8 Tập 2: Anh Minh dự định thiết kế sân vườn nhà mình có hai bồn hoa hình tam giác đồng dạng...

    Bài 5 trang 63 SBT Toán 8 Tập 2: Quan sát Hình 7. Chứng minh rằng...

    Bài 6 trang 63 SBT Toán 8 Tập 2: Quan sát Hình 8. a) Chứng minh rằng ∆ABC ᔕ ∆DEF....

    Bài 7 trang 63 SBT Toán 8 Tập 2: Cho tam giác ABC có AB = 12, AC = 15. Lấy điểm M thuộc cạnh AB và điểm NN..

    Bài 8 trang 64 SBT Toán 8 Tập 2: Cho tam giác đều ABC, từ B và C kẻ các đường thẳng song song với AC và AB,...

    Bài 9 trang 64 SBT Toán 8 Tập 2: Quan sát Hình 9. a) Chứng minh rằng ∆ABC ᔕ ∆MNQ....

    Bài 10 trang 64 SBT Toán 8 Tập 2: Trong Hình 10, cho biết AB = 4,2;...

    Bài 11 trang 64 SBT Toán 8 Tập 2: Quan sát Hình 11. Vẽ vào tờ giấy tam giác MNP với NP = 6 cm...

    Bài 12 trang 64 SBT Toán 8 Tập 2: Trong Hình 12, cho tứ giác ABCD là hình thang....

    Bài 13 trang 65 SBT Toán 8 Tập 2: Cho tam giác ABC có ba góc nhọn. Trên cạnh AB lấy điểm D,...

    Xem thêm lời giải Sách bài tập Toán 8 bộ sách Chân trời sáng tạo hay, chi tiết khác:

    Bài 3: Các trường hợp đồng dạng của hai tam giác vuông

    Bài 4: Hai hình đồng dạng

    Bài tập cuối chương 8 trang 73

    Bài 1: Mô tả xác suất bằng tỉ số

    Bài 2: Xác suất lí thuyết và xác suất thực nghiệm

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 282 16/11/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: