Bài 10 trang 21 Toán 11 Tập 1 | Cánh diều Giải Toán 11

Lời giải Bài 10 trang 21 Toán 11 Tập 1 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 Tập 1.

1 665 02/11/2023

Trang trước

Trang sau

Giải Toán 11 Bài 2: Các phép biến đổi lượng giác

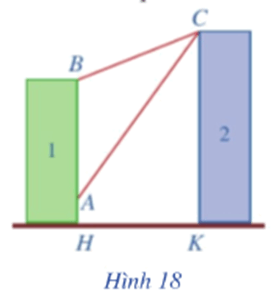
Bài 10 trang 21 Toán 11 Tập 1: Có hai chung cư cao tầng xây cạnh nhau với khoảng cách giữa chúng là HK = 20 m. Để đảm bảo an ninh, trên nóc chung cư thứ hai người ta lắp camera ở vị trí C. Gọi A, B lần lượt là vị trí thấp nhất, cao nhất trên chung cư thứ nhất mà camera có thể quan sát được (Hình 18). Hãy tính số đo góc ACB (phạm vi camera có thể quan sát được ở chung cư thứ nhất). Biết rằng chiều cao của chung cư thứ hai là CK = 32 m, AH = 6 m, BH = 24 m (làm tròn kết quả đến hàng phần mười theo đơn vị độ).

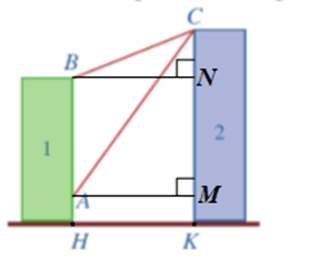
Bài 10 trang 21 Toán 11 Tập 1 | Cánh diều Giải Toán 11

Lời giải:

Bài 10 trang 21 Toán 11 Tập 1 | Cánh diều Giải Toán 11

Kẻ AM ⊥ CK, BN ⊥CK (hình vẽ) ta có:

BN = AM = HK = 20 (m);

CN = CK – NK = CK – BH = 32 – 24 = 8 (m);

MN = AB = BH – AH = 24 – 6 = 18 (m);

CM = CN + MN = 8 + 18 = 26 (m).

Đặt $\hat{B C N} = α, \hat{A C M} = β$ .

Xét $∆$ BCN vuông tại N có: tan $α = \frac{B N}{C N} = \frac{20}{8} = \frac{5}{2}$ ;

Xét $∆$ ACM vuông tại M có: tan $β = \frac{A M}{C M} = \frac{20}{26} = \frac{10}{13}$ ;

Ta có: tan $\hat{A C B} = \tan (\hat{B C N} - \hat{A C M}) = \tan (α - β)$

$\Rightarrow \tan \hat{A C B} = \frac{\tan α - \tan β}{1 + \tan α \tan β} = \frac{\frac{5}{2} - \frac{10}{13}}{1 + \frac{5}{2} . \frac{10}{13}} = \frac{45}{76}$ .

$\Rightarrow \hat{A C B} \approx 0, 01 °$ .

Vậy góc ACB (phạm vi camera có thể quan sát được ở chung cư thứ nhất) có số đo xấp xỉ 0,01°.

Xem thêm lời giải bài tập Toán 11 Cánh diều hay, chi tiết khác:

Câu hỏi khởi động trang 16 Toán 11 Tập 1: Ở lớp dưới, ta đã làm quen với một số phép tính trong tập hợp các số thực, chẳng hạn...

Hoạt động 1 trang 16 Toán 11 Tập 1: a) Cho $a = \frac{π}{6}, b = \frac{π}{3}$ . Hãy tính sina, cosa, sinb, cosb và sin(a + b). Từ đó rút ra đẳng thức sin(a + b) = sina cosb + cosa sinb (*)...

Luyện tập 1 trang 16 Toán 11 Tập 1: Tính sin $\frac{π}{12}$ ...

Hoạt động 2 trang 17 Toán 11 Tập 1: a) Tính cos(a + b) bằng cách biến đổi cos(a + b) = sin $(\frac{π}{2} - (a + b)) = \sin ((\frac{π}{2} - a) - b)$ và sử dụng công thức cộng đối với sin...

Luyện tập 2 trang 17 Toán 11 Tập 1: Tính cos15°...

Hoạt động 3 trang 17 Toán 11 Tập 1: a) Sử dụng công thức cộng đối với sin và côsin, hãy tính tan(a + b) theo tana và tanb khi các biểu thức đều có nghĩa...

Luyện tập 3 trang 17 Toán 11 Tập 1: Tính tan165°...

Hoạt động 4 trang 18 Toán 11 Tập 1: Tính sin2a, cos2a, tan2a bằng cách thay b = a trong công thức cộng...

Luyện tập 4 trang 18 Toán 11 Tập 1: Cho tan $\frac{a}{2}$ = -2. Tính tana...

Luyện tập 5 trang 18 Toán 11 Tập 1: Tính: sin $\frac{π}{8}$ , cos $\frac{π}{8}$ ...

Hoạt động 5 trang 18 Toán 11 Tập 1: Sử dụng công thức cộng, rút gọn mỗi biểu thức sau:

cos(a + b) + cos(a – b); cos(a + b) – cos(a – b); sin(a + b) + sin(a – b)...

Luyện tập 6 trang 19 Toán 11 Tập 1: Cho cosa = $\frac{2}{3}$ . Tính B = cos $\frac{3 a}{2}$ cos $\frac{a}{2}$ ...

Hoạt động 6 trang 19 Toán 11 Tập 1: Sử dụng công thức biến đổi tích thành tổng và đặt a + b = u; a − b = v rồi biến đổi các biểu thức sau thành tích...

Luyện tập 7 trang 19 Toán 11 Tập 1: Tính: D = $\frac{\sin \frac{7 π}{9} + \sin \frac{π}{9}}{cos \frac{7 π}{9} - \cos \frac{π}{9}}$ ...

Bài 1 trang 20 Toán 11 Tập 1: Cho cosa = $\frac{3}{5}$ với 0<a< $\frac{π}{2}$ . Tính sin $(a + \frac{π}{6})$ , cos $(a - \frac{π}{3})$ , tan $(a + \frac{π}{4})$ ...

Bài 2 trang 20 Toán 11 Tập 1: Tính: A = sin(a – 17°)cos(a + 13°) – sin(a + 13°)cos(a – 17°);...

Bài 3 trang 20 Toán 11 Tập 1: Cho tan(a + b) = 3, tan(a – b) = 2. Tính: tan2a, tan2b...

Bài 4 trang 20 Toán 11 Tập 1: Cho sina = $\frac{2}{\sqrt{5}}$ . Tính cos2a, cos4a...

Bài 5 trang 20 Toán 11 Tập 1: Cho sina + cosa = 1. Tính: sin2a...

Bài 6 trang 21 Toán 11 Tập 1: Cho cos2a = $\frac{1}{3}$ với $\frac{π}{2}$ <a< $π$ . Tính: sina, cosa, tana...

Bài 7 trang 21 Toán 11 Tập 1: Cho cos2x = $\frac{1}{4}$ . Tính: A = cos $(x + \frac{π}{6})$ cos $(x - \frac{π}{6})$ ; B = sin $(x + \frac{π}{3})$ sin $(x - \frac{π}{3})$ ...

Bài 8 trang 21 Toán 11 Tập 1: Rút gọn biểu thức: A = $\frac{\sin x + \sin 2 x + \sin 3 x}{\cos x + \cos 2 x + \cos 3 x}$ ...

Bài 9 trang 21 Toán 11 Tập 1: Một sợi cáp R được gắn vào một cột thẳng đứng ở vị trí cách mặt đất 14 m. Một sợi cáp S khác cũng được gắn vào cột đó ở vị trí cách mặt đất 12 m...

Bài 10 trang 21 Toán 11 Tập 1: Có hai chung cư cao tầng xây cạnh nhau với khoảng cách giữa chúng là HK = 20 m...

Xem thêm lời giải bài tập Toán 11 Cánh diều hay, chi tiết khác:

Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác

Bài 2: Các phép biến đổi lượng giác

Bài 3: Hàm số lượng giác và đồ thị

Bài 4: Phương trình lượng giác cơ bản

Bài tập cuối chương 1

1 665 02/11/2023

Trang trước

Trang sau

Xem thêm các chương trình khác: