Nội dung bài viết

    Xem thêm

    Tính diện tích S của hình thang ABCD theo x bằng hai cách

    Với giải Bài 6 trang 9 SGK Toán lớp 8 tập 2 được biên soạn lời giải chi tiết sẽ giúp học sinh biết cách làm bài tập môn Toán 8. Mời các bạn đón xem:

    1 788 26/04/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 8 Bài 2: Phương trình bậc nhất một ẩn và cách giải

    Video Giải Bài 6 trang 9 Toán 8 Tập 2

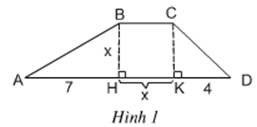
    Bài 6 trang 9 Toán 8 Tập 2: Tính diện tích S của hình thang ABCD theo x bằng hai cách:

    1) Tính theo công thức: S = BH x (BC + DA) : 2

    2) S = SABH + SBCKH + SCKD

    Sau đó, sử dụng giả thiết S = 20 để thu được hai phương trình tương đương với nhau. Trong hai phương trình ấy, có phương trình nào là phương trình bậc nhất không?

    Tính diện tích S của hình thang ABCD theo x bằng hai cách (ảnh 1)

    Lời giải:

    1) Công thức: S = BH x (BC + DA) : 2

    + Có BH ⊥ HK, CK ⊥ HK (giả thiết)

    Mà BC // HK (vì ABCD là hình thang)

    Do đó: BH ⊥ BC, CK ⊥ BC

    Tứ giác BCKH có bốn góc vuông nên BCKH là hình chữ nhật.

    Mặt khác: BH = HK = x (giả thiết) nên BCKH là hình vuông.

    ⇒ BH = BC = CK = KH = x

    + AD = AH + HK + KD = 7 + x + 4 = 11 + x.

    Vậy S = BH x (BC + DA) : 2 = x.(x + 11 + x) : 2

    = x.(2x + 11) : 2 = 2x2+11x2.

    2) S = SABH + SBCKH + SCKD

    + ABH là tam giác vuông tại H

    ⇒ SBAH = 12 .BH.AH = 12.7.x = 7x2.

    + BCKH là hình chữ nhật

    ⇒ SBCKH = x.x = x2.

    + CKD là tam giác vuông tại K

    ⇒ SCKD = 12.CK.KD = 12.4.x = 2x.

    Do đó: S = SABH + SBCKH + SCKD 

    = 7x2 + x2 + 2x = x2 + 11x2.

    - Với S = 20 ta có phương trình:

    Theo cách tính 1 ta có:   2x2+11x2 = 20.

    Theo cách tín 2 ta có: x2 + 11x2  = 20

    Hai phương trình trên tương đương với nhau. Và cả hai phương trình trên đều không phải là phương trình bậc nhất.

    Xem thêm lời giải bài tập Toán lớp 8 hay, chi tiết khác:

    Câu hỏi 1 trang 8 Toán 8 Tập 2: Giải các phương trình x – 4 = 0...

    Câu hỏi 2 trang 8 Toán 8 Tập 2: Giải các phương trình 0,1x = 1,5...

    Câu hỏi 3 trang 9 Toán 8 Tập 2: Giải phương trình: -0,5x + 2,4 = 0...

    Bài 7 trang 10 Toán 8 Tập 2: Hãy chỉ ra các phương trình bậc nhất trong các phương trình sau...

    Bài 8 trang 10 Toán 8 Tập 2: Giải các phương trình 4x – 20 = 0...

    Bài 9 trang 10 Toán 8 Tập 2: Giải các phương trình sau, viết số gần đúng của mỗi nghiệm ở dạng số thập phân...

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 788 26/04/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: