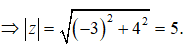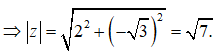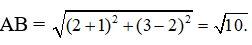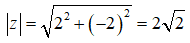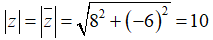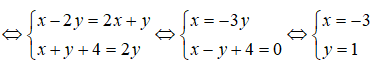Số phức là gì? Lý thuyết, tính chất và cách giải các dạng bài tập (2024) chi tiết nhất

SỐ PHỨC

I. Lý thuyết số phức

1. Số phức là gì?

Số phức là số được viết dưới dạng a + bi trong đó a, b là số thực và i² = -1 hay i = $\sqrt{-1}$. Trong đó a, b là các số thực, i là đơn vị ảo, a là phần thực và b gọi là phần ảo.

2. Các loại số phức

a) Số phức liên hợp

Định nghĩa: Số phức liên hợp có dạng: Z = a + bi trong đó số phức $\overline{z}=a + bi$được gọi là số phức liên hợp của Z

Số phức liên hợp có 1 số tính chất như sau:

Zx$\overline{z}$ = a² + b² là một số thực

Z + $\overline{z}$ = 2a là một số thực

$\overline{z}$ + $\overline{z\text{'}}$ = $\overline{z + Z\text{'}}$

b) Số phức nghịch đảo

Có thể nói, số phức nghịch đảo hay nghịch đảo của số phức Z kí hiệu là Z ^-1 là số phức có dạng sao cho tích của số phức nghịch đảo với số phức Z bằng 1

- Số phức dạng nghịch đảo của Z = a +bi là số phức Z ^-1 = $\frac{1}{Z}$ = $\frac{1}{a + bi}$

Số nghịch đảo của Z = a +bi khác 0 là số Z ^-1 = $\frac{1}{Z}$ = $\frac{\overline{z}}{\left|Z^2\right|}$

c) Số phức thuần ảo

Số phức thuần ảo là khi có phần thực a = 0 thì Z = bi thuộc R. Khi đó thì Z được gọi là số thuần ảo

d) Modun số phức

Modun của số phức Z = a +bi là độ dài của vecto u (a, b) biểu diễn số phức đó.

Theo định nghĩa khác thì số phức của modun Z = a +bi trong đó a,b thuộc R là căn bậc hai của số học của a² + b²

Ví dụ: 3 +4i = 25

=> |z| = 3 +4i = 5

Ta dễ dàng thấy trị tuyệt đối của số thực cũng chính là modun của số thực đó. Do đó thì đôi khi ta cũng có thể gọi là modun của số phức là trị tuyệt đối của số phức.

Về mặt hình học thì mỗi số phức Z = a +bi với a,b thuộc R được biểu diễn bởi một điểm M (z) = (a, b) trên mặt phẳng O (xy) và ngược lại. Khi đó thì modun của Z được biểu diễn bởi độ dài đoạn thẳng OM (z). Modun của z là một số thực không âm và nó chỉ bằng 0 khi z = 0

e) Argument của số phức

Giả sử M (z) là điểm biểu diễn số phức z. Arg (z) là góc định hướng giữa chiều dương của trục thực và tia OM(z) thỏa mãn - n < Arg (z)$\le$ n.

Vậy nên nếu z = a + bi (a, b thuộc R) thì Arg(z) = Arg tan($\frac{b}{a}$)

II. Biểu diễn hình học của số phức

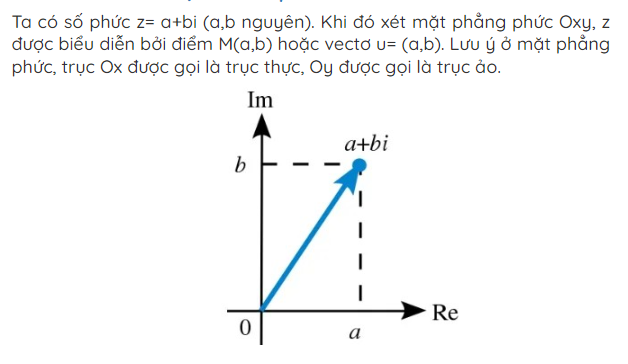
III. Các dạng bài tập số phức và cách giải

Dạng 1: Các dạng quỹ tích đơn giản căn bản

Đường thẳng: Quỹ tích các điểm M biểu diễn số phức z = x +yi là đường thẳng nếu như M (x;y) có tọa độ thỏa mãn phương trình đường thẳng: Ãx +By + C = 0

Đường tròn: QUỹ tích các điểm M biểu diễn số phức z = x + yi là đường tròn nếu như M(x; y) có tọa độ thỏa mãn phương trình đường tròn (C) : (x - a)² + (b -y)² = R². Trong đó thì I (a; b) là tâm đường trong và R là bán kính đường tròn.

Đường elip: quỹ tích các điểm M biểu diễn số phức z = x +yi là đường elip nếu như M(x; y) có tọa độ thỏa mãn phương trình đường elip (E): $\frac{x^2}{a^2}+\frac{y^2}{b^2}$ = 1 trong đó thì a,b tương ứng với các bán trục lớn và bán trục nhỏ của elip

Dạng 2: Các dạng bài tập tìm phần thực hoặc tìm phần ảo của số phức

Ta biến đổi số phưc đã cho thành z = a + bi trong đó thì a và b là các số thực. Khi đó a là phần thực của z, còn b là phần ảo của z. Chú ý các bài toán về số phwusc mà hỏi về phần ảo người ta hay có phương án nhiễu nhiều.

Dạng 3: Dạng bài tập có số phức mũ cao

Cách tính số phức mũ cao là sử dụng dạng lượng giác hoặc dạng mũ của số phức. Với dạng lượng giác của số phức ta áp dụng công thức sau:

Dạng 4: Các dạng bài tập số phức liên quan đến phương trình bậc 2 với hệ số thực

Với phương trình bậc 2 hệ số thực trên tập số phức ta chia làm 2 nhóm: Nhóm bài tập liên quan đến việc tìm nghiệm và nhóm các bài tập liên quan đến định lý vi-et. Thông thường với phương trình không có tham số ta sử dụng máy tính bỏ túi để tính ra kết quả, còn nếu có tham số thì ta tính delta và thay vào công thức nghiệm hoặc sử dụng định lý vi-et

IV. Bài tập vận dụng

1. Bài tập trắc nghiệm

Bài 1: Môđun của số phức z = -3 + 4i là

A. 5

B. -3

C. 4

D. 7

Lời giải:

Ta có: z = -3 + 4i

Bài 2: Môđun của số phức z = 2 - $\sqrt{3}$i là

A. $\sqrt{7}$

B. 2 + $\sqrt{3}$

C. 2 - $\sqrt{3}$

D. 7

Lời giải:

Ta có: z = 2 - $\sqrt{3}$i

Bài 3: Số phức z = 1 - 2i có điểm biểu diễn là

A. M (1; 2)

B. M (1; -2)

C. M (-1; 2)

D. M (-1; -2)

Lời giải:

Số phức z = 1 - 2i có điểm biểu diễn là M(1; -2).

Bài 4: Hai điểm biểu diễn hai số phức liên hợp z = 1 + i và z− = 1 - i đối xứng nhau qua

A. Trục tung

B. Trục hoành

C. Gốc tọa độ

D. Điểm I (1; -1)

Lời giải:

Bài 5: Tập hợp các điểm biểu diễn số phức z thỏa mãn |z| = 2 là

A. Hai đường thẳng

B. Đường tròn bán kính bằng 2

C. Đường tròn bán kính bằng 4

D. Hình tròn bán kính bằng 2.

Lời giải:

Bài 6: Gọi A, B là các điểm biểu diễn của các số phức z₁ = -1 + 2i, z₂ = 2 + 3i . Khi đó, độ dài đoạn thẳng AB là

A. $\sqrt{26}$

B. $\sqrt{5}+\sqrt{13}$

C. $\sqrt{10}$

D. 10

Lời giải:

Ta có: A(-1;2), B(2,3). Do đó:

Bài 7: Cho số phức z = 2 – 2i. Tìm khẳng định sai.

A. Phần thực của z là: 2.

B. Phần ảo của z là: -2.

C. Số phức liên hợp của z là z− = -2 + 2i.

D. Môđun của z là

Lời giải:

Bài 8: Cho số phức z = -1 + 3i. Phần thực, phần ảo của z− là

A. -1 và 3

B. -1 và -3

C. 1 và -3

D. -1 và -3i.

Lời giải:

Bài 9: Môđun của số phức z thỏa mãn z− = 8 - 6i là

A. 2

B. 10

C. 14

D. 2$\sqrt{7}$

Lời giải:

Ta có

Chọn đáp án B.

Bài 10: Tìm các số thực x, y sao cho (x – 2y) + (x + y + 4).i = (2x + y) + 2yi.

A. x = 3, y = 1

B. x = 3, y = -1

C. x = -3, y = -1

D. x = -3, y = 1

Lời giải:

Ta có (x – 2y) + (x + y + 4).i = (2x + y) + 2yi.

Bài 1: Hai số phức z₁ = x - 2i, z₂2 + yi (x, y ∈ R) là liên hợp của nhau khi

Lời giải:

Ta có z₁− = x + 2i. Do đó, hai số phức đã cho gọi là liên hợp của nhau khi và chỉ khi

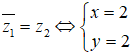
Vậy x= 2, y = 2.

Bài 2: Tập hợp các điểm biểu diễn số phức z thòa mãn |z| = |1 + i| là

Lời giải:

Ta có |1 + i| = $\sqrt{\left(1+1\right)}=\sqrt{2}$. Gọi M là điểm biểu diễn của z ta có |z| = OM.

Do đó: |z| = |1 + i| ⇔ OM = $\sqrt{2}$

Vậy tập hợp các điểm M biểu diễn số phức z là đường tròn tâm O, bán kính R= $\sqrt{2}$ .

Bài 3: Phần thực của số phức z = -i là

Lời giải:

Bài 4: Phần ảo của số phức z = -1 là

Lời giải:

Bài 5: Số phức liên hợp của số phức z = 1 + i là

Lời giải:

Bài 6: Cho z = 2i -1. Phần thực và phần ảo của z− là

Lời giải: