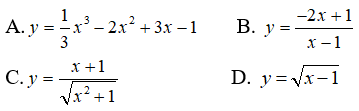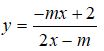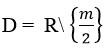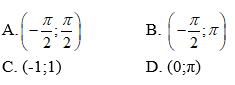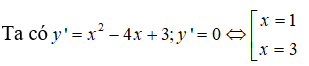500 Bài tập Toán 12 Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số mới nhất
Với 500 Bài tập Toán 12 Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số mới nhất được biên soạn bám sát chương trình Toán lớp 12 giúp bạn học tốt môn Toán hơn.
Mục lục Bài tập Toán 12 Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Bài tập Sự đồng biến nghịch biến của hàm số
Bài tập Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Bài tập Khảo sát sự biến thiên và vẽ đồ thị hàm số
Xem thêm các bài Chuyên đề Toán lớp 12 hay, chi tiết khác:
Chương 2: Hàm số lũy thừa, hàm số mũ, hàm số logarit
Chương 3: Nguyên hàm, tích phân và ứng dụng
Chương 2: Mặt nón, mặt trụ, mặt cầu
-----------------------------------------------------------
Bài tập Sự đồng biến nghịch biến của hàm số - Toán 12
I. Bài tập trắc nghiệm
Bài 1: Cho hàm số y = sin2x - 2x. Hàm số này
A. Luôn đồng biến trên R
B. Chỉ đồng biến trên khoảng (0; +∞)
C. Chỉ nghịch biến trên (-∞; -1)
D. Luôn nghịch biến trên R
Lời giải:
Tập xác định D = R
Ta có : y' = 2.cos2x - 2 = 2(cos2x - 1) ≤ 0; ∀ x
(vì -1 ≤ cos2x ≤ 1)
Vậy hàm số luôn nghịch biến trên R
Chọn đáp án D.
Bài 2: Trong các hàm số sau, hàm số nào chỉ đồng biến trên khoảng (-∞; 1) ?
Lời giải:
Bài 3: Tìm m để hàm số
luôn nghịch biến trên khoảng xác định.
A.-2 < m ≤ 2
B. m < -2 hoặc m > 2
C. -2 < m < 2
D. m ≠ ±2
Lời giải:
Hàm số nghịch biến trên từng khoảng
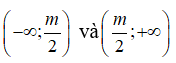
khi và chỉ khi
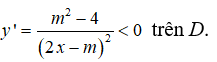
Suy ra m2 - 4 < 0 hay -2 < m < 2. Chọn đáp án C.
Bài 4: Cho hàm số y = -x3 + 3x2 + 3mx - 1, tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng (0; +∞)
A. m < 1
B. m ≥ 1
C. m ≤ -1
D. m ≥ -1
Lời giải:
Ta có y' = -3x2 + 6x + 3m. Hàm số nghịch biến trên khoảng (0; +∞) nếu y' ≤ 0 trên khoảng (o; +∞)
Cách 1: Dùng định lí dấu tam thức bậc hai.
Xét phương trình -3x2 + 6x + 3m. Ta có Δ' = 9(1 + m)
TH1: Δ' ≤ 0 => m ≤ -1 khi đó, -3x2 + 6x + 3m < 0 nên hàm số nghịch biến trên R .
TH2: Δ' > 0 => m > -1; y' = 0 có hai nghiệm phân biệt là x = 1 ±√(1+m) .
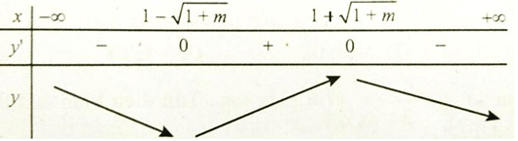
Hàm số nghịch biến trên (0; +∞) <=> 1 + √(1+m) ≤ 0, vô lí.
Từ TH1 và TH2, ta có m ≤ -1
Cách 2: Dùng phương pháp biến thiên hàm số.
Ta có y' = -3x2+ 6x + 3m ≤ 0, ∀x > 0 <=> 3m ≤ 3x2 - 6x, ∀x > 0
Từ đó suy ra 3m ≤ min(3x2 - 6x) với x > 0
Mà 3x2 -6x = 3(x2 -2x + 1) - 3 = 3(x - 1)2 - 3 ≥ -3 ∀ x
Suy ra: min( 3x2 – 6x) = - 3 khi x= 1
Do đó 3m ≤ -3 hay m ≤ -1.
Chọn đáp án C.
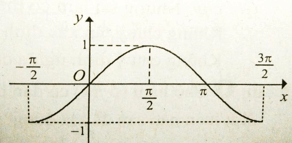
Bài 5: Cho đồ thị hàm số với x ∈ [- π2 ; 3π2] như hình vẽ.
Tìm khoảng đồng biến của hàm số y = sinx với x ∈ [- π2; ]
Lời giải:
Trên khoảng (-) đồ thị hàm số đi lên từ trái sang phải.
Trên khoảng () đồ thị hàm số đi xuống từ trái sang phải.
Do đó hàm số đồng biến trên khoảng (-)
Chọn đáp án A.
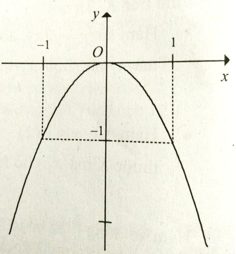
Bài 6: Cho đồ thị hàm số y = -x3 như hình vẽ. Hàm số y = -x3 nghịch biến trên khoảng:
A. (-1;0)
B. (-∞;0)
C. (0;+∞)
D. (-1;1)
Lời giải:
Trên khoảng (0; +∞) đồ thị hàm số đi xuống từ trái sang phải.
Do đó hàm số nghịch biến trên khoảng (0;+∞),
Chọn đáp án C.
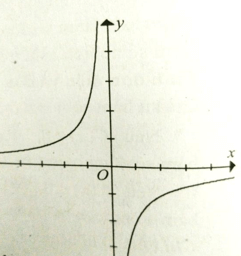
Bài 7: Cho đồ thị hàm số y = - như hình vẽ. Hàm số y = - đồng biến trên
A. (-∞;0)
B. (-∞;0) ∪ (0;+∞)
C. R
D. (-∞;0) và (0;+∞)
Lời giải:
Đồ thị hàm số đi lên từ trái sang phải trên hai khoảng (-∞;0) và (0;+∞)
Chọn đáp án D.
Ghi chú. Những sai lầm có thể gặp trong quá trình làm bài:
- Không chú ý tập xác định nên chọn đáp án C.
- Không chú ý định nghĩa của hàm đồng biến nên chọn đáp án B.
Bài 8: Cho hàm số f(x) có đạo hàm f'(x) = 2
Kết luận nào sau đây là đúng?
A. Hàm số f(x) nghịch biến trên khoảng (-∞;1).
B. Hàm số f(x) đồng biến trên các khoảng (-∞;0) và (1;+∞).
C. Hàm số f(x) đồng biến trên các khoảng và (1;+∞).
D. Hàm số f(x) đồng biến trên các khoảng (1;+∞).
Lời giải:
Điều kiện: x > 0
Bảng xét dấu :
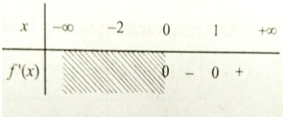
Vậy f(x) đồng biến trên khoảng (1;+∞) và nghịch biến trên khoảng (0;1).
Chọn đáp án D.
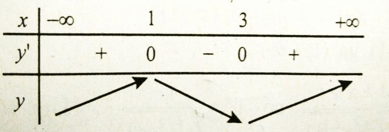
Bài 9: Khoảng nghịch biến của hàm số y = - 2x2 + 3x + 5 là:
A. (1;3)
B.(-∞; 1) ∪ (3; +∞)
C. (-∞; 1) và (3; +∞)
D. (1;+∞)
Lời giải:
Bảng xét dấu y’:
Vậy hàm số nghịch biến trên khoảng (1;3).
Chọn đáp án A.
Bài 10: Cho hàm số y = x4 - 2x2 + 3 . Kết luận nào sau đây đúng?
A. Hàm số nghịch biến trên khoảng (-∞; -1) ∩ (0; 1)
B. Hàm số đồng biến trên khoảng (-1; 0) ∪ (1; +∞)
C. Hàm số nghịch biến trên khoảng (-∞; -1) ∪ (0; 1)
D. Hàm số đồng biến trên các khoảng (-1; 0) và (1; +∞)
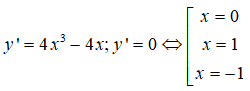
Bảng xét dấu y’:
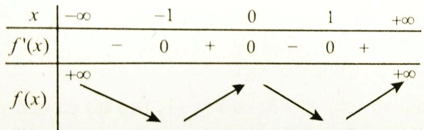
Từ đó ta có: Hàm số đồng biến trên các khoảng (-1; 0) và (1; +∞) , nghịch biến trên các khoảng (-∞; -1) và (0; 1) .
Chọn đáp án D.
Xem thêm các chương trình khác:
- Giải sgk Hóa học 12 (sách mới) | Giải bài tập Hóa 12
- Lý thuyết Hóa học 12
- Giải sbt Hóa học 12
- Các dạng bài tập Hoá học lớp 12
- Giáo án Hóa học lớp 12 mới nhất
- Tóm tắt tác phẩm Ngữ văn 12
- Soạn văn 12 (hay nhất) | Để học tốt Ngữ văn 12 (sách mới)
- Soạn văn 12 (ngắn nhất)
- Tác giả tác phẩm Ngữ văn lớp 12
- Văn mẫu lớp 12
- Giải sgk Sinh học 12 (sách mới) | Giải bài tập Sinh học 12
- Lý thuyết Sinh học 12 | Kiến thức trọng tâm Sinh 12
- Giải sgk Địa Lí 12 (sách mới) | Giải bài tập Địa lí 12
- Lý thuyết Địa Lí 12
- Giải Tập bản đồ Địa Lí 12
- Giải sgk Vật Lí 12 (sách mới) | Giải bài tập Vật lí 12
- Giải sbt Vật Lí 12
- Lý thuyết Vật Lí 12
- Các dạng bài tập Vật lí lớp 12
- Giáo án Vật lí lớp 12 mới nhất
- Giải sgk Lịch sử 12 (sách mới) | Giải bài tập Lịch sử 12
- Giải Tập bản đồ Lịch sử 12
- Lý thuyết Lịch sử 12
- Giải sgk Giáo dục công dân 12
- Lý thuyết Giáo dục công dân 12
- Giải sgk Giáo dục quốc phòng - an ninh 12 (sách mới) | Giải bài tập GDQP 12
- Lý thuyết Giáo dục quốc phòng 12 | Kiến thức trọng tâm GDQP 12
- Lý thuyết Tin học 12
- Lý thuyết Công nghệ 12