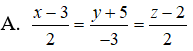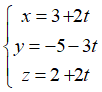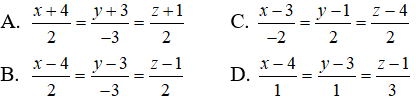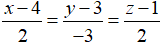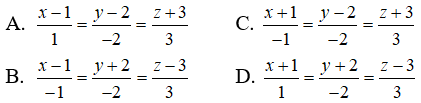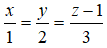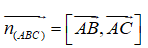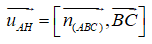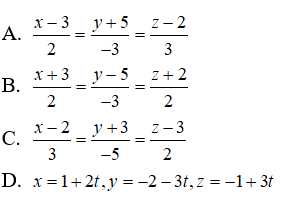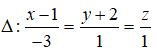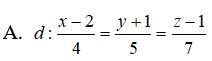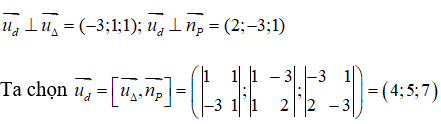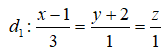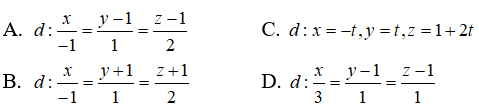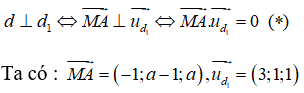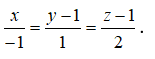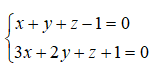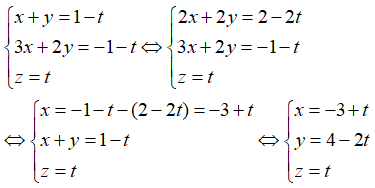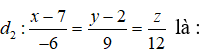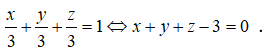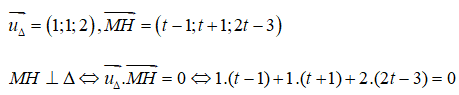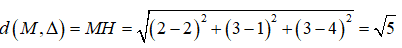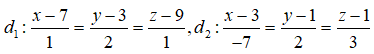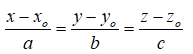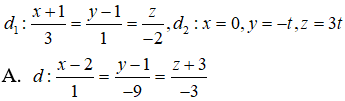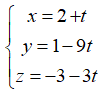50 Bài tập Phương trình đường thẳng Toán 12 mới nhất
Với Bài tập Phương trình đường thẳng Toán lớp 12 mới nhất được biên soạn bám sát chương trình Toán 12 giúp các bạn học tốt môn Toán hơn.
Tài liệu gồm: 15 bài tập trắc nghiệm, 15 bài tập tự luận có lời giải và 20 bài tập vận dụng. Mời các bạn đón xem:
Bài tập Phương trình đường thẳng - Toán 12
I. Bài tập trắc nghiệm
Câu 1: Trong không gian Oxyz, cho hai điểm A(1; -2; 0), B(3; -5; 2) . Phương trình tham số của đường thẳng AB là:
B. x = 2 + 3t, y = -3 - 5t, z = 2 + 2t
C. x = 3 + 2t, y = -5 - 3t, z = 2 + 2t
D. x = 1 + 2t, y = -2 + 3t, z = 2t
Lời giải:
Đường thẳng AB đi qua B(3; -5; 2) và VTCP (2; -3; 2) có phương trình tham số là:
Câu 2: Trong không gian Oxyz, cho đường thẳng d đi qua M(4;3;1) và song song với đường thẳng Δ: x = 1 + 2t, y = 1 - 3t, z = 3 + 2t. Phương trình chính tắc của đường thẳng d là:
Lời giải:
Đường thẳng ∆ có vecto chỉ phương (2; -3; 2)
Đường thẳng d đi qua M(4;3;1) và song song với đường thẳng ∆ nên có vecto chỉ phương là (2; -3; 2). Phương trình chính tắc của đường thẳng d là:
Câu 3: Trong không gian Oxyz, phương trình chính tắc của đường thẳng d đi qua điểm M(-1;-2;3) và vuông góc với mặt phẳng (P): x - 2y + 3z - 1 = 0
Mặt phẳng (P) có vecto pháp tuyến (1; -2; 3) là:
Vì đường thẳng d đi qua điểm M(-1;-2;3) và vuông góc với mặt phẳng (P) nên có vecto chỉ phương là = (1; -2; 3) . Phương trình chính tắc của d:
Câu 4: Trong không gian Oxyz, cho d là đường thẳng đi qua điểm M(1;2;3) và vuông góc với mặt phẳng (Oxy). Trong những khẳng định dưới đây, khẳng định nào sai?
A. Phương trình chính tắc của đường thẳng d là:
B. Đường thẳng d có một vectơ chỉ phương là = (0; 0; 1)
C. Đường thẳng d nằm trong hai mặt phẳng: (P): x - 1 = 0, (Q): y - 2 = 0
D. Phương trình tham số của đường thẳng d là: x = 1, y = 2, z = 1
Vì đường thẳng d vuông góc với mặt phẳng (Oxy) nên đường thẳng d có vectơ chỉ phương là (0 ;0 ;1). Từ đó suy ra A là khẳng định sai.
Câu 5: Cho tam giác ABC có A(1; -2; 3), B(0; 5; 6), C(1; 3; 2). Gọi H là hình chiếu vuông góc của A trên đường thẳng BC. Trong những khẳng định dưới đây, khẳng định nào sai?
A. Một vectơ pháp tuyến của mặt phẳng (ABC) là:
B. Một vectơ chỉ phương của đường thẳng AH là:
C. AH ⊥ BC
D. Các khẳng định trên không đồng thời đúng
Lời giải:
Ta có thể thấy ngay rằng các khẳng định A và C đều đúng.
Ta có
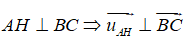
Mặt khác ta có
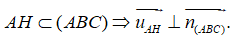
Từ đó ta suy ra
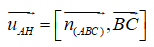
là một vectơ chỉ phương của đường thẳng AH.
Vậy D là khẳng định sai.
Câu 6: Trong không gian Oxyz, cho hai điểm A(1; -2; -1), B(3; -5; 2) . Phương trình chính tắc của đường thẳng AB là:
Lời giải:
Đường thẳng AB đi qua điểm B(3;-5;2) và có vectơ chỉ phương là . Vậy phương trình chính tắc của đường thẳng AB là:
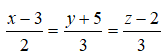
Câu 7: Trong không gian Oxyz, lập phương trình tham số của đường thẳng d đi qua điểm M(2;-1;1), vuông góc với đường thẳng
và song song với mặt phẳng (P): 2x - 3y + z - 2 = 0.
B. d: x = 2 + 4t, y = 1 + 5t, z = 1 + 7t
C. d: x = 2 +4t, y = -1 - 5t. z = 1 + 7i
D. d: x = -2 + 4t, y = 1 + 5t, z = -1 + 7t
Lời giải:
Từ giả thiết suy ra
Mặt khác đường thẳng d đi qua điểm M(2;-1;1) nên phương trình tham số của đường thẳng d là: x = 2+ 4t, y = -1, + 5t, z = 1 + 7t .
Vậy đáp án đúng là B
Câu 8: Trong không gian Oxyz, lập phương trình chính tắc của đường thẳng d đi qua điểm M(0;1;1) , vuông góc với đường thẳng
và cắt đường thẳng d2: x = -1, y = t, z = 1 + t
Lời giải:
Gọi A = d ∩ d2 . Ta có A ∈ d2 => A(-1; a; a+ 1).
Theo giả thiết:
Thay vào (*) ta được :
-1.3 + (a - 1).1 + a.1 = 0 <=> 2a - 4 = 0 <=> a = 2 <=> = = (-1; 1; 2)
Vậy phương trình chính tắc của đường thẳng d là :
Vậy đáp án đúng là A.
Câu 9: Trong không gian Oxyz, lập phương trình tham số của đường thẳng d là giao tuyến của hai mặt phẳng cắt nhau : (P): x + y + z - 1 = 0, (Q): 3x + 2y + z + 1 = 0
A. d: x = -3 + t, y = 4 + 2t, z = t
B. d: x = -3 + t, y = 4 - 2t, z = t
C. d: x = -3 + t, y = 4 - 2t, z =1 + t
D. d: x =1 - 3t, y = -1 + 4t, z = t
Tọa độ các điểm thuộc d là nghiệm của hệ phương trình :
Đặt z=t, thay vào hệ trên ta được :
Vậy đáp án đúng là B.
Câu 10: Trong không gian Oxyz, vị trí tương đối của hai đường thẳng
d1: x = 2 + 4t, y = -6t, z = -1-8t và
A. Cắt nhau
B. song song
C. chéo nhau
D. trùng nhau
Đường thẳng d1 đi qua điểm M1(2; 0; -1) và có vectơ chỉ phương là = (4; -6; -8) ;
đường thẳng d2 đi qua điểm M2(7; 2; 0) và có vectơ chỉ phương là = (-6; 9; 12) .
Do hai vectơ và cùng phương nên các đáp án A và C là sai.
Thay tọa độ điểm M1 vào d2 , ta thấy :
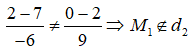
Do đó hai đường thẳng d1 và d2 song song.
Vậy đáp án B là đúng
II. Bài tập tự luận có lời giải
Câu 1: Trong không gian Oxyz, cho ba điểm A(3;0;0), B(0;3;0), C(0;0;3). Trong những khẳng định dưới đây, khẳng định nào sai?
- Phương trình của mặt phẳng (ABC) là: x + y + z - 3 = 0
- Hình chóp O.ABC là hình chóp tam giác đều
- Phương trình đường thẳng qua O, vuông góc với mặt phẳng (ABC) là: x = t, y = t, z = t
- Khoảng cách từ O đến mặt phẳng ABC bằng 3
Lời giải:
Phương trình mặt phẳng (ABC) là:
Từ đó suy ra khoảng cách từ O đến mặt phẳng (ABC) là:
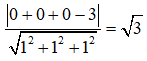
Câu 2: Trong không gian Oxyz, cho đường thẳng Δ: x = 1 + 2, y = 2 + t, z = 1 + 2t và điểm M(2; 1; 4). Khoảng cách từ M đến đường thẳng Δ là?
Lời giải:
Cách 1. Gọi H là hình chiếu vuông góc của M trên đường thẳng Δ.
Ta có: H ∈ Δ => H(1 + t; 2 + t; 1 + 2t)
<=> 6t - 6 = 0 <=> t = 1 => H(2; 3; 3)
Vậy khoảng cách từ M đến đường thẳng Δ là:
Vậy đáp án đúng là C
Cách 2. Δ đi qua điểm A(1 ;2 ;1) và có vectơ chỉ phương là
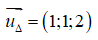
Ta có:
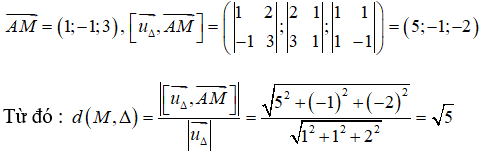
Câu 3: Trong không gian Oxyz, cho hai đường thẳng chéo nhau :
Cho mặt cầu (S) có một đường kính là đoạn vuông góc chung của hai đường thẳng đã cho. Bán kính của mặt cầu (S) là?
Lời giải:
Ta có d1 đi qua điểm M1(7; 3; 9) và có vectơ chỉ phương là = (1; 2; 1); d2 đi qua điểm M2(3; 1; 1) và có vectơ chỉ phương là .
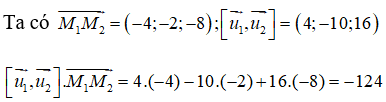
Bán kính của mặt cầu (S) là :
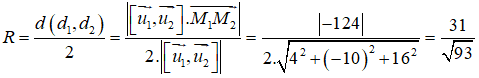
Câu 4: Cho tam giác ABC có ABC có A(2; 2; 1), B(4; 4; 2), C(-2; 4; -3) . Vectơ nào dưới đây là vectơ chỉ phương của đường phân giác trong AD của tam giác ABC.
Lời giải:
Ta có:
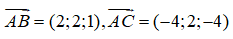
Từ điểm D kẻ đường thẳng song song với AC, cắt cạnh AB tại điểm E. Từ D kẻ đường thẳng song song với AB cắt cạnh AC tại F. Do AD là đường phân giác trong của tam giác ABC nên ta suy ra AEDF là hình thoi.
Đặt AE=AF=k. Ta có:
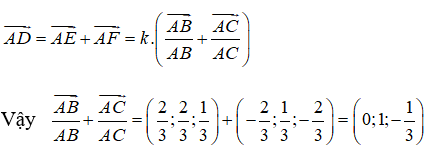
là một vectơ chỉ phương của đường thẳng AD. Từ đó suy ra C là khẳng định đúng.
Ta cũng lưu ý rằng khẳng định A sai, do tam giác ABC không cân tại đỉnh A.
Câu 5: Trong không gian Oxyz, cho d là đường thẳng đi qua điểm M0(x0; y0; z0) và có vectơ chỉ phương là , với a, b, c khác 0. Trong các khẳng định sau, khẳng định nào sai?
- Phương trình chính tắc của đường thẳng d là:
- Phương trình tham số của đường thẳng d là: x = x0 + at, y = y0 + bt, z = z0 + at
- Đường thẳng d nằm trong hai mặt phẳng :(P): b(x - x0) - a(y - y0) = 0 và (Q): c(x - x0) - a(z - z0) = 0
- Phương trình đường thẳng d là: a(x - x0) + b (y - y0) + c(z - z0) = 0
Câu 6: Tìm tất cả các giá trị của a để hai đường thẳng sau chéo nhau :
d1: x = 1 + at, y = t, z = -1 + 2t, d2: x = 1 - t', y = 2 + 2t', z = 3 - t'
Lời giải:
Hai đường thẳng d1, d2 lần lượt đi qua hai điểm M1(1; 0; -1), M2(1; 2; 3) và có vectơ chỉ phương lần lượt là
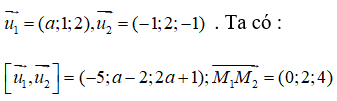
Hai đường thẳng chéo nhau khi và chỉ khi :
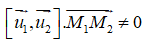
⇔ -5.0 + (a - 2).2 + (2a + 1).4 ≠ 0 ⇔ 10a ≠ 0 ⇔ a ≠ 0
Câu 7: Tìm tất cả các giá trị của a để hai đường thẳng sau vuông góc
d1: x = 1 - t, y = 1 + 2t, z = 3 + at, d2: x = a + at, y = -1 + t, z = -2 + 2t
Lời giải:
Hai đường thẳng đã cho có hai vecto chỉ phương là (-1; 2; a); (a; 1; 2)
Để hai đường thẳng sau vuông góc thì
= -1.a + 2.1 + a.2 = 0 ⇔ a + 2 = 0 ⇔ a = -2
Câu 8: Vị trí tương đối của đường thẳng d: x = 1 + 2t, y = 1 - t, z = 1 - t và mặt phẳng (P): x + y + z - 3 = 0 là?
Lời giải:
Đường thẳng d đi qua điểm A( 1 ; 1 ;1) ; có một vecto chỉ phương là ( 2 ; -1 ; -1)
Mặt phẳng (P) có vecto pháp tuyến là
Ta có: = 2.1 + (-1).1 + (-1).1 = 0 và A ∈ (P)
Suy ra, đường thẳng d thuộc mặt phẳng (P).
Câu 9: Vị trí tương đối của đường thẳng d: x = 2 + 4t, y = 3 + t, z = -5t và mặt phẳng (P): x + y + z - 3 = 0 là?
Lời giải:
Đường thẳng d đi qua điểm M(2 ;3 ;0) và có vectơ chỉ phương là = (4; 1; -5), mặt phẳng (P) có vectơ pháp tuyến là = (1; 1; 1). Ta có :
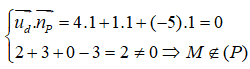
Suy ra đường thẳng d song song với mặt phẳng (P).
Câu 10: Trong không gian Oxyz, lập phương trình tham số của đường thẳng d đi qua điểm M(2;1;-3) và vuông góc với hai đường thẳng:
Lời giải:
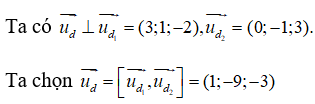
Mặt khác d đi qua điểm M(2 ;1 ;-3).
Vậy phương trình tham số của đường thẳng d là:
x = 2 + t, y = 1 - 9t, z = -3 - 3t
III. Bài tập vận dụng
Bài 1 Trong không gian Oxyz, cho hai điểm A(-2; -2; -4), M(1; 0; 0) . Lập phương trình đường thẳng d đi qua điểm M, nằm trong mặt phẳng (P): x + y + z - 1 = 0 sao cho khoảng cách từ A đến đường thẳng d đạt giá trị lớn nhất
Bài 2 Trong không gian Oxyz, lập phương trình tham số của đường thẳng d đi qua điểm A(-2;3;1), vuông góc với trục Ox, đông thời d song song với mặt phẳng: (P): x + 2y - 3z = 0
Bài 3 Trong không gian Oxyz, lập phương trình chính tắc của đường thẳng d đi qua điểm M(0;1;-1), nằm trong mặt phẳng (P): x + 2y + z - 1 = 0 và vuông góc với đường thẳng
Bài 4 Trong không gian Oxyz, lập phương trình tham số của đường thẳng d là giao tuyến của hai mặt phẳng cắt nhau: (P): x + 2y - z + 1 = 0, (Q): x + y + 2z + 3 = 0
Bài 5 Trong không gian Oxyz, cho đường thẳng d là giao tuyến của hai mặt phẳng cắt nhau (P): x + y - z + 3 = 0, (Q): 2x - y + 6z - 2 = 0. phương trình chính tắc của đường thẳng d là?
Bài 6 Trong không gian Oxyz, lập phương trình chính tắc của đường thẳng d đi qua điểm M(0;1;-1), vuông góc và cắt đường thẳng Δ: x = 1 - 4t, y = t, z = -1 + 4t
Bài 7 Trong không gian Oxyz, cho hai điểm A(2; 0; 1), B(8; 4; -5) và mặt phẳng 2x + 2y - z + 1 = 0 . Tìm tọa độ của điểm M thuộc mặt phẳng (P) sao cho AM2 + BM2 đạt giá trị nhỏ nhất
Bài 8 Trong không gian Oxyz, cho mặt cầu (S) có phương trình là: (x + 1)2 + (y - 4)2 + (z + 3)2 = 36 . Số mặt phẳng (P) chứa trục Ox và tiếp xúc với mặt cầu (S) là?
Bài 9 Cho đường thẳng d: x = 1 + t, y = 2 - t, z = 1 + at và mặt phẳng (P): 2x + y + z + b = 0 . Tìm a và b để đường thẳng d nằm trong mặt phẳng (P)
Bài 10 Trong không gian Oxyz, tọa độ của hình chiếu vuông góc của điểm M(5;2;3) trên mặt phẳng (P): 2x + 2y - z + 1 = 0 là?
Xem thêm các bài Bài tập Toán lớp 12 hay, chi tiết khác:
Bài tập Phương trình mặt phẳng
Xem thêm các chương trình khác:
- Giải sgk Hóa học 12 (sách mới) | Giải bài tập Hóa 12
- Lý thuyết Hóa học 12
- Giải sbt Hóa học 12
- Các dạng bài tập Hoá học lớp 12
- Giáo án Hóa học lớp 12 mới nhất
- Tóm tắt tác phẩm Ngữ văn 12
- Soạn văn 12 (hay nhất) | Để học tốt Ngữ văn 12 (sách mới)
- Soạn văn 12 (ngắn nhất)
- Tác giả tác phẩm Ngữ văn lớp 12
- Văn mẫu lớp 12
- Giải sgk Sinh học 12 (sách mới) | Giải bài tập Sinh học 12
- Lý thuyết Sinh học 12 | Kiến thức trọng tâm Sinh 12
- Giải sgk Địa Lí 12 (sách mới) | Giải bài tập Địa lí 12
- Lý thuyết Địa Lí 12
- Giải Tập bản đồ Địa Lí 12
- Giải sgk Vật Lí 12 (sách mới) | Giải bài tập Vật lí 12
- Giải sbt Vật Lí 12
- Lý thuyết Vật Lí 12
- Các dạng bài tập Vật lí lớp 12
- Giáo án Vật lí lớp 12 mới nhất
- Giải sgk Lịch sử 12 (sách mới) | Giải bài tập Lịch sử 12
- Giải Tập bản đồ Lịch sử 12
- Lý thuyết Lịch sử 12
- Giải sgk Giáo dục công dân 12
- Lý thuyết Giáo dục công dân 12
- Giải sgk Giáo dục quốc phòng - an ninh 12 (sách mới) | Giải bài tập GDQP 12
- Lý thuyết Giáo dục quốc phòng 12 | Kiến thức trọng tâm GDQP 12
- Lý thuyết Tin học 12
- Lý thuyết Công nghệ 12