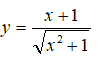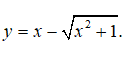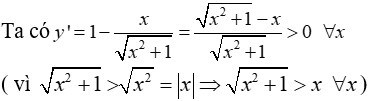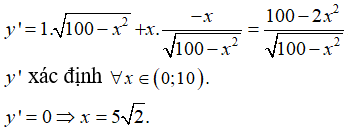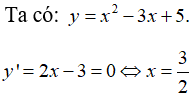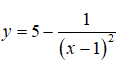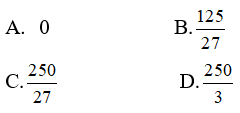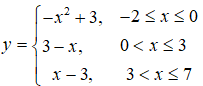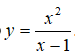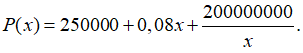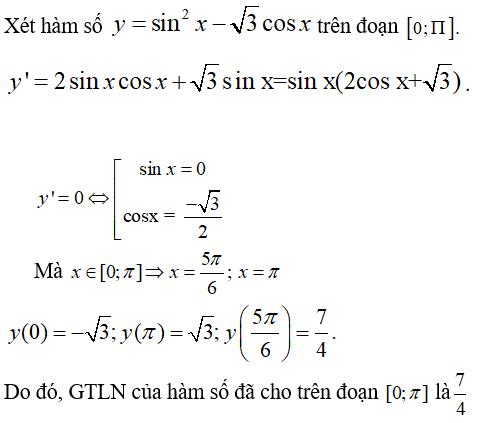50 Bài tập Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 mới nhất
Với 50 Bài tập Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán lớp 12 mới nhất được biên soạn bám sát chương trình Toán 12 giúp các bạn học tốt môn Toán hơn.
Tài liệu gồm: 15 bài tập trắc nghiệm, 15 bài tập tự luận có lời giải và 20 bài tập vận dụng. Mời các bạn đón xem:
Bài tập Giá trị lớn nhất và giá trị nhỏ nhất của hàm số - Toán 12
I. Bài tập trắc nghiệm
Bài 1: GTLN của hàm số
trên khoảng (0; 4) đạt được
A. x = 1
B. x = -1
C. x =
D. Không tồn tại
Xét
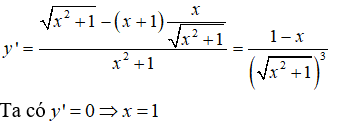
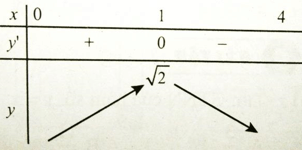
Ta có y' = 0 => x = 1
Vậy hàm số có GTLN bằng khi x = 1.
Chọn đáp án A.
Bài 2: Tìm GTLN của hàm số
A. 0
B. +∞
C. Không tồn tại
D. Không có đáp án
Lời giải:
Tập xác định R.
Ta có bảng biến thiên:
Hàm số không có GTLN trên R . Chọn đáp án C.
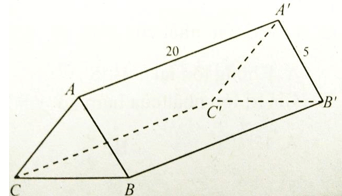
Bài 3: Một hành lang giữa hai tòa tháp có hình dạng một hình lăng trụ đứng. Hai mặt bên ABB’A’ và ACC’A’ là hai tấm kính hình chữ nhật dài 20m, rộng 5m. Với độ dài xấp xỉ nào của BC thì thể tích hành lang này lớn nhất
A. 6m
B. 7m
C. 8m
D. 9m.
Lời giải:
Thể tích hình lăng lớn nhất khi và chỉ khi diện tích ΔABC lớn nhất.
Gọi độ dài BC là x (m). Kẻ AH ⊥ BC.
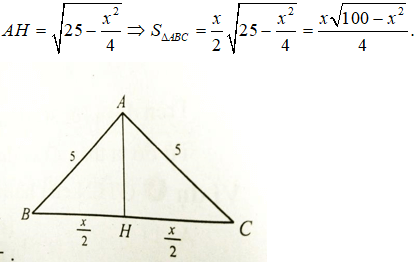
Bài toán đưa về tìm x ∈ (0; 10) để hàm số y = x có giá trị lớn nhất.
Ta có:
Bảng biến thiên:
Hàm số đạt giá trị lớn nhất tại x = 5 ≈ 7. Chọn đáp án B.
Bài 4: Tìm GTNN của hàm số y = x2 - 3x + 5
A.
B.
C. 3
D. 5
Lời giải:
Lập bảng biến thiên ta được, hàm số đạt giá trị nhỏ nhất tại:
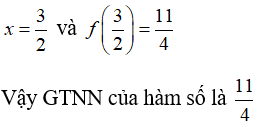
Bài 5: Giá trị lớn nhất của hàm số f(x) = -x2 + 4 là:
A. 0
B. 4
C.2
D. Không có đáp án.
Tập xác định: D = R. Ta có
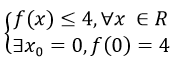
Do đó giá trị lớn nhất của hàm số f(x) là 4 đạt được khi x = 0. Chọn đáp án B.
Bài 6: Giá trị lớn nhất của hàm số
đạt được khi x nhận giá trị bằng:
A. 1
B. 5
C. 0
D. Không có đáp án.
Tập xác định: D = R \ {1}
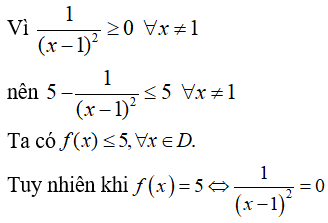
=> không tồn tại x thỏa mãn. Do đó hàm số không có giá trị lớn nhất. Chọn đáp án D.
Bài 7: Giá trị lớn nhất của hàm số y = x(5 - 2x)2 trên [0; 3] là:
Lời giải:
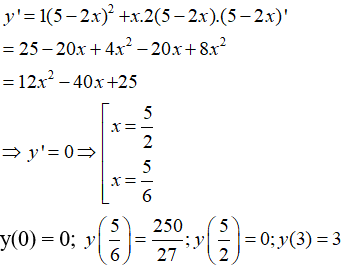
Vậy GTLN của hàm số trên [0; 3] là đạt được khi x = .
Chọn đáp án C.
Bài 8: Giá trị lớn nhất của hàm số
có đồ thị như hình bên là
A. 3
B. 7
B. -1
D. 4
Chọn đáp án D.
Chú ý. Cần phân biệt giá trị lớn nhất của hàm số và cực đại của hàm số.
Bài 9: Một công ti quản lí chuẩn bị xây dựng một khu chung cư mới. Họ tính toán nếu tòa nhà có x căn hộ thì chi phí bảo trì của tòa nhà là: C(x) = 4000 - 14x + 0,04x2. Khu đất của họ có thể xây được tòa nhà chứa tối đa 300 căn hộ. Hỏi họ nên xây dựng tòa nhà có bao nhiêu căn hộ để chi phí bảo trì của tòa nhà là nhỏ nhất?
A. 150
B.175
C. 300
D.225
Ta có x là số căn hộ. Rõ ràng x phải thỏa mãn điều kiện 0 ≤ x ≤ 300. Chi phí bảo trì tòa nhà C(x) = 4000 - 14x + 0,04x2
Ta phải tìm 0 ≤ xo ≤ 300 sao cho C(xo) có giá trị nhỏ nhất.
Ta có C'(x) = -14 + 0,08x, 0 ≤ x ≤ 300. C'(x) = 0 <=> x = 175
Trên đoạn [0; 300] ta có C(0) = 4000; C(175) = 2775; C(300) = 3400
Từ đó ta thấy C(x) đạt giá trị nhỏ nhất khi x = 175. Chọn đáp án B.
Bài 10: GTLN của hàm số y = -x2 + 4x + 7 đạt được khi x bằng:
A. 11
B. 4
C. 7
D. 2
y' = -2x + 4 = 0 <=> x = 2
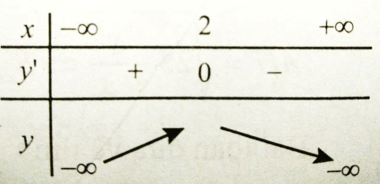
Dựa vào bảng biến thiên; GTLN của hàm số là 11 khi x= 2.
Chú ý. Cần phân biệt GTLN của hàm số (max y) với giá trị x để hàm số đạt được GTLN.
II. Bài tập tự luận có lời giải
Bài 1: GTLN của hàm số y = 2sinx + cos2x trên đoạn [0; π] là?
Lời giải:
Xét hàm số y=2sin x + cos 2x trên đoạn
y’=2cos x- 2sin 2x = 2cos x(1- 2sin x)
Trên đoạn [0; π]
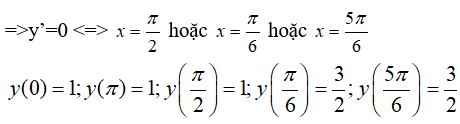
Giá trị lớn nhất của hàm số này trên [0; π] là y = .
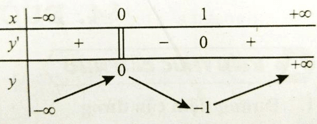
Bài 2: Cho hàm số y = f(x) xác định và liên tục trên R và có bảng biến thiên. Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có đúng một cực trị.
B. Hàm số có giá trị cực tiểu bằng 1.
C. Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng -1.
D. Hàm số đạt cực đại tại x = 0 và cực tiểu tại x = 1
Dựa vào định nghĩa, hàm số không tồn tại giá trị lớn nhất và giá trị nhỏ nhất. Hàm số đạt cực đại tại x=0 và cực tiểu tại x=1.
Bài 3: Xét hàm số
Trong các khẳng định sau, khẳng định nào là đúng?
A. Hàm số có giá trị lớn nhất bằng 4.
B. Hàm số có giá trị cực đại bằng 4
C. Hàm số có giá trị lớn nhất bằng 0.
D. Hàm số có giá trị cực đại bằng 0
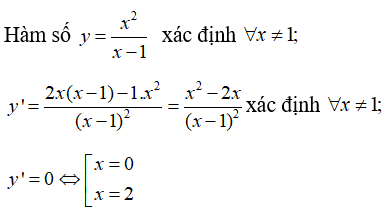
Bảng biến thiên
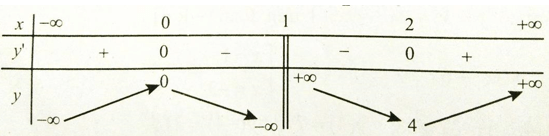
Hàm số không tồn tại giá trị lớn nhất. Hàm số có giá trị cực đại bằng 0.
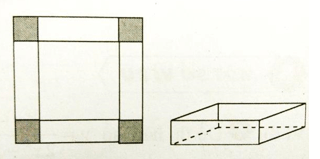
Bài 4: Cho tấm nhôm hình vuông cạnh 12cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x (cm), rồi gập tấm nhôm lại như hình vẽ bên để được một cái hộp không nắp. Với giá trị nào của x thì hộp nhận được có thể tích lớn nhất?
Lời giải:
Hình hộp có đáy là hình vuông cạnh: 12 - 2x
Chiều cao của hình hộp là: x
Thể tích hình hộp là y = x(12 - 2x)2
Bài toán đưa về tìm x ∈ (0; 6) để hàm số y = f(x) = x(12 - 2x)2 có giá trị lớn nhất.
y' = 1(12 - 2x)2 + x.2.(12 - 2x).(-2)
12x2 - 96x + 144;
y' xác định ∀ x ∈ (0; 6)
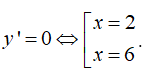
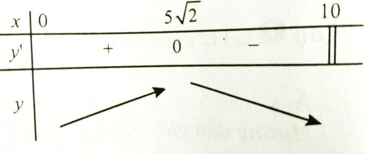
Bảng biến thiên
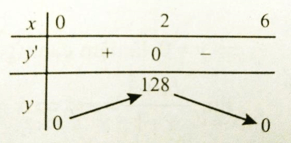
Hàm số đạt giá trị lớn nhất tại x=2
Bài 5: Khu chung cư Royal City có 250 căn hộ cho thuê. Nếu người ta cho thuê x căn hộ thì lợi nhuận hàng tháng, tính theo triệu đồng, được cho bởi:
P(x) = -8x2 + 3200x - 80000. Hỏi lợi nhuận tối đa họ có thể đạt được là bao nhiêu?
Lời giải:
Ta có x ∈ (0; 250) ,P’(x) = -16x+3200.
Khi đó P’(x)=0 ⇔ -16x + 3200 = 0 ⇔ x = 200 (loại).
P(0)= - 8000; P(250) = 292 000
Do đó lợi nhuận tối đa họ thu được là P(250)=292000.
Bài 6: Một nhà máy sản xuất được 60000 sản phẩm trong một ngày và tổng chi phí sản xuất x sản phẩm được cho bởi:
Hỏi nhà máy nên sản xuất bao nhiêu sản phẩm mỗi ngày để chi phí sản xuất là nhỏ nhất?
Lời giải:
Ta có x ∈ (0; 60000)
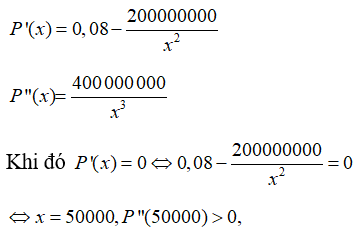
Do đó, hàm số đạt cực tiểu tại x = 50000.
Nên x=50000 là số sản phẩm cần sản xuất mỗi ngày để tối thiểu chi phí.
Bài 17: GTLN của hàm số y = sin2x - cosx trên đoạn [0; π] là?
Lời giải:
Bài 18: GTNN của hàm số y = x3 + 3x2 - 9x + 1 trên đoạn [-4;4] là?
Lời giải:
Xét hàm số y = x3 + 3x2 - 9x + 1 trên đoạn [-4;4].
Ta có:
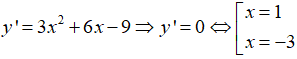
y(1) = -4, y(-3) = 28; y(4) = 77; y(-4) = 21
GTNN của hàm số y = X3 - 9x + 1 trên đoạn [-4;4] là -4 khi x= 1
Bài 9: GTLN của hàm số y = x4 - 8x2 + 16 trên đoạn [-1;3] là?
Lời giải:
Xét hàm số y = x4 - 8x2 + 16 trên đoạn [-1;3]
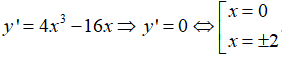
y(0) = 16, y(2) = 0; y(-1) = 9; y(3) = 25
GTLN của hàm số y = x4 - 8x + 16 trên đoạn [-1;3] là 25 khi x = 3.
Bài 10: GTNN của hàm số y = trên nửa khoảng (-2;4] là
Lời giải:
Xét hàm số
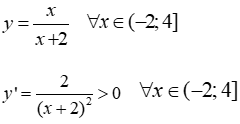
Ta có bảng biến thiên
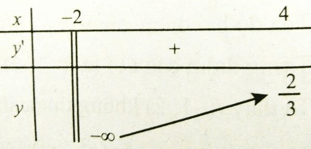
Hàm số không có GTNN
III. Bài tập vận dụng
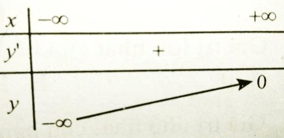
Bài 1 GTNN của hàm số y = x + 2 + trên khoảng (1; +∞) là?
Bài 2 Xét tính đồng biến, nghịch biến và tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) y = x2 trên đoạn [-3; 0];
b) y = trên đoạn [3; 5].
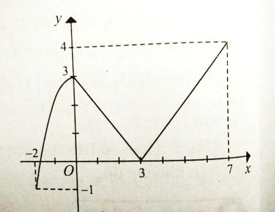
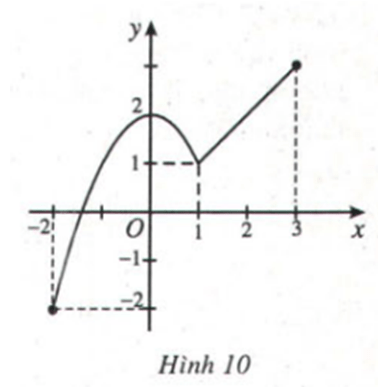
Bài 3 Cho hàm số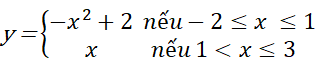
có đồ thị như Hình 10. Hãy chỉ ra giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [-2; 3] và nêu cách tính.
Bài 4 Lập bảng biến thiên của hàm số f(x) = . Từ đó suy ra giá trị nhỏ nhất của f(x) trên tập xác định.
Bài 5 Tính giá trị lớn nhất và nhỏ nhất của hàm số:
a) y = x3 - 3x2 - 9x + 35 trên các đoạn [-4; 4] và [0; 5] ;
b) y = x4 - 3x2 + 2 trên các đoạn [0; 3] và [2; 5] ;
c)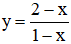 
trên các đoạn [2 ; 4] và [-3 ; -2] ;
d)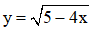 
trên đoạn [-1 ; 1].
Bài 6 Trong số các hình chữ nhật có cùng chu vi 16cm, hãy tìm hình chữ nhật có diện tích lớn nhất.
Bài 7 Trong tất cả các hình chữ nhật có diện tích 48 m2, hãy xác định hình chữ nhật có chu vi nhỏ nhất.
Bài 8 Tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số
a) trên các đoạn và ;
b) trên các đoạn và ;
c) trên các đoạn và ;
d) trên đoạn .
Bài 9 Trong các hình chữ nhật có cùng chu vi 16 cm, hãy tìm hình chữ nhật có diện tích lớn nhất.
Bài 10 Trong tất cả các hình chữ nhật cùng có diện tích 48m2, hãy xác định hình chữ nhật có chu vi nhỏ nhất.
Xem thêm các bài Bài tập Toán lớp 12 hay, chi tiết khác:
Bài tập Sự đồng biến nghịch biến của hàm số
Xem thêm các chương trình khác:
- Giải sgk Hóa học 12 (sách mới) | Giải bài tập Hóa 12
- Lý thuyết Hóa học 12
- Giải sbt Hóa học 12
- Các dạng bài tập Hoá học lớp 12
- Giáo án Hóa học lớp 12 mới nhất
- Tóm tắt tác phẩm Ngữ văn 12
- Soạn văn 12 (hay nhất) | Để học tốt Ngữ văn 12 (sách mới)
- Soạn văn 12 (ngắn nhất)
- Tác giả tác phẩm Ngữ văn lớp 12
- Văn mẫu lớp 12
- Giải sgk Sinh học 12 (sách mới) | Giải bài tập Sinh học 12
- Lý thuyết Sinh học 12 | Kiến thức trọng tâm Sinh 12
- Giải sgk Địa Lí 12 (sách mới) | Giải bài tập Địa lí 12
- Lý thuyết Địa Lí 12
- Giải Tập bản đồ Địa Lí 12
- Giải sgk Vật Lí 12 (sách mới) | Giải bài tập Vật lí 12
- Giải sbt Vật Lí 12
- Lý thuyết Vật Lí 12
- Các dạng bài tập Vật lí lớp 12
- Giáo án Vật lí lớp 12 mới nhất
- Giải sgk Lịch sử 12 (sách mới) | Giải bài tập Lịch sử 12
- Giải Tập bản đồ Lịch sử 12
- Lý thuyết Lịch sử 12
- Giải sgk Giáo dục công dân 12
- Lý thuyết Giáo dục công dân 12
- Giải sgk Giáo dục quốc phòng - an ninh 12 (sách mới) | Giải bài tập GDQP 12
- Lý thuyết Giáo dục quốc phòng 12 | Kiến thức trọng tâm GDQP 12
- Lý thuyết Tin học 12
- Lý thuyết Công nghệ 12