Lý thuyết Tam giác cân. Đường trung trực của đoạn thẳng – Toán lớp 7 Kết nối tri thức
Với lý thuyết Toán lớp 7 Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sách Kết nối tri thức sẽ giúp học sinh nắm vững kiến thức trọng tâm để học tốt môn Toán 7.
A. Lý thuyết Toán 7 Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng - Kết nối tri thức
1. Tam giác cân và tính chất
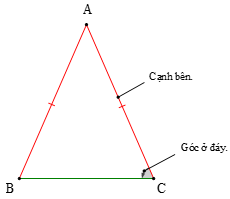
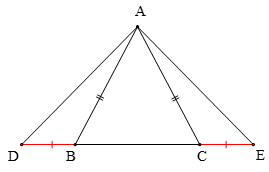
• Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau.
Ví dụ: Trong hình dưới đây, có cạnh AB = AC được gọi là tam giác cân tại đỉnh A, hai cạnh AB và AC là hai cạnh bên, BC là cạnh đáy, và là hai góc ở đáy, là góc ở đỉnh.
• Tính chất:
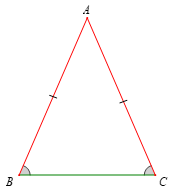
+ Trong tam giác cân, hai góc ở đáy bằng nhau.
+ Tam giác có hai góc ở đáy bằng nhau thì tam giác đó là tam giác cân.
Ví dụ: Tam giác ABC cân tại A thì =. Ngược lại, tam giác ABC có =thì tam giác ABC cân tại A.
Chú ý:
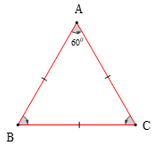
• Tam giác đều là tam giác có ba cạnh bằng nhau. Khi đó ba góc cũng bằng nhau và bằng 60°.
Ví dụ: Tam giác ABC có AB = AC = BC thì tam giác ABC được gọi là tam giác đều. Tam giác ABC đều có = == 60°.
• Một tam giác có ba cạnh hoặc ba góc bằng nhau thì tam giác ấy là tam giác đều.
• Tam giác cân có 1 góc bằng 60° thì tam giác ấy là tam giác đều.
2. Đường trung trực của một đoạn thẳng
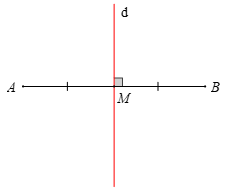
• Định nghĩa: Đường thẳng vuông góc với đoạn thẳng tại trung điểm của nó được gọi là đường trung trực của đoạn thẳng đó.
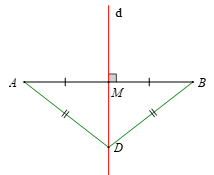
Ví dụ: Đường thẳng d vuông góc với đoạn AB tại M và M là trung điểm của AB. Khi đó d được gọi là đường trung trực của đoạn thẳng AB.
• Đường trung trực của đoạn thẳng cũng là trục đối xứng của đoạn thẳng đó.
• Tính chất: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
Ví dụ: Đường thẳng d là đường trung trực của đoạn thẳng AB và D ∈ d.
Khi đó DA = DB.
• Đường trung trực của đoạn thẳng là tập hợp tất cả các điểm cách đều hai mút của đoạn thẳng đó.
Chú ý:
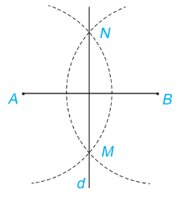
• Cách vẽ đường trung trực của đoạn thẳng bằng compa và thước thẳng.
Chẳng hạn: Vẽ đường thẳng d là đường trung trực của đoạn thẳng AB như sau:
+ Vẽ đoạn thẳng AB;
+ Lấy A làm tâm, vẽ cung tròn (bán kính lớn hơn ). Sau đó lấy B làm tâm, vẽ cung tròn cùng bán kính sao cho hai cung này cắt nhau tại hai điểm M và N;
+ Dùng thước thẳng vẽ đường thẳng đi qua M và N. Đường thẳng đó là đường trung trực của đoạn thẳng AB.
Bài tập Tam giác cân. Đường trung trực của đoạn thẳng
Bài 1. Cho tam giác ABC cân tại A. Kẻ BH và CK lần lượt vuông góc với AC và AB (H ∈ AC; K ∈ AB). Chứng minh rằng BH = CK.
Hướng dẫn giải
Xét tam giác BHA (vuông tại H) và tam giác CKA (vuông tại K) có:
AB = AC ( cân tại A)
là góc chung
⇒ (cạnh huyền – góc nhọn)
⇒ BH = CK (hai cạnh tương ứng)
Vậy BH = CK (đpcm).
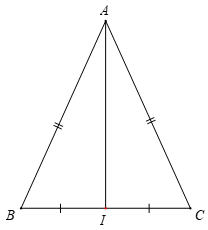
Bài 2. Cho tam giác ABC cân tại A. I là trung điểm của đoạn thẳng BC. Chứng minh AI vuông góc với BC và AI là tia phân giác của góc BAC.
Hướng dẫn giải
Xét tam giác AIB và tam giác AIC có:
AB = AC ( cân tại A)
BI = CI (theo giả thiết)
AI là cạnh chung
⇒ (c.c.c)
⇒ (hai góc tương ứng)
Mà
⇒
⇒ AI ⊥ BC (đpcm)
Vì (chứng minh trên)
⇒ (hai góc tương ứng)
⇒ AI là tia phân giác của góc BAC (đpcm).
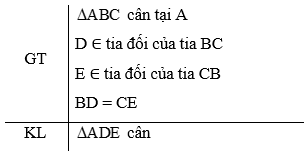
Bài 3. Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Chứng minh tam giác ADE là tam giác cân.
Hướng dẫn giải
cân tại A ⇒ (tính chất)
Mà: (hai góc kề bù)
(hai góc kề bù)
Do đó,
Xét tam giác ADB và tam giác AEC có:
AB = AC ( cân tại A)
(chứng minh trên)
BD = CE (theo giả thiết)
⇒ (c.g.c)
⇒ AD = AE (hai cạnh tương ứng)
⇒ cân tại A (đpcm).
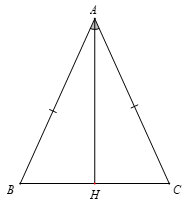
Bài 4. Cho tam giác ABC cân tại A có AH là đường phân giác của góc BAC (H ∈ BC). Chứng minh AH là đường trung trực của đoạn thẳng BC.
Hướng dẫn giải
Xét tam giác ABH và tam giác ACH có:
AB = AC ( cân tại A)
(AH là đường phân giác của )
AH là cạnh chung
⇒ (c.g.c)
⇒ HB = HC (hai cạnh tương ứng) (1)
Và (hai góc tương ứng)
Mà (hai góc kề bù)
⇒ ⇒ AH ⊥ BC (2)
Từ (1) và (2) ⇒AH là đường trung trực của đoạn thẳng BC (đpcm).
B. Trắc nghiệm Tam giác cân. Đường trung trực của đoạn thẳng (Kết nối tri thức 2023) có đáp án
I. Nhận biết
Câu 1. Phát biểu nào sau đây đúng nhất?
A. Tam giác cân là tam giác có hai cạnh bằng nhau;
B. Một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân;
C. Tam giác đều là tam giác có ba cạnh bằng nhau;
D. Cả A, B, C đều đúng.
Hướng dẫn giải
Đáp án: D
Giải thích:
⦁ Tam giác cân là tam giác có hai cạnh bằng nhau.
Suy ra phương án A đúng.
⦁ Trong một tam giác cân, hai góc ở đáy bằng nhau. Ngược lại, một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.
Suy ra phương án B đúng.
⦁ Tam giác đều là tam giác có ba cạnh bằng nhau.
Suy ra phương án C đúng.
Vậy ta chọn phương án D.
Câu 2. Đường trung trực của một đoạn thẳng là:
A. Đường thẳng đi qua trung điểm của đoạn thẳng đó;
B. Đường thẳng vuông góc với đoạn thẳng đó;
C. Đường thẳng vừa đi qua trung điểm, vừa vuông góc với đoạn thẳng đó;
D. Đường thẳng song song với đoạn thẳng đó.
Hướng dẫn giải
Đáp án: C
Giải thích:
Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng đó tại trung điểm của nó.
Vậy ta chọn phương án C.
Câu 3. Cho ∆ABC có AB = BC = 5 cm và C XXXv
. Khi đó ∆ABC là:
A. Tam giác đều;
B. Tam giác cân tại A;
C. Tam giác cân tại B;
D. Tam giác vuông cân.
Hướng dẫn giải
Đáp án: A
Giải thích:
Một tam giác có hai cạnh bằng nhau là tam giác cân.
Tam giác cân có một góc bằng 60° là tam giác đều.
Vì vậy ∆ABC là tam giác đều.
Vậy ta chọn phương án A.
Câu 4. Cho P là điểm nằm trên đường trung trực của đoạn thẳng CD. Kết luận nào sau đây đúng?
A. P là trung điểm của CD;
B. PC = PD;
C. DP = DC;
D. CP = CD.
Hướng dẫn giải
Đáp án: B
Giải thích:
Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
Vì vậy ta có P cách đều hai đầu mút của đoạn thẳng CD. Tức là, PC = PD.
Điểm P chưa chắc thuộc vào đoạn thẳng CD nên chưa thể kết luận P là trung điểm của đoạn thẳng CD được.
Vậy ta chọn phương án B.
Câu 5. Cho ∆MNP cân tại M và . Số đo của bằng:
A. 40°;
B. 100°;
C. 50°;
D. 90°.
Hướng dẫn giải
Đáp án: C
Giải thích:
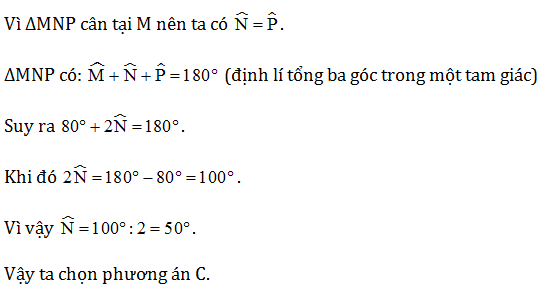
II. Thông hiểu
Câu 1. Cho đoạn thẳng CD. Gọi A là trung điểm của CD. Kẻ một đường thẳng vuông góc với CD tại A. Trên đường thẳng đó, lấy điểm B sao cho . Khi đó ∆BCD là tam giác gì?
A. Tam giác tù;
B. Tam giác đều;
C. Tam giác vuông cân;
D. Tam giác vuông.
Hướng dẫn giải
Đáp án: B
Giải thích:
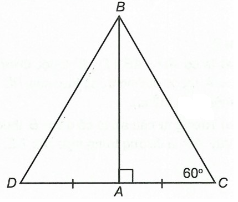
Ta có AC = AD (A là trung điểm của CD) và AB ⊥ CD (giả thiết)
Suy ra AB là đường trung trực của đoạn thẳng CD.
Do đó BD = BC (tính chất đường trung trực của một đoạn thẳng)
Vì vậy ∆BCD cân tại B.
Mà ∆BCD có (giả thiết)
Do đó ∆BCD là tam giác đều.
Vậy ta chọn phương án B.
Câu 2. Cho ∆ABC cân tại A. Lấy điểm D ∈ AC, E ∈ AB sao cho AD = AE. Gọi I là giao điểm của BD và CE. Kết luận nào sau đây đúng nhất?
A. AI là đường trung trực của đoạn thẳng BC;
B. ∆IBC cân tại I;
C. Cả A và B đều đúng;
D. Cả A và B đều sai.
Hướng dẫn giải
Đáp án: C
Giải thích:
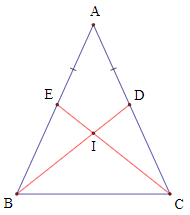
Xét ∆ABD và ∆ACE, có:
AB = AC (∆ABC cân tại A)
AD = AE (giả thiết)
là góc chung.
Do đó ∆ABD = ∆ACE (c.g.c)
Suy ra (cặp góc tương ứng)
Ta có (∆ABC cân tại A) và (chứng minh trên)
Suy ra .
Khi đó .
Suy ra ∆IBC cân tại I. Do đó phương án B đúng.
Vì ∆IBC cân tại I nên IB = IC, khi đó I thuộc đường trung trực của BC.
Mặt khác ∆ABC cân tại A nên AB = AC, khi đó A thuộc đường trung trực của BC.
Từ đó ta có AI là đường trung trực của BC.
Vậy ta chọn phương án C.
Câu 3. Cho ∆ABC vuông tại A có hai đường trung trực của hai cạnh AB và AC cắt nhau tại D. Vị trí của điểm D là:
A. D là trung điểm BC;
B. D là trung điểm của AB;
C. D là trung điểm của AC;
D. D là điểm trong tam giác ABC.
Hướng dẫn giải
Đáp án: A
Giải thích:
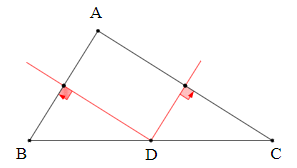
Gọi điểm M là giao điểm của đường trung trực của AB với BC.
Vì M thuộc trung trực của đoạn thẳng AB nên MA = MB.
Suy ra tam giác MAB cân tại M
⇒
Ta có: và
⇒
⇒ Tam giác MAC cân tại M
⇒ MA = MC ⇒ M thuộc đường trung trực của đoạn thẳng AC
Vậy M là giao điểm của hai đường trung trực của AB và AC hay ta có M trùng D.
Ta có DA = DB, DA = DC nên DB = DC
Vậy D là trung điểm của đoạn thẳng BC.
Câu 4. Cho ∆ABC có . Kẻ đường phân giác BD, từ D kẻ DE //BC (E ∈ AB). Số tam giác cân là:
A. 0;
B. 1;
C. 2;
D. 3.
Hướng dẫn giải
Đáp án: A
Giải thích:
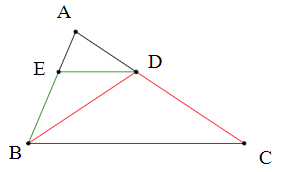
∆ABC có BD là đường phân giác.
Suy ra .
Do đó ∆BCD cân tại D.
Ta có BD // BC (giả thiết)
Suy ra (cặp góc so le trong)
Mà (chứng minh trên)
Do đó .
Suy ra ∆BED cân tại E.
Do đó có 2 tam giác cân
Vậy ta chọn phương án C.
Câu 5. Cho khác góc bẹt, từ một điểm M trên tia phân giác của . Từ M kẻ MA vuông góc với Ox và MB vuông góc với Oy. Phát biểu nào dưới đây là sai?
A. M cách đều hai cạnh của góc ;
B. ∆OAB đều;
C. OM là đường trung trực của đoạn thẳng AB;
D. ∆MAB cân tại M.
Hướng dẫn giải
Đáp án: B
Giải thích:
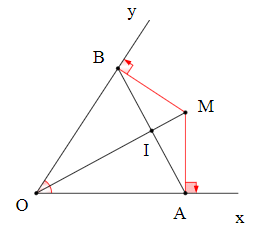
Xét ∆OAM và ∆OBM, có;
OM là cạnh chung.
(OM là tia phân giác của )
.
Do đó ∆OAM = ∆OBM (cạnh huyền – góc nhọn)
Suy ra OA = OB và MA = MB (các cặp cạnh tương ứng).
Do đó tam giác OAB cân tại O, tam giác MAB cân tại M và khoảng cách từ M đến hai cạnh của là bằng nhau. Vì vậy A và D đúng và B sai.
Khi đó OM là đường trung trực của đoạn thẳng AB. Do đó C đúng.
Vậy chọn đáp án B.
Câu 6. Cho ∆ABC đều. Lấy các điểm D, E, F lần lượt trên các cạnh AB, BC, CA sao cho AD = BE = CF. Khi đó ∆DEF là:
A. Tam giác cân;
B. Tam giác đều;
C. Tam giác vuông;
D. Tam giác vuông cân.
Hướng dẫn giải
Đáp án: B
Giải thích:
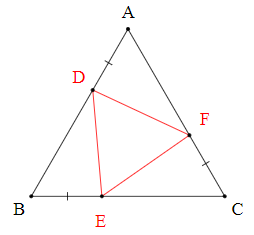
Vì ∆ABC đều nên ta có AB = BC = CA và .
Ta có AB = BC (chứng minh trên) và AD = BE (giả thiết).
Suy ra AB – AD = BC – BE.
Do đó BD = EC.
Xét ∆BDE và ∆CEF, có:
BD = EC (chứng minh trên)
BE = CF (giả thiết)
.
Do đó ∆BDE = ∆CEF (c.g.c)
Suy ra DE = EF (cặp cạnh tương ứng)
Chứng minh tương tự, ta thu được DE = DF và EF = DF.
Khi đó DE = DF = EF.
Vì vậy ∆DEF là tam giác đều.
Vậy ta chọn phương án B.
Câu 7. Cho ∆ABC vuông tại A, AB < AC. Tia phân giác của ![]() cắt AC tại E. Từ E kẻ ED vuông góc với BC tại D. Kết luận nào sau đây đúng nhất?
cắt AC tại E. Từ E kẻ ED vuông góc với BC tại D. Kết luận nào sau đây đúng nhất?
A. ∆ABE = ∆DBE;
B. ∆BAD cân tại B;
C. BE là đường trung trực của đoạn thẳng AD;
D. Cả A, B, C đều đúng.
Hướng dẫn giải
Đáp án: D
Giải thích:
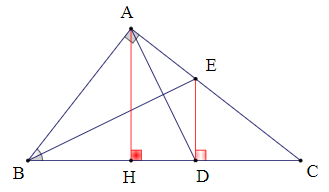
Xét ∆ABE và ∆DBE, có:
BE là cạnh chung.
(BE là phân giác của ![]() ).
).
.
Do đó ∆ABE = ∆DBE (cạnh huyền – góc nhọn)
Vì vậy phương án A đúng.
Ta có ∆ABE = ∆DBE (chứng minh trên)
Suy ra BA = BD và AE = DE (các cặp cạnh tương ứng)
Vì vậy BE là đường trung trực của đoạn thẳng AD.
Do đó phương án C đúng.
Vì BA = BD nên ∆BAD cân tại B.
Vì vậy phương án B đúng.
Vậy ta chọn phương án D.
Xem thêm tóm tắt lý thuyết Toán lớp 7 sách Kết nối tri thức hay, chi tiết khác:
Lý thuyết Bài 15: Các trường hợp bằng nhau của tam giác vuông
Lý thuyết Bài 17: Thu thập và phân loại dữ liệu
Xem thêm các chương trình khác:
- Giải sgk Lịch sử 7 – Kết nối tri thức
- Lý thuyết Lịch Sử 7 – Kết nối tri thức
- Giải sbt Lịch sử 7 – Kết nối tri thức
- Giải VTH Lịch sử 7 – Kết nối tri thức
- Soạn văn lớp 7 (hay nhất) – Kết nối tri thức
- Tác giả tác phẩm Ngữ văn lớp 7 – Kết nối tri thức
- Soạn văn lớp 7 (ngắn nhất) – Kết nối tri thức
- Tóm tắt tác phẩm Ngữ văn lớp 7 – Kết nối tri thức
- Bố cục tác phẩm Ngữ văn lớp 7 – Kết nối tri thức
- Nội dung chính tác phẩm Ngữ văn lớp 7 – Kết nối tri thức
- Văn mẫu lớp 7 – Kết nối tri thức
- Giải VTH Ngữ văn lớp 7 – Kết nối tri thức
- Giải sgk Địa Lí 7 – Kết nối tri thức
- Lý thuyết Địa Lí 7 – Kết nối tri thức
- Giải sbt Địa lí 7 – Kết nối tri thức
- Giải VTH Địa lí 7 – Kết nối tri thức
- Giải sgk Tiếng Anh 7 Global Success – Kết nối tri thức
- Giải sbt Tiếng Anh 7 Global Success - Kết nối tri thức
- Bài tập Tiếng Anh 7 Global success theo Unit có đáp án
- Trọn bộ Từ vựng Tiếng Anh 7 Global success đầy đủ nhất
- Ngữ pháp Tiếng Anh 7 Global success
- Giải sgk Giáo dục công dân 7 – Kết nối tri thức
- Lý thuyết GDCD 7 – Kết nối tri thức
- Giải sbt Giáo dục công dân 7 – Kết nối tri thức
- Giải vth Giáo dục công dân 7 – Kết nối tri thức
- Giải sgk Khoa học tự nhiên 7 – Kết nối tri thức
- Lý thuyết Khoa học tự nhiên 7 – Kết nối tri thức
- Giải sbt Khoa học tự nhiên 7 – Kết nối tri thức
- Giải sbt Hoạt động trải nghiệm lớp 7 - KNTT
- Giải sgk Hoạt động trải nghiệm 7 - KNTT
- Giải sgk Công nghệ 7 – Kết nối tri thức
- Lý thuyết Công nghệ 7 – Kết nối tri thức
- Giải sbt Công nghệ 7 – Kết nối tri thức
- Giải VTH Công nghệ 7 – KNTT
- Giải sgk Tin học 7 – Kết nối tri thức
- Lý thuyết Tin học 7 – Kết nối tri thức
- Giải sbt Tin học 7 – Kết nối tri thức
- Giải VTH Tin học 7 – Kết nối tri thức
- Giải sgk Giáo dục thể chất 7 – Kết nối tri thức
- Giải sgk Âm nhạc 7 – Kết nối tri thức