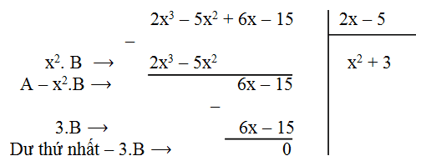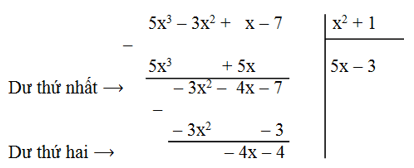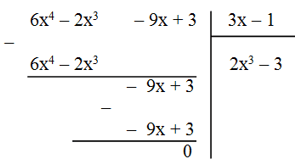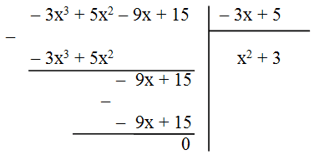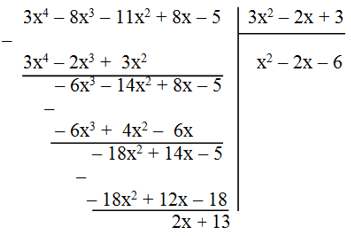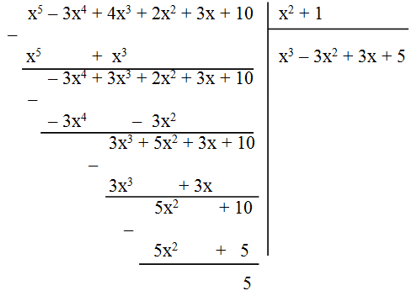Lý thuyết Phép chia đa thức một biến – Toán lớp 7 Kết nối tri thức
Với lý thuyết Toán lớp 7 Bài 28: Phép chia đa thức một biến chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sách Kết nối tri thức sẽ giúp học sinh nắm vững kiến thức trọng tâm để học tốt môn Toán 7.
A. Lý thuyết Toán 7 Bài 28: Phép chia đa thức một biến - Kết nối tri thức
1. Làm quen phép chia đa thức
• Cho hai đa thức A và B (B ≠ 0). Nếu có một đa thức Q sao cho A = B.Q thì ta có phép chia hết:
A : B = Q (hay ), trong đó
A là đa thức bị chia;
B là đa thức chia (kí hiệu B ≠ 0 có nghĩa B không phải là đa thức không).
Q là đa thức thương (gọi tắt là thương).
Khi đó ta còn nói đa thức A chia hết cho đa thức B.
• Cho hai đơn thức axm và bxn (m; n ∈ ℕ, a; b ∈ ℝ, b ≠ 0).
Khi đó nếu m ≥ n thì ta có phép chia axm cho bxn là phép chia hết và ta có:
axm : bxn = xm – n (quy ước: x0 = 1).
Ví dụ:
+ Tính 3x7 : ta làm như sau: 3x7 : = = – 6x3.
Chú ý:
• axm : bxn được hiểu là axm : (bxn)
Chẳng hạn: 4x5 : 2x2 được hiểu là 4x5 : (2x2).
2. Chia đa thức cho đa thức
• Muốn chia một đa thức cho một đa thức, ta đặt tính và chia (tương tự phép chia hai số tự nhiên) cho đến khi được đa thức dư là đa thức không, hoặc có bậc nhỏ hơn bậc của đa thức chia.
• Khi đặt tính chia, nếu đa thức ở một dòng khuyết một hạng tử bậc nào đó thì ta để một khoảng trống ứng với hạng tử đó.
• Nếu chia đa thức A cho đa thức B, ta được đa thức thương là Q, đa thức dư là R thì:
+ Đa thức dư R = 0 (khi chia hết) hoặc R là đa thức có bậc nhỏ hơn đa thức B (nếu không chia hết).
+ Ta có đẳng thức: A = B.Q + R.
Ví dụ:
+ Cho A = 2x3 – 5x2 + 6x – 15; B = 2x – 5. Để tính A : B ta làm như sau:
Dư cuối cùng bằng 0 nên quá trình chia kết thúc.
Vậy phép chia đa thức A cho đa thức B là phép chia hết, có đa thức thương là x2 + 3.
+ Cho đa thức P = 5x3 – 3x2 + x – 7; Q(x) = x2 + 1. Để tính P : Q ta làm như sau
Dư cuối cùng có bậc thấp hơn bậc của đa thức chia nên quá trình chia kết thúc.
Vậy phép chia đa thức P cho đa thức Q là phép chia có dư, có đa thức thương là 5x – 3, đa thức dư là – 4x – 4.
Chú ý: Khi chia đa thức cho một đơn thức có thể không cần đặt tính chia.
Chẳng hạn chia đa thức 6x3 – 2x2 + x cho đơn thức 0,5x, ta làm như sau:
(6x3 – 2x2 + x) : 0,5x
= 6x3 : 0,5x – 2x2 : 0,5x + x : 0,5x
= 12x2 – 4x + 2.
Bài tập Phép chia đa thức một biến
Bài 1. Tính
a) 9x6 : 3x3;
b) 225x7 : (– 25x2);
c) (– x)3 : x;
d) (– 4,62x5) : (–3x4).
Hướng dẫn giải
a) 9x6 : 3x3 = (9 : 3)(x6 : x3) = 3x6 – 3 = 3x3.
b) 225x7 : (– 25x2) = [225 : (– 25)](x7 : x2) = – 9x7 – 2 = – 9x5.
c) (– x)3 : x = (– x3) : x = (x3 : x) = – 4x3 – 1 = – 4x2.
d) (– 4,62x5) : (–3x4) = [(– 4,62) : (–3)](x5 : x4) = 1,54x5 – 4 = 1,54x.
Bài 2. Thực hiện các phép chia sau:
a) (– 10x3 + 25x2 – 8x) : (– 5x);
b) (2x5 + 6x3 – 3x2) : 2x2.
Hướng dẫn giải
a) (– 10x3 + 25x2 – 8x) : (– 5x)
= (– 10x3) : (– 5x) + (25x2) : (– 5x) – (8x) : (– 5x)
= 2x2 – 5x + .
b) (2x5 + 6x3 – 3x2) : 2x2
= 2x5 : 2x2 + 6x3 : 2x2 – 3x2 : 2x2
= x3 + 3x – .
Bài 3. Thực hiện các phép chia đa thức sau bằng cách đặt tính chia:
a) (6x4 – 2x3 – 9x + 3) : (3x – 1);
b) (– 3x3 + 5x2 – 9x + 15) : (– 3x + 5);
c) (3x4 – 8x3 – 11x2 + 8x – 5) : (3x2 – 2x + 3);
d) (x5 – 3x4 + 4x3 + 2x2 + 3x + 10) : (x2 + 1).
Hướng dẫn giải
a) (6x4 – 2x3 – 9x + 3) : (3x – 1)
Vậy (6x4 – 2x3 – 9x + 3) : (3x – 1) = 2x3 – 3.
b) (– 3x3 + 5x2 – 9x + 15) : (– 3x + 5)
Vậy (– 3x3 + 5x2 – 9x + 15) : (– 3x + 5) = x2 + 3.
c) (3x4 – 8x3 – 11x2 + 8x – 5) : (3x2 – 2x + 3)
Vậy (3x4 – 8x3 – 11x2 + 8x – 5) : (3x2 – 2x + 3) = x2 – 2x – 6 dư 2x + 13.
d) (x5 – 3x4 + 4x3 + 2x2 + 3x + 10) : (x2 + 1)
Vậy (x5 – 3x4 + 4x3 + 2x2 + 3x + 10) : (x2 + 1) = x3 – 3x2 + 3x + 5 dư 5.
Xem thêm tóm tắt lý thuyết Toán lớp 7 sách Kết nối tri thức hay, chi tiết khác:
Lý thuyết Ôn tập Chương 7 – Toán 7 Kết nối tri thức
Lý thuyết Bài 29: Làm quen với biến cố
Lý thuyết Bài 30: Làm quen với xác suất của biến cố
Lý thuyết Bài 31: Quan hệ giữa góc và cạnh đối diện trong một tam giác
Xem thêm các chương trình khác:
- Giải sgk Lịch sử 7 – Kết nối tri thức
- Lý thuyết Lịch Sử 7 – Kết nối tri thức
- Giải sbt Lịch sử 7 – Kết nối tri thức
- Giải VTH Lịch sử 7 – Kết nối tri thức
- Soạn văn lớp 7 (hay nhất) – Kết nối tri thức
- Tác giả tác phẩm Ngữ văn lớp 7 – Kết nối tri thức
- Soạn văn lớp 7 (ngắn nhất) – Kết nối tri thức
- Tóm tắt tác phẩm Ngữ văn lớp 7 – Kết nối tri thức
- Bố cục tác phẩm Ngữ văn lớp 7 – Kết nối tri thức
- Nội dung chính tác phẩm Ngữ văn lớp 7 – Kết nối tri thức
- Văn mẫu lớp 7 – Kết nối tri thức
- Giải VTH Ngữ văn lớp 7 – Kết nối tri thức
- Giải sgk Địa Lí 7 – Kết nối tri thức
- Lý thuyết Địa Lí 7 – Kết nối tri thức
- Giải sbt Địa lí 7 – Kết nối tri thức
- Giải VTH Địa lí 7 – Kết nối tri thức
- Giải sgk Tiếng Anh 7 Global Success – Kết nối tri thức
- Giải sbt Tiếng Anh 7 Global Success - Kết nối tri thức
- Bài tập Tiếng Anh 7 Global success theo Unit có đáp án
- Trọn bộ Từ vựng Tiếng Anh 7 Global success đầy đủ nhất
- Ngữ pháp Tiếng Anh 7 Global success
- Giải sgk Giáo dục công dân 7 – Kết nối tri thức
- Lý thuyết GDCD 7 – Kết nối tri thức
- Giải sbt Giáo dục công dân 7 – Kết nối tri thức
- Giải vth Giáo dục công dân 7 – Kết nối tri thức
- Giải sgk Khoa học tự nhiên 7 – Kết nối tri thức
- Lý thuyết Khoa học tự nhiên 7 – Kết nối tri thức
- Giải sbt Khoa học tự nhiên 7 – Kết nối tri thức
- Giải sbt Hoạt động trải nghiệm lớp 7 - KNTT
- Giải sgk Hoạt động trải nghiệm 7 - KNTT
- Giải sgk Công nghệ 7 – Kết nối tri thức
- Lý thuyết Công nghệ 7 – Kết nối tri thức
- Giải sbt Công nghệ 7 – Kết nối tri thức
- Giải VTH Công nghệ 7 – KNTT
- Giải sgk Tin học 7 – Kết nối tri thức
- Lý thuyết Tin học 7 – Kết nối tri thức
- Giải sbt Tin học 7 – Kết nối tri thức
- Giải VTH Tin học 7 – Kết nối tri thức
- Giải sgk Giáo dục thể chất 7 – Kết nối tri thức
- Giải sgk Âm nhạc 7 – Kết nối tri thức