Lý thuyết Ôn tập Chương 10 – Toán 7 Kết nối tri thức

. Lý thuyết Toán 7 Ôn tập Chương 10 - Kết nối tri thức

1. Hình hộp chữ nhật, hình lập phương

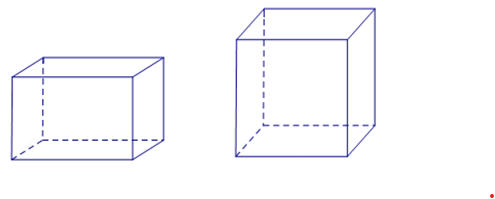
+ Hình hộp chữ nhật có 6 mặt là các hình chữ nhật, 8 đỉnh, 12 cạnh, 4 đường chéo, các cạnh bên song song và bằng nhau.

+ Hình lập phương là hình hộp chữ nhật có 6 mặt là các hình vuông.

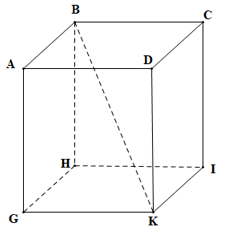
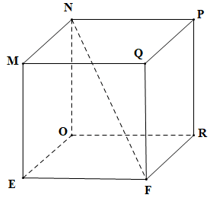
Ví dụ: Kể tên các đỉnh, cạnh, đường chéo, mặt bên, mặt đáy của hình hộp chữ nhật ABCD.GHIK và hình lập phương MNPQ.EORF (hình vẽ).

Hướng dẫn giải

a) Hình hộp chữ nhật:

- Hình hộp chữ nhật ABCD.GHIK có:

+) 8 đỉnh là A, B, C, D, G, H, I, K;

+) 12 cạnh là AB, BC, CD, DA, GH, HI, IK, KG, AG, BH, CI, DK;

+) 4 đường chéo là AI, BK, CG, DH;

+) 4 mặt bên là ABHG, BHIC, CIKD, ADKG và 2 mặt đáy là ABCD, GHIK. Các mặt bên và mặt đáy là các hình chữ nhật.

b) Hình lập phương:

- Hình lập phương MNPQ.EORF có :

+) 8 đỉnh là M, N, P, Q, E, O, R, F;

+) 12 cạnh là MN, NP, PQ, QM, EO, OR, RF, FE, ME, NO, PR, QF;

+) 4 đường chéo là MR, NF, PE, QO;

+) 4 mặt bên là MNOE, NORP, PRFQ, MEFQ và 2 mặt đáy là MNPQ, EORF. Các mặt bên và mặt đáy là các hình vuông.

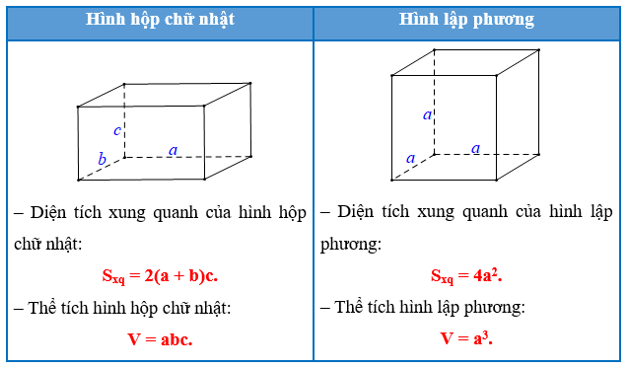
2. Diện tích xung quanh và thể tích của hình hộp chữ nhật, hình lập phương

Chú ý: Khi tính diện tích, thể tích của một hình, các kích thước của nó phải cùng đơn vị độ dài.

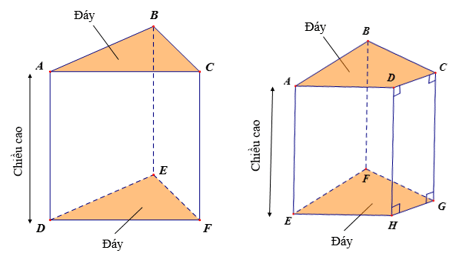
3. Hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác

–Trong hình lăng trụ đứng tam giác (tứ giác):

+ Hai mặt đáy song song với nhau.

+ Các mặt bên là những hình chữ nhật.

+ Các cạnh bên song song và bằng nhau.

–Độ dài một cạnh bên gọi là chiều cao của lăng trụ đứng.

–Hình hộp chữ nhật và hình lập phương cũng là các hình lăng trụ đứng tứ giác

Chú ý:Sàn nhà và trần nhà là hình ảnh của hai mặt song song.

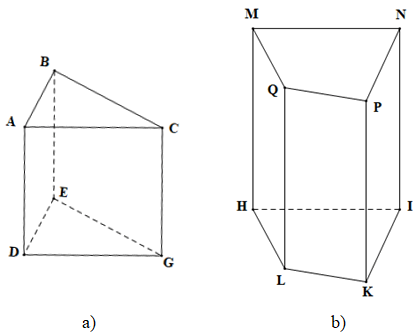
Ví dụ: Kể tên các đỉnh, cạnh đáy, cạnh bên, mặt bên, mặt đáy của các hình lăng trụ đứng sau:

Hướng dẫn giải

Hình a) là hình lăng trụ đứng tam giác ABC.DEG có:

+ Các đỉnh là A, B, C, D, E, G;

+ Các cạnh đáy là AB, BC, AC, DE, EG, DG;

+ Các cạnh bên là AD, BE, CG;

+ Các mặt bên là các hình chữ nhật ABED, BCGE, ACGD;

+ Hai mặt đáy là các tam giác ABC, DEG.

Hình b) là hình lăng trụ đứng tứ giác MNPQ.HIKL có:

+ Các đỉnh là M, N, P, Q, H, I, K, L;

+ Các cạnh đáy là MN, NP, PQ, QM, HI, IK, KL, LH;

+ Các cạnh bên là MH, NI, PK, QL;

+ Các mặt bên là các hình chữ nhật MNIH, MQLH, QPKL, PNIK;

+ Hai mặt đáy là các tứ giác MNPQ, HIKL.

4. Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác

Bài tập Tổng hợp Toán 7 Chương 10

Bài 1. Trong các đồ vật sau, đồ vật nào có dạng hình hộp chữ nhật, đồ vật nào có hình lập phương?

Lời giải

Đồ vật có dạng hình hộp chữ nhật là: quyển sách, hộp bánh quy, hộp giấy lụa.

Đồ vật có dạng hình lập phương là: Con xúc xắc, hộp quà.

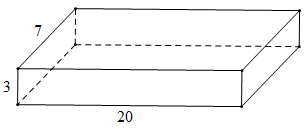
Bài 2. Một bể bơi có chiều dài 20 m, chiều rộng 7 m, sâu 3 m. Hỏi người thợ phải dùng bao nhiêu viên gạch ốp lát để lát đáy và xung quanh thành bể đó? Biết rằng mỗi viên gạch có chiều dài 40 cm, rộng 25 cm và coi diện tích mạch vữa lát không đáng kể.

Hướng dẫn giải

Diện tích đáy bể là:

20 . 7 = 140 (m²).

Diện tích xung quanh thành bể là:

2 . (20 + 7) . 3 = 162 (m²).

Diện tích cần lát gạch là:

140 + 162 = 302 (m²).

Diện tích một viên gạch là:

40. 25 = 1 000 (cm²) = 0,1 (m²).

Số viên gạch ốp lát cần dùng là:

302 : 0,1 = 3 020 (viên)

Vậy số viên gạch ốp tường cần dùng 3 020 viên.

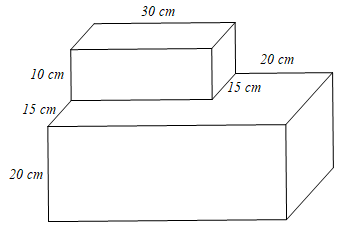
Bài 3. Cho một khối bê tông kích thước như hình vẽ sau:

a) Tính thể tích của khối bê tông đó.

b) Người ta muốn sơn khối bê tông đó trừ mặt tiếp giáp với đất, tính chi phí sơn biết mỗi mét vuông tốn 50 000 đồng.

Hướng dẫn giải

a) Chiều dài của hình hộp chữ nhật phía dưới là:

30 + 20 = 50 (cm).

Chiều rộng của hình hộp chữ nhật phía dưới là :

15 + 15 = 30 (cm).

Thể tích hình hộp chữ nhật phía dưới là:

50 . 30 . 20 = 30 000 (cm³).

Thể tích hình hộp chữ nhật phía trên là:

30 . 15 . 10 = 4 500 (cm³).

Thể tích của khối bê tông là:

30 000 + 4 500 = 34 500 (cm³).

Vậy thể tích khối bê tông là 34 500 cm³.

b) Diện tích xung quanh của hình hộp chữ nhật phía dưới là:

2 . (50 + 30) . 20 = 3 200 (cm²).

Diện tích xung quanh của hình hộp chữ nhật phía trên là:

2 . (30 + 15) . 10 = 900 (cm²).

Diện tích phần tiếp giáp giữa hai hình hộp chữ nhật chính là diện tích mặt đáy của hình hộp chữ nhật phía trên.

Do đó diện tích của các mặt nằm ngang cần sơn của khối bê tông bằng diện tích mặt đáy hình hộp chữ nhật phía dưới.

Diện tích đó là: 50 . 30 = 1 500 (cm²).

Diện tích của phần bê tông muốn sơn là:

3 200 + 900 + 1 500 = 5 600 (cm²) = 0,56 (m²).

Chi phí để sơn khối bê tông đó là:

0,56 . 50 000 = 28 000 (đồng)

Vậy muốn sơn khối bê tông cần chi phí là 28 000 đồng.

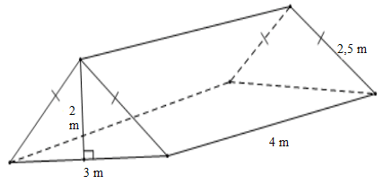
Bài 4. Một cái lều chữ A dạng hình lăng trụ đứng tam giác có kích thước như hình vẽ:

a) Tính thể tích khoảng không bên trong lều.

b) Biết lều phủ bạt bốn phía (trừ mặt tiếp đất), tính diện tích vải bạt cần có để dựng lều.

Hướng dẫn giải

a) Diện tích một mặt đáy của hình lăng trụ đứng tam giác là:

$\frac{1}{2}$. 2 . 3 = 3 (m²)

Thể tích khoảng không bên trong lều là:

3 . 4 = 12 (m³).

Vậy thể tích khoảng không bên trong lều là 12 m³.

b) Diện tích xung quanh lăng trụ đứng tam giác là:

(2,5 + 2,5 + 3) . 4 = 32 (m²).

Diện tích tất cả các mặt của hình lăng trụ đứng tam giác là:

32+ 2 . 3 = 38(m²).

Diện tích mặt tiếp đất là: 3 . 4 = 12(m²).

Diện tích vải bạt cần có để dựng lều chính là diện tích tất cả các mặt của lăng trụ đứng tam giác trừ đi diện tích mặt tiếp đất. Do đó diện tích vải bạt cần là:

38 – 12 = 26 (m²).

Vậy diện tích vải bạt cần để dựng lều là 26 m².

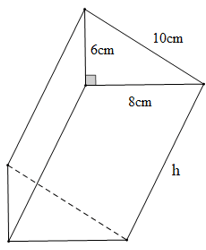
Bài 5. Cho hình lăng trụ đứng tam giác vuông có độ dài ba cạnh đáy là 6 cm, 8 cm, 10 cm. Biết diện tích xung quanh của hình lăng trụ đólà 288 cm². Tính thể tích lăng trụ đó.

Hướng dẫn giải

Diện tích một mặt đáy của hình lăng trụ đứng tam giác đó là:

$\frac{1}{2}$. 6 . 8 = 24 (cm²).

Diện tích xung quanh của hình lăng trụ đứng tam giác đó được tính bởi:

(6 + 10 + 8) . h = 24h (cm²)

Mà diện tích xung quanh của hình lăng trụ đứng tam giác đó là 288 cm² nên ta có:

24h = 288

Suy ra: h = 12 (cm).

Thể tích lăng trụ đó là:

24 . 12 = 288 (cm³)

Vậy thể tích lăng trụ đứng tam giác là 288 cm³.

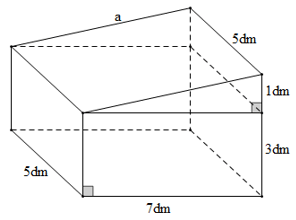
Bài 6. Một khối bê tôngcó kích thước như hình vẽ:

Hãy tính chi phí để đúc khối bê tông trên. Biết chi phí để đúc 1 m³ bê tông là 1,2 triệu đồng.

Hướng dẫn giải

Diện tích mặt đáy của khối bê tông có dạng hình lăng trụ đứng tứ giác là:

$\frac{1}{2}$. (3 + 4) . 7 = 24,5 (dm²).

Thể tích khối bê tông đó là:

24,5 . 5 = 122,5 (dm³) = 0,1225 m³.

Chi phí để đúc khối bê tông đó là:

0,1225 . 1,2 = 0,135 (triệu đồng) = 135 000 đồng

Vậy chi phí để đúc khối bê tông đó là 135 000 đồng.

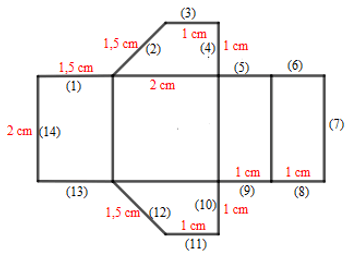
Bài 7. Cho tấm bìa có các kích thước như sau:

Phải gấp các cạnh nào của tấm bìa với nhau để được một hình lăng trụ đứng tứ giác? Cho biết chiều cao của tứ giác đó.

Hướng dẫn giải

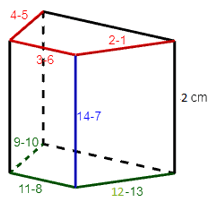
Ta phải gấp các cặp cạnh sau đây với nhau để hình trên trở thành một hình lăng trụ đứng tứ giác: (1) và (2), (4) và (5), (3) và (6), (12) và (13), (9) và (10), (8) và (11), (7) và (14).

Khi đó ta có hình lăng trụ đứng tứ giác như sau:

Vậy chiều cao của hình lăng trụ đứng trên là: 2 cm.

Xem thêm tóm tắt lý thuyết Toán lớp 7 sách Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài 12: Tổng các góc trong một tam giác

Lý thuyết Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác

Lý thuyết Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác

Lý thuyết Bài 15: Các trường hợp bằng nhau của tam giác vuông

Lý thuyết Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng