Giải Toán 9 trang 75 Tập 1 Kết nối tri thức
Với giải bài tập Toán lớp 9 trang 75 trong Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng sách Kết nối tri thức Tập 1 hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán lớp 9 trang 75 Tập 1.
Giải Toán 9 trang 75 Tập 1
Lời giải:
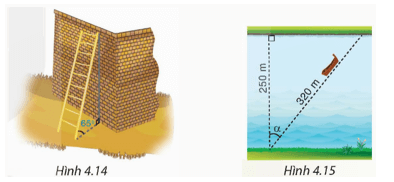
Giả sử trong hình dưới đây, BC là độ dài thang và AB là khoảng cách từ chân thang đến chân tường.
Xét ∆ABC vuông tại A, theo định lí 1, ta có:
AB = BC.cosB = 3.cos65° ≈ 1,27 (m).
Vậy cần đặt chân thang cách chân tường một khoảng 1,27 m để bó tạo được với mặt đất một góc “an toàn” 65°.
Lời giải:
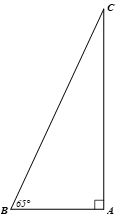
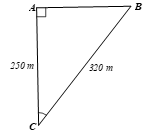
Giả sử trong hình vẽ dưới đây, AC là độ rộng của khúc sông và BC là quãng đường con đò đã di chuyển từ bờ bên này sang bờ bên kia.
Xét ∆ABC vuông tại A, theo định nghĩa tỉ số lượng giác côsin, ta có:
Từ đó tìm được α ≈ 38°37’.
Vậy dòng nước đã đẩy con đò đi lệch một góc α ≈ 38°37’.
2. Hệ thức giữa hai cạnh góc vuông
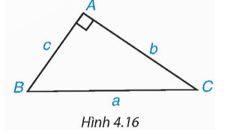
HĐ2 trang 75 Toán 9 Tập 1: Xét tam giác ABC trong Hình 4.16.
a) Viết các tỉ số lượng giác tang, côtang của góc B và góc C theo b, c.
b) Tính mỗi cạnh góc vuông b và c theo cạnh góc vuông kia và các tỉ số lượng giác trên của góc B và góc C.
Lời giải:
a) Xét ∆ABC vuông tại A, theo định nghĩa tỉ số lượng giác và định lí về tỉ số lượng giác của hai góc phụ nhau, ta có:
b) Từ ta có b = c.tanB = c.cotC.
Từ ta có c = btanC = bcotB.
Xem thêm lời giải bài tập Toán 9 sách Kết nối tri thức hay, chi tiết khác:
Xem thêm lời giải bài tập Toán 9 sách Kết nối tri thức hay, chi tiết khác:
Mở đầu trang 74 Toán 9 Tập 1: Để đo chiều cao của một toà lâu đài (H.4.11), người ta đặt giác kế...
HĐ1 trang 74 Toán 9 Tập 2: Cho tam giác ABC vuông tại A, cạnh huyền a và các cạnh góc vuông b, c....
Luyện tập 1 trang 75 Toán 9 Tập 1: Một chiếc thang dài 3 m. Cần đặt chân thang cách chân tường..
Luyện tập 1 trang 75 Toán 9 Tập 1: Một khúc sông rộng khoảng 250 m. Một con đò chèo qua sông...
HĐ2 trang 75 Toán 9 Tập 1: Xét tam giác ABC trong Hình 4.16....
Luyện tập 2 trang 76 Toán 9 Tập 1: Bóng trên mặt đất của một cây dài 25 m. Tính chiều cao của cây...
Luyện tập 3 trang 77 Toán 9 Tập 1: Cho tam giác vuông ABC có cạnh góc vuông AB = 4...
Câu hỏi trang 77 Toán 9 Tập 1: Hãy nêu cách giải tam giác ABC vuông tại A khi biết cạnh góc vuông AB...
Luyện tập 4 trang 77 Toán 9 Tập 1: Giải tam giác ABC vuông tại A, biết BC = 9, ...
Vận dụng trang 77 Toán 9 Tập 1: Giải bài toán ở tình huống mở đầu với α = 27° và β = 19°....
Bài 4.8 trang 78 Toán 9 Tập 1: Giải tam giác ABC vuông tại A có BC = a, AC = b, AB = c,...
Bài 4.9 trang 78 Toán 9 Tập 1: Tính góc nghiêng α của thùng xe chở rác trong Hình 4.22....
Bài 4.11 trang 78 Toán 9 Tập 1: Tính các góc của hình thoi có hai đường chéo...
Bài 4.12 trang 78 Toán 9 Tập 1: Cho hình thang ABCD (AD // BC) có AD = 16 cm, BC = 4 cm...
Xem thêm lời giải bài tập Toán 9 sách Kết nối tri thức hay, chi tiết khác:
Bài tập cuối chương 3 trang 65
Xem thêm các chương trình khác:
- Soạn văn 9 Kết nối tri thức (hay nhất)
- Văn mẫu 9 - Kết nối tri thức
- Tóm tắt tác phẩm Ngữ văn 9 – Kết nối tri thức
- Tác giả tác phẩm Ngữ văn 9 - Kết nối tri thức
- Bố cục tác phẩm Ngữ văn 9 – Kết nối tri thức
- Nội dung chính tác phẩm Ngữ văn 9 – Kết nối tri thức
- Soạn văn 9 Kết nối tri thức (ngắn nhất)
- Bài tập Tiếng Anh 9 Global success theo Unit có đáp án
- Giải sgk Tiếng Anh 9 - Global success
- Trọn bộ Từ vựng Tiếng Anh 9 Global success đầy đủ nhất
- Trọn bộ Ngữ pháp Tiếng Anh 9 Global success đầy đủ nhất
- Giải sbt Tiếng Anh 9 – Global Success
- Giải sgk Khoa học tự nhiên 9 – Kết nối tri thức
- Lý thuyết Khoa học tự nhiên 9 – Kết nối tri thức
- Giải sbt Khoa học tự nhiên 9 – Kết nối tri thức
- Giải sgk Lịch sử 9 – Kết nối tri thức
- Giải sbt Lịch sử 9 – Kết nối tri thức
- Giải sgk Địa lí 9 – Kết nối tri thức
- Giải sbt Địa lí 9 – Kết nối tri thức
- Giải sgk Tin học 9 – Kết nối tri thức
- Giải sbt Tin học 9 – Kết nối tri thức
- Giải sgk Công nghệ 9 – Kết nối tri thức
- Giải sgk Giáo dục công dân 9 – Kết nối tri thức
- Giải sbt Giáo dục công dân 9 – Kết nối tri thức
- Giải sgk Hoạt động trải nghiệm 9 – Kết nối tri thức