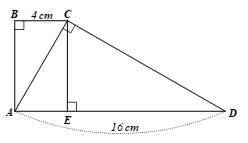
Cho hình thang ABCD (AD // BC) có AD = 16 cm, BC = 4 cm và góc A = góc B = góc ACD = 90 độ

Lời giải Bài 4.12 trang 78 Toán 9 Tập 1 Toán 9 Tập 1 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 Tập 1.

1 1,327 20/04/2024

Trang trước

Trang sau

Giải Toán 9 Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng

Bài 4.12 trang 78 Toán 9 Tập 1: Cho hình thang ABCD (AD // BC) có AD = 16 cm, BC = 4 cm và $\hat{A} = \hat{B} = \hat{A C D} = 90 ° .$

a) Kẻ đường cao CE của tam giác ACD. Chứng minh $\hat{A D C} = \hat{A C E} .$ Tính sin của các góc $\hat{A D C}, \hat{A C E}$ và suy ra AC² = AE.AD. Từ đó tính AC.

b) Tính góc D của hình thang.

Lời giải:

Bài 4.12 trang 78 Toán 9 Tập 1 | Kết nối tri thức Giải Toán 9

a) Ta có $\hat{A D C} + \hat{D C E} = 90 °$ (hai góc nhọn trong ∆CDE vuông tại E) và $\hat{A C E} + \hat{D C E} = \hat{A C D} = 90 °$ nên $\hat{A D C} = \hat{A C E}$ (cùng phụ góc $\hat{D C E}) .$ (1)

Xét ∆ACD vuông tại C, ta có $\sin \hat{A D C} = \frac{A C}{A D} .$ (2)

Xét ∆ACE vuông tại E, ta có $\sin \hat{A C E} = \frac{A E}{A C} .$ (3)

Từ (1), (2) và (3) ta suy ra $\frac{A C}{A D} = \frac{A E}{A C},$ do đó AC² = AE.AD.

Hình thang ABCD có AD // BC và AB ⊥ BC (do $\hat{B} = 90 °)$ nên AB ⊥ AD.

Tứ giác ABCE có $\hat{A} = \hat{B} = \hat{E} = 90 °$ nên ABCE là hình chữ nhật.

Suy ra AE = BC = 4 cm (tính chất hình chữ nhật).

Khi đó, AC² = 4.16 = 64 nên AC = 8 (cm) (do AC > 0).

b) Theo câu a, ta có $\sin \hat{A D C} = \frac{A C}{A D} = \frac{8}{16} = \frac{1}{2},$ suy ra $\hat{D} = 30 ° .$

Xem thêm lời giải bài tập Toán 9 sách Kết nối tri thức hay, chi tiết khác:

Mở đầu trang 74 Toán 9 Tập 1: Để đo chiều cao của một toà lâu đài (H.4.11), người ta đặt giác kế...

HĐ1 trang 74 Toán 9 Tập 2: Cho tam giác ABC vuông tại A, cạnh huyền a và các cạnh góc vuông b, c....

Luyện tập 1 trang 75 Toán 9 Tập 1: Một chiếc thang dài 3 m. Cần đặt chân thang cách chân tường..

Luyện tập 1 trang 75 Toán 9 Tập 1: Một khúc sông rộng khoảng 250 m. Một con đò chèo qua sông...

HĐ2 trang 75 Toán 9 Tập 1: Xét tam giác ABC trong Hình 4.16....

Luyện tập 2 trang 76 Toán 9 Tập 1: Bóng trên mặt đất của một cây dài 25 m. Tính chiều cao của cây...

Luyện tập 3 trang 77 Toán 9 Tập 1: Cho tam giác vuông ABC có cạnh góc vuông AB = 4...

Câu hỏi trang 77 Toán 9 Tập 1: Hãy nêu cách giải tam giác ABC vuông tại A khi biết hai cạnh AB = c,...

Câu hỏi trang 77 Toán 9 Tập 1: Hãy nêu cách giải tam giác ABC vuông tại A khi biết cạnh góc vuông AB...

Luyện tập 4 trang 77 Toán 9 Tập 1: Giải tam giác ABC vuông tại A, biết BC = 9, $\hat{C} = 53 ° .$ ...

Vận dụng trang 77 Toán 9 Tập 1: Giải bài toán ở tình huống mở đầu với α = 27° và β = 19°....

Bài 4.8 trang 78 Toán 9 Tập 1: Giải tam giác ABC vuông tại A có BC = a, AC = b, AB = c,...

Bài 4.9 trang 78 Toán 9 Tập 1: Tính góc nghiêng α của thùng xe chở rác trong Hình 4.22....

Bài 4.10 trang 78 Toán 9 Tập 1: Tìm góc nghiêng α và chiều rộng AB của mái nhà kho trong Hình 4.23....

Bài 4.11 trang 78 Toán 9 Tập 1: Tính các góc của hình thoi có hai đường chéo...

Bài 4.12 trang 78 Toán 9 Tập 1: Cho hình thang ABCD (AD // BC) có AD = 16 cm, BC = 4 cm...

Bài 4.13 trang 78 Toán 9 Tập 1: Một người đứng tại điểm A, cách gương phẳng đặt nằm trên mặt đất tại điểm B ...

Xem thêm lời giải bài tập Toán 9 sách Kết nối tri thức hay, chi tiết khác:

Luyện tập chung trang 63

Bài tập cuối chương 3 trang 65

Bài 11: Tỉ số lượng giác của góc nhọn

Luyện tập chung trang 80

Bài tập cuối chương 4 trang 81

1 1,327 20/04/2024

Trang trước

Trang sau

Xem thêm các chương trình khác: