Nội dung bài viết

    Xem thêm

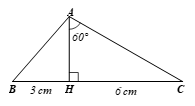
    Cho tam giác ABC có chân đường cao AH nằm giữa B và C. Biết HB = 3 cm, HC = 6 cm, góc HAC = 60 độ

    Lời giải Bài 4.15 trang 80 Toán 9 Tập 1 Toán 9 Tập 1 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 Tập 1.

    1 1,560 20/04/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 9 Luyện tập chung trang 80

    Bài 4.15 trang 80 Toán 9 Tập 1: Cho tam giác ABC có chân đường cao AH nằm giữa B và C. Biết HB = 3 cm, HC = 6 cm, HAC^=60°. Hãy tính độ dài các cạnh (làm tròn đến cm), số đo các góc của tam giác ABC (làm tròn đến độ).

    Lời giải:

    Bài 4.15 trang 80 Toán 9 Tập 1 | Kết nối tri thức Giải Toán 9

    – Ta có: BC = BH + HC = 3 + 6 = 9 cm.

    Xét ∆AHC vuông tại H, ta có:

    ⦁ sinHAC^=CHAC

    Suy ra AC=CHsinHAC^=6sin60°=632=123=1233=43 (cm).

    ⦁ AH=AC⋅cosHAC^=43⋅cos60°=43⋅12=23.

    Xét ∆AHB vuông tại H, theo định lý Pythagore ta có:

    AB2=AH2+HB2=232+32=21

    Suy ra AB=21=4,582575695... cm≈5 cm.

    – Ta có: HAC^+HCA^=90°(tổng hai góc nhọn của ∆AHC vuông tại H).

    Suy ra HCA^=90°−HAC^=90°−60°=30°. Hay BCA^=30°.

    Xét ∆AHB vuông tại H, ta có:

    tanHBA^=AHHB=233, suy ra HBA^≈49°.

    Xét ∆ABC, ta có: BAC^+ACB^+ABC^=180° (định lý tổng ba góc trong tam giác)

    Suy ra BAC ^ =180°−CAB^−CBA^≈180°−30°−49°=101°.

    Xem thêm lời giải bài tập Toán 9 sách Kết nối tri thức hay, chi tiết khác:

    Bài 4.14 trang 80 Toán 9 Tập 1: Một cuốn sách khổ 17 × 24 cm, tức là chiều rộng 17 cm,...

    Bài 4.15 trang 80 Toán 9 Tập 1: Cho tam giác ABC có chân đường cao AH nằm giữa B và C....

    Bài 4.16 trang 80 Toán 9 Tập 1: Tìm chiều rộng d của dòng sông trong Hình 4.27 (làm tròn đến m)....

    Bài 4.17 trang 80 Toán 9 Tập 1: Tính các số liệu còn thiếu (dấu "?") ở Hình 4.28 với góc...

    Bài 4.18 trang 80 Toán 9 Tập 1: Một bạn muốn tính khoảng cách giữa hai địa điểm A, B ở hai bên hồ nước...

    Bài 4.19 trang 80 Toán 9 Tập 1: Mặt cắt ngang của một đập ngăn nước có dạng hình thang ABCD (H.4.30)...

    Bài 4.20 trang 80 Toán 9 Tập 1: Trong một buổi tập trận, một tàu ngầm đang ở trên mặt biển bắt đầu di chuyển...

    Xem thêm lời giải bài tập Toán 9 sách Kết nối tri thức hay, chi tiết khác:

    Bài 10: Căn bậc ba và căn thức bậc ba

    Luyện tập chung trang 63

    Bài tập cuối chương 3 trang 65

    Bài 11: Tỉ số lượng giác của góc nhọn

    Bài tập cuối chương 4 trang 81

    Tham khảo các loạt bài Toán 9 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,560 20/04/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: