Nội dung bài viết

    Xem thêm

    Cho hàm số y = tanx với x thuộc (-3pi/2; -pi/2) hợp (-pi/2; pi/2)

    Lời giải Bài 5 trang 27 SBT Toán 11 Tập 1 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11.

    1 1,143 06/11/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 11 Bài 4: Hàm số lượng giác và đồ thị

    Bài 5 trang 27 SBT Toán 11 Tập 1: Cho hàm số y = tanx với x∈(−3π2;−π2)∪(−π2;π2).

    a) Vẽ đồ thị hàm số đã cho.

    b) Tìm các giá trị của x∈[−7π4;π4] sao cho √3tan(x+π4)+1=0.

    c) Tìm các giá trị của x∈[−5π6;π6] sao cho tan(2x+π6)≥−√33.

    Lời giải:

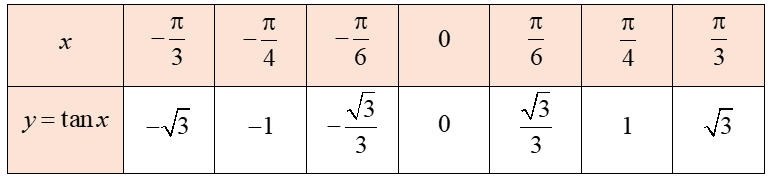
    a) Ta có bảng giá trị của hàm số y = tanx trên đoạn [−π3;π3] như sau:

    Cho hàm số y = tanx trang 27 SBT Toán 11 Tập 1

    Bằng cách tương tự, lấy nhiều điểm M(x; tanx) với x∈(−π2;π2) và nối lại, ta được đồ thị của hàm số y = tanx trên khoảng (−π2;π2).

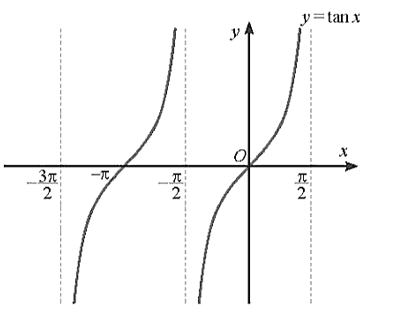
    Vì hàm số y = tanx tuần hoàn với chu kì π, nên để vẽ đồ thị hàm số y = tanx trên (−3π2;−π2)∪(−π2;π2), ta vẽ đồ thị của hàm số trên khoảng (−π2;π2), sau đó lặp lại đồ thị trên khoảng này trên (−3π2;−π2).

    Ta có đồ thị của hàm số y=tanx với x∈(−3π2;−π2)∪(−π2;π2) như sau:

    Cho hàm số y = tanx trang 27 SBT Toán 11 Tập 1

    b) Ta có √3tan(x+π4)+1=0 khi và chỉ khi tan(x+π4)=−√33.

    Đặt t=x+π4. Vì −7π4≤x≤π4 nên −3π2≤t≤π2, hay t∈[−3π2;π2].

    Hàm số y = tant xác định khi t≠π2+kπ,k∈ℤ.

    Kết hợp với điều kiện t∈[−3π2;π2], suy ra t∈(−3π2;−π2)∪(−π2;π2).

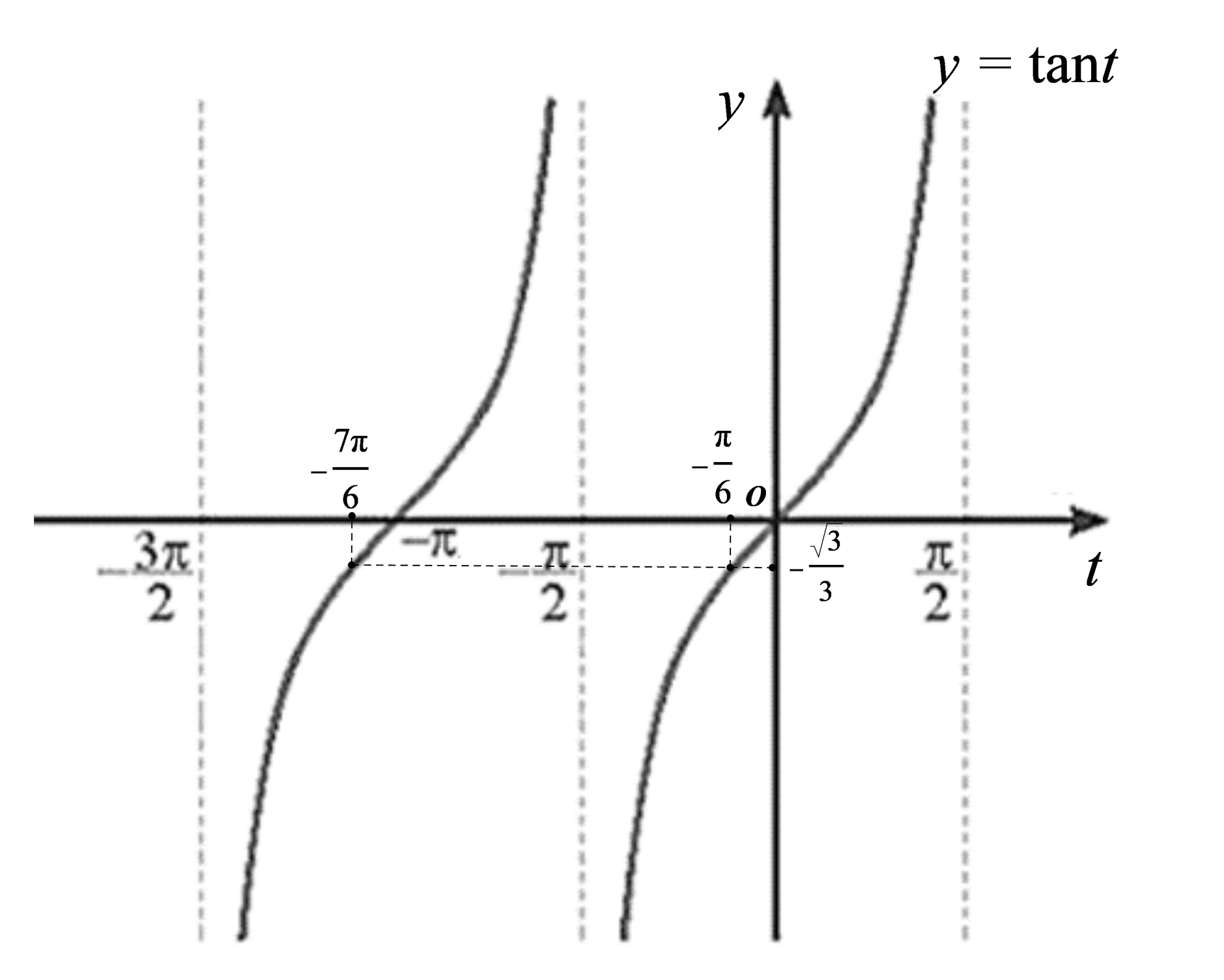
    Đồ thị hàm số y = tant với t∈(−3π2;−π2)∪(−π2;π2) như sau:

    Cho hàm số y = tanx trang 27 SBT Toán 11 Tập 1

    Từ đồ thị hàm số trên, ta có:

    tant=−√33 khi và chỉ khi t=−7π6 hoặc t=−π6.

    Hay x+π4=−7π6 hoặc x+π4=−π6

    Do đó x=−17π12 hoặc x=−5π12.

    c) Đặt t=2x+π6. Vì −5π6≤x≤π6 nên −3π2≤t≤π2, hay t∈[−3π2;π2].

    Tương tự câu b, từ đồ thị hàm số trên, ta có:

    tant≥−√33 khi và chỉ khi −7π6≤t<−π2 hoặc −π6≤t<π2.

    Hay −7π6≤2x+π6<−π2 hoặc −π6≤2x+π6<π2

    Do đó −2π3≤x<−π3 hoặc −π6≤x<π6.

    Xem thêm lời giải SBT Toán lớp 11 bộ sách Chân trời sáng tạo hay, chi tiết khác:

    Bài 1 trang 26 SBT Toán 11 Tập 1: Tìm tập xác định của các hàm số sau: a) y=−2sin3x;...

    Bài 2 trang 26 SBT Toán 11 Tập 1: Xét tính chẵn, lẻ của các hàm số sau: a) y=sin3xx;...

    Bài 3 trang 26 SBT Toán 11 Tập 1: Tìm tập giá trị của các hàm số sau: a) y=5−2cos(π3−x);...

    Bài 4 trang 27 SBT Toán 11 Tập 1: Cho hàm số y = sinx với x ∈ [‒2π; 2π]...

    Bài 5 trang 27 SBT Toán 11 Tập 1: Cho hàm số y = tanx với x∈(−3π2;−π2)∪(−π2;π2)....

    Bài 6 trang 27 SBT Toán 11 Tập 1: Chứng minh rằng các hàm số dưới đây là hàm số tuần hoàn....

    Bài 7 trang 27 SBT Toán 11 Tập 1: Huyết áp là áp lực máu cần thiết tác động lên thành động mạch nhằm đưa máu đi...

    Bài 8 trang 27 SBT Toán 11 Tập 1: Một chất điểm dao động điều hòa theo phương trình...

    Xem thêm lời giải SBT Toán lớp 11 bộ sách Chân trời sáng tạo hay, chi tiết khác:

    Bài 1: Góc lượng giác

    Bài 2: Giá trị lượng giác của một góc lượng giác

    Bài 3: Các công thức lượng giác

    Bài 5: Phương trình lượng giác cơ bản

    Bài tập cuối chương 1 trang 32

    Tham khảo các loạt bài Toán 11 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,143 06/11/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: