Nội dung bài viết

    Xem thêm

    Bài 5 trang 82 Toán 8 Tập 2 | Cánh diều Giải Toán lớp 8

    Lời giải Bài 5 trang 82 Toán 8 Tập 2 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8.

    1 343 29/12/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác

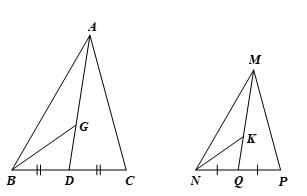
    Bài 5 trang 82 Toán 8 Tập 2: Cho ∆ABC ᔕ ∆MNP.

    a) Gọi D và Q lần lượt là trung điểm của BC và NP. Chứng minh ∆ABD ᔕ ∆MNQ.

    b) Gọi G và K lần lượt là trọng tâm của hai tam giác ABC và MNP. Chứng minh ∆ABG ᔕ ∆MNK.

    Lời giải:

    Bài 5 trang 82 Toán 8 Tập 2 Cánh diều | Giải Toán 8

    a) Vì ∆ABC ᔕ ∆MNP (giả thiết) nên ABC^=MNP^ và ABMN=BCNP

    Vì D, Q lần lượt là trung điểm của BC và NP nên BD=12BC,  NQ=12NP

    Do đó BDNQ=12BC12NP=BCNQ, suy ra ABMN=BDNQ  =BCNP

    Xét ∆ABDvà ∆MNQ có:

    ABD^=MNQ^ (do ABC^=MNP^);

    ABMN=BDNQ

    Suy ra ∆ABD ᔕ ∆MNQ (c.g.c).

    b) Vì ∆ABD ᔕ ∆MNQ (câu a) BAD^=NMQ^ (hai góc tương ứng) và ABMN=ADMQ (tỉ số đồng dạng)

    Mà G, K lần lượt là trọng tâm của hai tam giác ABC và MNP nên AG=23AD,  MK=23MQ

    Do đó ABMN=ADMQ=23AD23MQ=AGMK

    Xét ∆ABG và ∆MNK có:

    BAG^=NMK^ (do BAD^=NMQ^);

    ABMN=AGMK

    Vậy ∆ABG ᔕ ∆MNK (c.g.c).

    Xem thêm Lời giải bài tập Toán 8 Cánh diều hay, chi tiết khác: 

    Khởi động trang 79 Toán 8 Tập 2: Bạn Hoàng và bạn Thu cùng vẽ bản đồ một ốc đảo và ba vị trí với tỉ lệ bản đồ khác nhau. Bạn Hoàng dùng ba điểm A, B, C lần lượt biểu thị các vị trí...

    Hoạt động 1 trang 79 Toán 8 Tập 2: Quan sát Hình 68 và so sánh: a) Các tỉ số A'B'AB và A'C'AC; b) Các góc A^ và A'^...

    Luyện tập 1 trang 80 Toán 8 Tập 2: Cho hai tam giác ABC và A’B’C’ thoả mãn AB = 2, AC = 3, A’B’ = 6, A’C’ = 9 và A^=A'^. Chứng minh B^=B'^,  C^=C'^...

    Luyện tập 2 trang 80 Toán 8 Tập 2: Cho góc xOy. Trên tia Ox lấy các điểm A, B sao cho OA = 2cm, OB = 9cm. Trên tia Oy lấy các điểm M, Nsao cho OM = 3cm, ON = 6cm...

    Hoạt động 2 trang 81 Toán 8 Tập 2: Cho hai tam giác ABC và A’B’C’ có:A'^=A^=90°,  A'B'AB=A'C'AC(Hình 72). Chứng minh ∆A’B’C’ ᔕ ∆ABC...

    Luyện tập 3 trang 81 Toán 8 Tập 2: Cho hai tam giác ABC và A’B’C’ lần lượt vuông tại A và A’ sao cho ABAC=A'B'A'C'. Chứng minh B^=B'^...

    Bài 1 trang 81 Toán 8 Tập 2: Cho Hình 74. a) Chứng minh ∆ABC ᔕ ∆MNP. b) Góc nào của tam giác ∆MNP bằng góc B? c) Góc nào của tam giác ∆ABC bằng góc P...

    Bài 2 trang 82 Toán 8 Tập 2: Cho Hình 75, chứng minh: a) ∆IAB ᔕ ∆IDC; b) ∆IAD ᔕ ∆IBC...

    Bài 3 trang 82 Toán 8 Tập 2: Cho Hình 76, biết AB = 4, BC = 3, BE = 2, BD = 6. Chứng minh: a) ∆ABD ᔕ ∆EBC; b) DAB^=DEG^; c) Tam giác DGE vuông...

    Bài 4 trang 82 Toán 8 Tập 2: Cho Hình 77, chứng minh: a) ABC^=BED^; b) BC ⊥ BE...

    Bài 5 trang 82 Toán 8 Tập 2: Cho ∆ABC ᔕ ∆MNP. a) Gọi D và Q lần lượt là trung điểm của BC và NP. Chứng minh ∆ABD ᔕ ∆MNQ...

    Bài 6 trang 82 Toán 8 Tập 2: Cho Hình 78, biết AH2 = BH.CH. Chứng minh: a) ∆HAB ᔕ ∆HCA; b) Tam giác ∆ABC vuông tại A...

    Bài 7 trang 82 Toán 8 Tập 2: Đố. Chỉ sử dụng thước thẳng có chia đơn vị đến milimét và thước đo góc, làm thế nào đo được khoảng cách giữa hai vị trí B, C trên thực tế...

    Xem thêm Lời giải bài tập Toán 8 Cánh diều hay, chi tiết khác: 

    Bài 6: Trường hợp đồng dạng thứ nhất của tam giác

    Bài 8: Trường hợp đồng dạng thứ ba của tam giác

    Bài 9: Hình đồng dạng

    Bài 10: Hình đồng dạng trong thực tiễn

    Bài tập cuối chương 8 trang 94

    Tham khảo các loạt bài Toán 8 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 343 29/12/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: