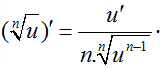Trong các hàm số sau, hàm số đồng biến trên tập xác định của nó là: y=log (căn3 /2) của x
Lời giải Bài 39 trang 44 SBT Toán 11 Tập 2 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11.
Giải SBT Toán 11 Bài 3: Hàm số mũ. Hàm số lôgarit
Bài 39 trang 44 SBT Toán 11 Tập 2: Trong các hàm số sau, hàm số đồng biến trên tập xác định của nó là:
A. y=log√32x.
B. y = log0,5 x;
C. y = – logx;
D. y = lnx.
Đáp án đúng là: D
* Lời giải:
Cả 4 đáp án đều có tập xác định: D = (0; +∞).
Do e > 1 nên hàm số y = lnx đồng biến trên D = (0; +∞) hay hàm số y = lnx đồng biến trên tập xác định của nó.
* Phương pháp giải:
- Hàm số log cơ số a > 1 thì đồng biến; < 1 là nghịch biến
+ Nên đáp án A, B đều < 1 nên sẽ nghịch biến
+ Đáp án C là giá trị âm nên không thể đồng biến
* Lý thuyết
HÀM SỐ LOGARIT:
Định nghĩa logarit
Cho hai số dương a; b với a ≠ 1. Số α thỏa mãn đẳng thức aα = b được gọi là logarit cơ số a của b và kí hiệu là logab.
α = logab ⇔aα = b
– Chú ý: Không có logarit của số âm và số 0.
Tính chất của logarit
Cho hai số dương a và b; a ≠ 1. Ta có các tính chất sau đây:
loga1 = 0; logaa = 1
alogab =b; log a(aα) = α
Quy tắc tính logarit
Logarit của một tích
– Định lí 1. Cho ba số dương a; b1 ;b2 với a ≠ 1. Ta có:
loga (b1.b)2 = logab1+ logab2
Logarit của một tích bằng tổng các logarit.
– Chú ý:
Định lí 1 có thể mở rộng cho tích n số dương:
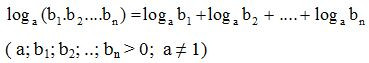
Logarit của một thương
– Định lí 2. Cho ba số dương a; b1 ;b2 với a ≠ 1. Ta có:
loga b1b2 = logab1− logab2
Logarit của một thương bằng hiệu các logarit.
Đặc biệt: loga 1b = −logab( a > 0; b > 0; a ≠ 1)
Logarit của một lũy thừa
– Định lí 3. Cho hai số dương a; b và a ≠ 1 . Với mọi số α, ta có:
logabα = αlogab
Logarit của một lũy thừa bằng tích của số mũ với logarit của cơ số.
– Đặc biệt: logan√b = 1n logab
Đổi cơ số logarit
– Định lí 4. Cho ba số dương a; b; c với a ≠ 1; c ≠ 1, ta có:
logab = logcblogca
– Đặc biệt:
logab = 1logba (b≠1)logaαb = 1αlogab (α≠0)
Logarit thập phân. Logarit tự nhiên
Logarit thập phân
Logarit thập phân là logarit cơ số 10.
log10b thường được viết là logb hoặc lgb.
Logarit tự nhiên
– Logarit tự nhiên là logarit cơ số e. Logeb được viết là lnb.
HÀM SỐ MŨ: y = ax, (a > 0, a ≠ 1)
Tập xác định: D = R
Tập giá trị: T = (); +∝), nghĩa là khi giải phương trình mũ mà đặt t = af(x) thì t > 0
Tính đơn điệu:
+ Khi a > 1 thì hàm số y = ax đồng biến, khi đó ta luôn có: af(x) > ag(x) ⇔ f(x) > g(x).
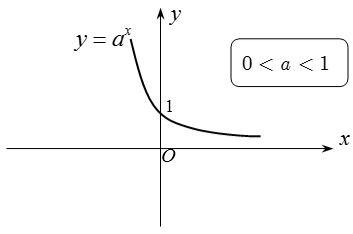
+ Khi 0 < a < 1 thì hàm số y = ax nghịch biến, khi đó ta luôn có: af(x) > ag(x) ⇔ f(x) < g(x).
Đạo hàm:
(ax)' = ax.ln a ⇒ (au)' = u'.au.ln a
(ex)' = ex ⇒ (eu)' = eu.u'
Đồ thị: Nhận trục hoành làm đường tiệm cận ngang.
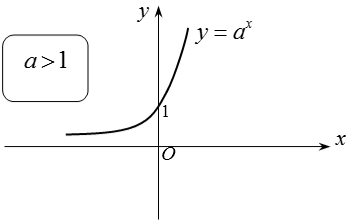
Xem thêm các bài viết liên quan hay, chi tiết
Hàm số mũ và hàm số lôgarit | Lý thuyết, công thức, các dạng bài tập và cách giải
Toán 12 Bài 4: Hàm số mũ. Hàm số lôgarit
50 Bài tập Lôgarit Toán 12 mới nhất
Xem thêm lời giải SBT Toán lớp 11 bộ sách Cánh diều hay, chi tiết khác:
Bài 34 trang 44 SBT Toán 11 Tập 2: Tập xác định của hàm số y = 0,2x – 1 là:...
Bài 35 trang 44 SBT Toán 11 Tập 2: Tập xác định của hàm số y = log3(2x + 1) là:...
Bài 36 trang 44 SBT Toán 11 Tập 2: Tập xác định của hàm số y = log5(x2) là:...
Bài 37 trang 44 SBT Toán 11 Tập 2: Trong các hàm số sau, hàm số có tập xác định ℝ là:...
Bài 41 trang 44 SBT Toán 11 Tập 2: Cho a73<a78logb(√2+√5)<logb(√2+√3). Kết luận nào sau đây đúng?...
Bài 42 trang 45 SBT Toán 11 Tập 2: Đường nào sau đây là đồ thị hàm số y = 4x?....
Bài 43 trang 45 SBT Toán 11 Tập 2: Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số lôgarit...
Bài 44 trang 45 SBT Toán 11 Tập 2: Lập bảng biến thiên và vẽ đồ thị hàm số:...
Bài 47 trang 46 SBT Toán 11 Tập 2: Tìm tập xác định của các hàm số:...
Bài 50 trang 46 SBT Toán 11 Tập 2: Cho hàm số: f(x)=9x9x+3....
Bài 51 trang 46 SBT Toán 11 Tập 2: Các nhà khoa học xác định được chu kì...
Bài 52 trang 46 SBT Toán 11 Tập 2: Mức cường độ âm L (dB) được tính...
Xem thêm lời giải SBT Toán lớp 11 bộ sách Cánh diều hay, chi tiết khác:
Bài 4: Phương trình, bất phương trình mũ và lôgarit
Bài 1: Định nghĩa đạo hàm. Ý nghĩa hình học của đạo hàm
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Cánh diều (hay nhất)
- Văn mẫu lớp 11 - Cánh diều
- Tóm tắt tác phẩm Ngữ văn 11 – Cánh diều
- Tác giả tác phẩm Ngữ văn 11 - Cánh diều
- Giải SBT Ngữ văn 11 – Cánh diều
- Bố cục tác phẩm Ngữ văn 11 – Cánh diều
- Giải Chuyên đề học tập Ngữ văn 11 – Cánh diều
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Cánh diều
- Soạn văn 11 Cánh diều (ngắn nhất)
- Giải sgk Tiếng Anh 11 – ilearn Smart World
- Giải sbt Tiếng Anh 11 - ilearn Smart World
- Trọn bộ Từ vựng Tiếng Anh 11 ilearn Smart World đầy đủ nhất
- Giải sgk Vật lí 11 – Cánh diều
- Lý thuyết Vật lí 11 – Cánh diều
- Giải sbt Vật lí 11 – Cánh diều
- Giải Chuyên đề học tập Vật lí 11 – Cánh diều
- Giải sgk Hóa học 11 – Cánh diều
- Giải Chuyên đề học tập Hóa học 11 – Cánh diều
- Lý thuyết Hóa 11 - Cánh diều
- Giải sbt Hóa học 11 – Cánh diều
- Giải sgk Sinh học 11 – Cánh diều
- Lý thuyết Sinh học 11 – Cánh diều
- Giải Chuyên đề học tập Sinh học 11 – Cánh diều
- Giải sbt Sinh học 11 – Cánh diều
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Cánh diều
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Cánh diều
- Lý thuyết Kinh tế pháp luật 11 – Cánh diều
- Giải sbt Kinh tế pháp luật 11 – Cánh diều
- Giải sgk Lịch sử 11 – Cánh diều
- Giải Chuyên đề học tập Lịch sử 11 – Cánh diều
- Lý thuyết Lịch sử 11 - Cánh diều
- Giải sbt Lịch sử 11 – Cánh diều
- Giải sgk Địa lí 11 – Cánh diều
- Giải Chuyên đề học tập Địa lí 11 – Cánh diều
- Lý thuyết Địa lí 11 - Cánh diều
- Giải sbt Địa lí 11 – Cánh diều
- Giải sgk Công nghệ 11 – Cánh diều
- Lý thuyết Công nghệ 11 - Cánh diều
- Giải sbt Công nghệ 11 – Cánh diều
- Giải sgk Tin học 11 – Cánh diều
- Giải Chuyên đề học tập Tin học 11 – Cánh diều
- Lý thuyết Tin học 11 - Cánh diều
- Giải sbt Tin học 11 – Cánh diều
- Giải sgk Giáo dục quốc phòng an ninh 11 – Cánh diều
- Lý thuyết Giáo dục quốc phòng 11 – Cánh diều
- Giải sbt Giáo dục quốc phòng 11 – Cánh diều
- Giải sgk Hoạt động trải nghiệm 11 – Cánh diều