Nội dung bài viết

    Xem thêm

    Hoạt động khám phá 2 trang 8 Toán Tập 2 | Chân trời sáng tạo Giải Toán lớp 10

    Lời giải Hoạt động khám phá 2 trang 8 Toán lớp 10 Tập 2 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 10.

    1 317 03/03/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SGK Toán 10 Chân trời sáng tạo Bài 1: Dấu của tam thức bậc hai

    Hoạt động khám phá 2 trang 8 Toán lớp 10 Tập 2: Quan sát đồ thị của các hàm số bậc hai trong các hình dưới đây. Trong mỗi trường hợp hãy cho biết:

    - Các nghiệm (nếu có) và dấu của biệt thức ∆.

    - Các khoảng giá trị của x mà trên đó f(x) cùng dấu với hệ số của x2.

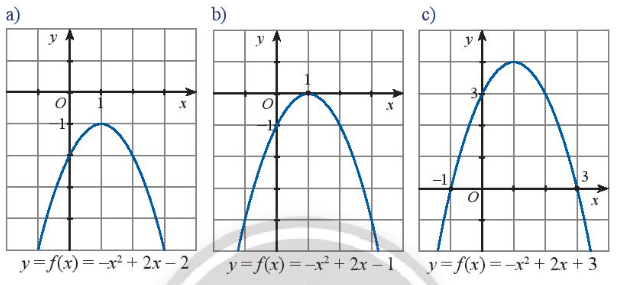
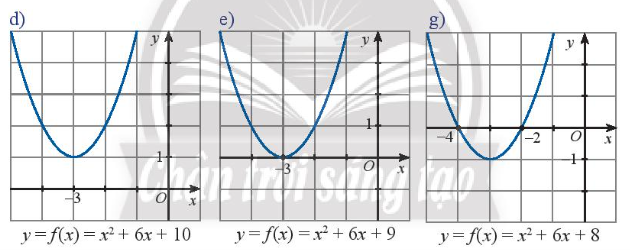
    Giải Toán 10 Bài 1 (Chân trời sáng tạo): Dấu của tam thức bậc hai (ảnh 1)

    Giải Toán 10 Bài 1 (Chân trời sáng tạo): Dấu của tam thức bậc hai (ảnh 1)

    Lời giải:

    a) Dựa vào hình vẽ ta thấy đồ thị hàm số không cắt trục hoành nên tam thức f(x) = - x2 + 2x – 2 vô nghiệm.

    Ta có ∆ = 22 – 4(-1).(-2) = 4 – 8 = - 4 < 0.

    Tam thức f(x) có hệ số a = -1 < 0.

    Ta thấy toàn bộ đồ thị hàm số nằm phía dưới trục hoành nên f(x) < 0 với mọi x.

    Suy ra f(x) cùng dấu với hệ số a với mọi x.

    b) Dựa vào hình vẽ ta thấy đồ thị hàm số cắt trục hoành tại một điểm duy nhất có hoành độ x = 1 nên tam thức f(x) = - x2 + 2x – 1 có một nghiệm duy nhất x = 1.

    Ta có ∆ = 22 – 4(-1).(-1) = 4 – 4 = 0.

    Tam thức f(x) có hệ số a = -1 < 0.

    Ta thấy với x ≠ 1 toàn bộ đồ thị hàm số nằm phía dưới trục hoành nên f(x) < 0 với x ≠ 1 và f(x) = 0 với x = 1.

    Suy ra f(x) cùng dấu với hệ số a với x ≠ 1.

    c) Dựa vào hình vẽ ta thấy đồ thị hàm số cắt trục hoành tại hai điểm phân biệt có hoành độ lần lượt là x1 = - 1 và x2 = 3 nên tam thức f(x) = - x2 + 2x + 3 có hai nghiệm phân biệt x1 = - 1 và x2 = 3.

    Ta có ∆ = 22 – 4.3.(-1) = 4 + 12 = 16 > 0.

    Tam thức f(x) có hệ số a = -1 < 0.

    Ta thấy với x < - 1 hoặc x > 3 thì đồ thị hàm số nằm phía dưới trục hoành, với -1 < x < 3 thì đồ thị hàm số nằm phía trên trục hoành hay f(x) < 0 với x < -1 hoặc x > 3; f(x) > 0 với -1 < x < 3 và f(x) = 0 tại x = -1 hoặc x = 3.

    Suy ra f(x) cùng dấu với hệ số a với x < -1 hoặc x > 3.

    d) Dựa vào hình vẽ ta thấy đồ thị hàm số không cắt trục hoành nên tam thức f(x) = x2 + 6x + 10 vô nghiệm.

    Ta có ∆ = 62 – 4.1.10 = 36 – 40 = - 4 < 0.

    Tam thức f(x) có hệ số a = 1 > 0.

    Ta thấy toàn bộ đồ thị hàm số nằm phía trên trục hoành nên f(x) > 0 với mọi x.

    Suy ra f(x) cùng dấu với hệ số a với mọi x.

    e) Dựa vào hình vẽ ta thấy đồ thị hàm số cắt trục hoành tại một điểm duy nhất có hoành độ x = -3 nên tam thức f(x) = x2 + 6x + 9 có một nghiệm duy nhất x = -3.

    Ta có ∆ = 62 – 4.1.9 = 36 – 36 = 0.

    Tam thức f(x) có hệ số a = 1 > 0.

    Ta thấy với x ≠ -3 toàn bộ đồ thị hàm số nằm phía trên trục hoành nên f(x) > 0 với x ≠ - 3 và f(x) = 0 với x = -3.

    Suy ra f(x) cùng dấu với hệ số a với x ≠ -3.

    g) Dựa vào hình vẽ ta thấy đồ thị hàm số cắt trục hoành tại hai điểm phân biệt có hoành độ lần lượt là x1 = -4 và x2 = -2 nên tam thức f(x) = x2 + 6x + 8 có hai nghiệm phân biệt x1 = -4 và x2 = -2.

    Ta có ∆ = 62 – 4.1.8 = 36 – 32 = 4 > 0.

    Tam thức f(x) có hệ số a = 1 > 0.

    Ta thấy với x < - 4 hoặc x > -2 thì đồ thị hàm số nằm phía trên trục hoành, với -4 < x < -2 thì đồ thị hàm số nằm phía dưới trục hoành hay f(x) > 0 với x < -4 hoặc x > 2; f(x) < 0 với -4 < x < -2 và f(x) = 0 tại x = -4 hoặc x = -2.

    Suy ra f(x) cùng dấu với hệ số a với x < -4 hoặc x > -2.

    Xem thêm các bài giải sách giáo khoa Toán 10 bộ sách Chân trời sáng tạo hay, chi tiết khác:

    Hoạt động khởi động trang 6 Toán lớp 10 Tập 2: Cầu vòm được thiết kế với thanh vòm hình parabol và mặt cầu... 

    Hoạt động khám phá 1 trang 6 Toán lớp 10 Tập 2: Đồ thị của hàm số y = f(x) = - x2 + x + 3 được biểu diễn trong Hình 1... 

    Thực hành 1 trang 7 Toán lớp 10 Tập 2: Biểu thức nào sau đây là tam thức bậc hai? Nếu là tam... 

    Thực hành 1 trang 7 Toán lớp 10 Tập 2: Tìm biệt thức và nghiệm của tam thức bậc hai sau:... 

    Thực hành 3 trang 9 Toán lớp 10 Tập 2: Xét dấu của tam thức bậc hai sau:... 

    Vận dụng trang 9 Toán lớp 10 Tập 2: Xét dấu tam thức bậc hai h(x) = -0,006x2 + 1,2x – 30... 

    Bài 1 trang 9 Toán lớp 10 Tập 2: Đa thức nào sau đây là tam thức bậc hai?... 

    Bài 2 trang 9 Toán lớp 10 Tập 2: Xác định giá trị của m để đa thức sau là tam thức bậc hai... 

    Bài 3 trang 10 Toán lớp 10 Tập 2: Dựa vào đồ thị của các hàm số bậc hai sau đây, hãy lập bảng... 

    Bài 4 trang 10 Toán lớp 10 Tập 2: Xét dấu của tam thức bậc hai sau đây:... 

    Bài 5 trang 10 Toán lớp 10 Tập 2: Độ cao (tính bằng mét) của một quả bóng so với vành rổ khi... 

    Bài 6 trang 10 Toán lớp 10 Tập 2: Một khung dây thép hình chữ nhật có chiều dài 20 cm và... 

    Bài 7 trang 10 Toán lớp 10 Tập 2: Chứng minh rằng với mọi số thực m ta luôn có 9m2 + 2m... 

    Bài 8 trang 10 Toán lớp 10 Tập 2: Tìm giá trị của m để:... 

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 317 03/03/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: