Giải Toán 9 trang 82 Tập 1 Kết nối tri thức
Với giải bài tập Toán lớp 9 trang 82 trong Bài tập cuối chương 4 trang 81 sách Kết nối tri thức Tập 1 hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán lớp 9 trang 82 Tập 1.
Giải Toán 9 trang 82 Tập 1
Lời giải:
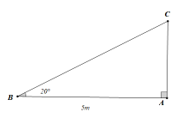
Giả sử hình ảnh cây bị gãy mô tả bởi hình vẽ như dưới đây:
Xét ∆ABC vuông tại A, ta có:
⦁ AC = AB.tan20° = 5.tan20° ≈ 1,8 (m);
⦁ suy ra
Khi đó: AC + CB ≈ 1,8 + 5,3 = 7,1 (m).
Vậy trước khi bị gãy, cây cao khoảng 7,1 m.
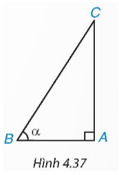
Bài 4.29 trang 82 Toán 9 Tập 1: Cho tam giác ABC vuông tại A, có (H.4.37).
a) Hãy viết các tỉ số lượng giác sinα, cosα.
b) Sử dụng định lí Pythagore, chứng minh rằng sin2α + cos2α = 1.
Lời giải:
a) Theo định nghĩa tỉ số lượng giác sin và cos, ta có:
và
b) Ta có:
Áp dụng định lí Pythagore cho ∆ABC vuông tại A, ta có: BC2 = AB2 + AC2
Do đó:
Vậy sin2α + cos2α = 1.
Bài 4.30 trang 82 Toán 9 Tập 1: ĐỐ VUI. Chu vi Trái Đất bằng bao nhiêu?
2. Cũng vào trưa một ngày Hạ chí, ở thành phố Alexandria (A-lếch-xăng-đri-a) cách Syene 800 km, Eratosthenes thấy một tháp cao 25 m có bóng trên mặt đất dài 3,1 m.
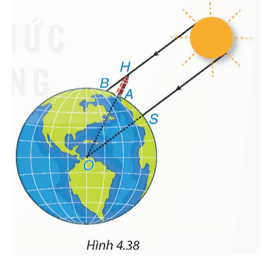
Từ hai quan sát trên, ông có thể tính xấp xỉ "chu vi" của Trái Đất như thế nào? (trên Hình 4.38, điểm O là tâm Trái Đất, điểm S tượng trưng cho thành phố Syene, điểm A tượng trưng cho thành phố Alexandria, điểm H là đỉnh của tháp, bóng của tháp trên mặt đất được coi là đoạn thẳng AB).
Lời giải:
Theo em, nhà toán học và thiên văn học Eratosthenes đã tính xấp xỉ "chu vi" của Trái Đất như sau:
Các tia sáng mặt trời chiếu thẳng đứng, nên ta coi các tia sáng BH, OS song song với nhau. Khi đó (hai góc so le trong).
Xét ∆ABH vuông tại A, ta có:
suy ra Do đó
Xét ∆OAS vuông tại S, ta có:
suy ra
Khi đó, “chu vi” của Trái Đất khoảng:
2π.OA ≈ 2 . 3,14 . 6 502,79 ≈ 40 838 (km).
Xem thêm lời giải bài tập Toán 9 sách Kết nối tri thức hay, chi tiết khác:
Xem thêm lời giải bài tập Toán 9 sách Kết nối tri thức hay, chi tiết khác:
Bài 4.21 trang 81 Toán 9 Tập 1: Trong Hình 4.32, cosα bằng...
Bài 4.22 trang 81 Toán 9 Tập 1: Trong tam giác MNP vuông tại M...
Bài 4.23 trang 81 Toán 9 Tập 1: Trong tam giác ABC vuông tại A (H.4.34),...
Bài 4.24 trang 81 Toán 9 Tập 1: Với mọi góc nhọn α, ta có...
Bài 4.25 trang 81 Toán 9 Tập 1: Giá trị tan30° bằng...
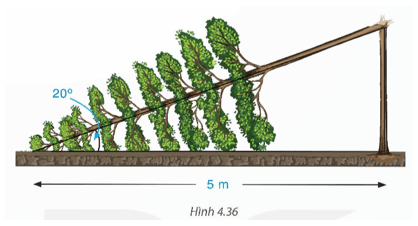
Bài 4.28 trang 82 Toán 9 Tập 1: Một cây cao bị gãy, ngọn cây đổ xuống mặt đất. Ba điểm: gốc cây,...
Bài 4.29 trang 82 Toán 9 Tập 1: Cho tam giác ABC vuông tại A, có (H.4.37)....
Bài 4.30 trang 82 Toán 9 Tập 1: ĐỐ VUI. Chu vi Trái Đất bằng bao nhiêu?...
Xem thêm lời giải bài tập Toán 9 sách Kết nối tri thức hay, chi tiết khác:
Bài tập cuối chương 3 trang 65
Bài 11: Tỉ số lượng giác của góc nhọn
Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng
Xem thêm các chương trình khác:
- Soạn văn 9 Kết nối tri thức (hay nhất)
- Văn mẫu 9 - Kết nối tri thức
- Tóm tắt tác phẩm Ngữ văn 9 – Kết nối tri thức
- Tác giả tác phẩm Ngữ văn 9 - Kết nối tri thức
- Bố cục tác phẩm Ngữ văn 9 – Kết nối tri thức
- Nội dung chính tác phẩm Ngữ văn 9 – Kết nối tri thức
- Soạn văn 9 Kết nối tri thức (ngắn nhất)
- Bài tập Tiếng Anh 9 Global success theo Unit có đáp án
- Giải sgk Tiếng Anh 9 - Global success
- Trọn bộ Từ vựng Tiếng Anh 9 Global success đầy đủ nhất
- Trọn bộ Ngữ pháp Tiếng Anh 9 Global success đầy đủ nhất
- Giải sbt Tiếng Anh 9 – Global Success
- Giải sgk Khoa học tự nhiên 9 – Kết nối tri thức
- Lý thuyết Khoa học tự nhiên 9 – Kết nối tri thức
- Giải sbt Khoa học tự nhiên 9 – Kết nối tri thức
- Giải sgk Lịch sử 9 – Kết nối tri thức
- Giải sbt Lịch sử 9 – Kết nối tri thức
- Giải sgk Địa lí 9 – Kết nối tri thức
- Giải sbt Địa lí 9 – Kết nối tri thức
- Giải sgk Tin học 9 – Kết nối tri thức
- Giải sbt Tin học 9 – Kết nối tri thức
- Giải sgk Công nghệ 9 – Kết nối tri thức
- Giải sgk Giáo dục công dân 9 – Kết nối tri thức
- Giải sbt Giáo dục công dân 9 – Kết nối tri thức
- Giải sgk Hoạt động trải nghiệm 9 – Kết nối tri thức