Giải Toán 8 trang 67 Tập 2 Chân trời sáng tạo

Với giải bài tập Toán 8 trang 67 Tập 2 trong Bài 2: Các trường hợp đồng dạng của hai tam giác sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 8 trang 67 Tập 2.

1 101 28/12/2023

Trang trước

Trang sau

Giải Toán 8 trang 67 Tập 2

Khởi động trang 67 Toán 8 Tập 2: Các trường hợp đồng dạng của hai tam giác có điều gì khác với các trường hợp bằng nhau của hai tam giác?

Lời giải:

Sau bài học này, ta giải quyết bài toán trên như sau:

Trường hợp	Giống nhau	Khác nhau
Trường hợp	Giống nhau	Bằng nhau	Đồng dạng
1	3 cạnh	3 cạnh tương ứng bằng nhau	3 cạnh tương ứng tỉ lệ
2	2 cạnh 1 góc	2 cạnh tương ứng và một góc kề với hai cạnh bằng nhau	2 cạnh tương ứng tỉ lệ
3	2 góc bằng nhau	1 cạnh và 2 góc kề tương ứng bằng nhau	Chỉ 2 góc bằng nhau, không cần có điều kiện cạnh

1. Trường hợp đồng dạng thứ nhất (c.c.c)

Khám phá 1 trang 67 Toán 8 Tập 2: Cho tam giác ABC và tam giác A'B'C' có các kích thước như Hình 1. Trên cạnh AB và AC của tam giác ABC lần lượt lấy hai điểm M, N sao cho AM = 2 cm, AN = 3 cm.

a) So sánh các tỉ số $\frac{A' B'}{AB}, \frac{A' C'}{AC}, \frac{B' C'}{BC}$ .

b) Tính độ dài đoạn thẳng MN.

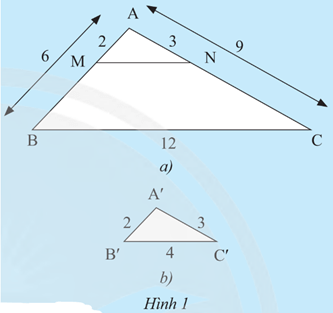
c) Em có nhận xét gì về mối quan hệ giữa các tam giác ABC, AMN và A'B'C'.

Lời giải:

a) Ta có: $\frac{A' B'}{AB} = \frac{2}{6} = \frac{1}{3}$ ;

$\frac{A' C'}{AC} = \frac{3}{9} = \frac{1}{3}$ ;

$\frac{B' C'}{BC} = \frac{4}{12} = \frac{1}{3}$ .

Do đó $\frac{A' B'}{AB} = \frac{B' C'}{BC} = \frac{A' C'}{AC} = \frac{1}{3}$ .

b) Tam giác ABC có $\frac{AM}{AB} = \frac{AN}{AC} = \frac{1}{3}$ , theo định lí Thalès đảo suy ra MN // BC.

Khi đó ΔAMN ᔕ ΔABC nên $\frac{AM}{AB} = \frac{AN}{AC} = \frac{MN}{BC} = \frac{1}{3}$ suy ra MN = 4.

c) Xét tam giác AMN và A'B'C' có:

• MN = B'C' = 4;

• AM = A'B' = 2;

• AN = A'C' = 3.

Suy ra ΔAMN = ΔA′B′C′ (c.c.c).

Nhận xét: ΔAMN = ΔA′B′C′, ΔA′B′C′ ᔕ ΔABC và ΔAMN ᔕ ΔABC.

Xem thêm Lời giải bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:

Giải Toán 8 trang 67 Tập 2

Giải Toán 8 trang 68 Tập 2

Giải Toán 8 trang 69 Tập 2

Giải Toán 8 trang 70 Tập 2

Giải Toán 8 trang 71 Tập 2

Giải Toán 8 trang 72 Tập 2

Xem thêm Lời giải bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:

Khởi động trang 67 Toán 8 Tập 2: Các trường hợp đồng dạng của hai tam giác có điều gì khác với các trường hợp bằng nhau của hai tam giác...

Khám phá 1 trang 67 Toán 8 Tập 2: Cho tam giác ABC và tam giác A'B'C' có các kích thước như Hình 1. Trên cạnh AB và AC của tam giác ABC lần lượt lấy hai điểm M, N...

Thực hành 1 trang 68 Toán 8 Tập 2: Tìm trong Hình 4 các cặp tam giác đồng dạng...

Khám phá 2 trang 68 Toán 8 Tập 2: Cho tam giác DEF và ABC có $DE = \frac{1}{3} AB, DF = \frac{1}{3} AC, \hat{D} = \hat{A}$ (Hình 5). Trên tia AB, lấy điểm M sao cho AM = DE...

Thực hành 2 trang 69 Toán 8 Tập 2: Cho tam giác ADE và tam giác ACF có các kích thước như trong Hình 8. Chứng minh rằng ΔADE ᔕ ΔACF...

Khám phá 3 trang 69 Toán 8 Tập 2: Cho hai tam giác ABC và A'B'C' có $\hat{A} = \hat{A'}, \hat{C} = \hat{C'}$ (Hình 9)...

Thực hành 3 trang 70 Toán 8 Tập 2: Quan sát Hình 12. a) Chứng minh rằng ΔABC ᔕ ΔA′B′C′. b) Tính độ dài B'C'...

Vận dụng 1 trang 70 Toán 8 Tập 2: Cho hình thang ABCD (AB // CD) có AB = 6 m, CD = 15 m, OD = 8 m (Hình 13). Tính độ dài đoạn thẳng OB...

Vận dụng 2 trang 70 Toán 8 Tập 2: Qua các trường hợp đồng dạng của hai tam giác, hãy trả lời câu hỏi ở Hoạt động khởi động (trang 67)...

Bài 1 trang 70 Toán 8 Tập 2: a) Tam giác AFE và MNG ở Hình 14 có đồng dạng với nhau không? Vì sao...

Bài 2 trang 70 Toán 8 Tập 2: Tam giác ABC có độ dài AB = 4 cm, AC = 6 cm, BC = 9 cm. Tam giác A'B'C' đồng dạng với tam giác ABC và có chu vi bằng 66,5 cm...

Bài 3 trang 70 Toán 8 Tập 2: Một công viên có hai đường chạy bộ hình tam giác đồng dạng như Hình 15. Kích thước của con đường bên trong lần lượt là 300 m, 350 m và 550 m...

Bài 4 trang 71 Toán 8 Tập 2: Xét xem cặp tam giác nào trong các Hình 16a, 16b đồng dạng...

Bài 5 trang 71 Toán 8 Tập 2: Trong Hình 17, cho biết DE = 6 cm, EF= 7,8 cm, NP = 13 cm, NM = 10 cm, $\hat{E} = \hat{N}$ và $\hat{P} = 42^{o}$ . Tính $\hat{F}$ ...

Bài 6 trang 71 Toán 8 Tập 2: a) Cho tam giác ABC có AB = 12 cm, AC = 15 cm, BC = 18 cm. Trên cạnh AB, lấy điểm E sao cho AE = 10 cm...

Bài 7 trang 71 Toán 8 Tập 2: Trong Hình 19, cho biết MN // BC, MB // AC. a) Chứng minh ΔBNM ᔕ ΔABC. b) Tính $\hat{C}$ ...

Bài 8 trang 72 Toán 8 Tập 2: a) Trong Hình 20a, cho biết $\hat{N} = \hat{E}, \hat{M} = \hat{D}$ , MP = 18 m, DF = 24 m, EF = 32 m, NP = a + 3 (m). Tìm a...

Bài 9 trang 72 Toán 8 Tập 2: a) Trong Hình 21a, cho biết $\hat{HOP} = \hat{HPE}, \hat{HPO} = \hat{HEP}$ , OH = 6 cm và HE = 4 cm. Tính độ dài đoạn thẳng HP...

Bài 10 trang 72 Toán 8 Tập 2: Đường đi và khoảng cách từ nhà anh Thanh (điểm M) đến công ty (điểm N) được thể hiện trong Hình 22...

Xem thêm Lời giải bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Hai tam giác đồng dạng

Bài 3: Các trường hợp đồng dạng của hai tam giác vuông

Bài 4: Hai hình đồng dạng

Bài tập cuối chương 8 trang 84

Bài 1: Mô tả xác suất bằng tỉ số

1 101 28/12/2023

Trang trước

Trang sau

Xem thêm các chương trình khác: