Giải Toán 11 trang 80 Tập 1 Chân trời sáng tạo
Với giải bài tập Toán 11 trang 80 trong Bài 3: Hàm số liên tục sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 11 trang 80.
Giải Toán 11 trang 80 Tập 1
Lời giải:
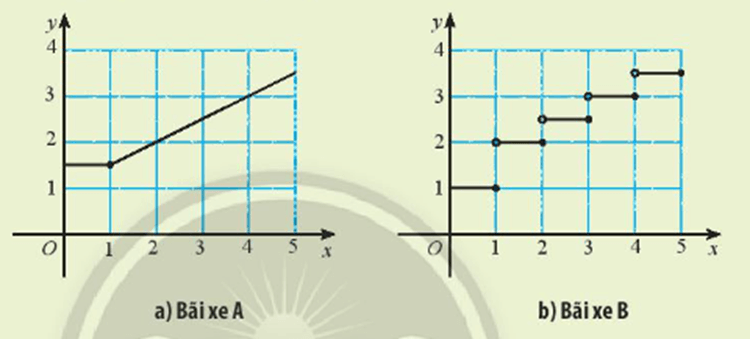
+) Bãi xe A:
Dựa vào đồ thị hàm số ta thấy, theo thời gian gửi x (giờ) tăng thì phí gửi xe tăng dần.
+) Bãi xe B:
Dựa vào đồ thị hàm số ta thấy, theo thời gian gửi x (giờ) tăng thì phí gửi xe tăng dần theo nấc.
1. Hàm số liên tục tại một điểm
Hoạt động khám phá 1 trang 80 Toán 11 Tập 1: Cho hàm số 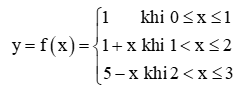
Tại mỗi điểm x0 = 1 và x0 = 2, có tồn tại giới hạn không? Nếu có, giới hạn đó có bằng f(x0) không?
Lời giải:
+) Tại x0 = 1 ta có:
Dãy (xn) bất kì thỏa mãn xn < 1 và xn → 1 thì f(xn) = 1 khi đó .
Dãy (xn) bất kì thỏa mãn 1 < xn ≤ 2 và xn → 1 thì f(xn) = 1 + xn khi đó .
Suy ra . Do đó không tồn tại .
+) Tại x0 = 2
Dãy (xn) bất kì thỏa mãn xn < 2 và xn → 2 thì f(xn) = 1 + xn khi đó .
Dãy (xn) bất kì thỏa mãn 2 < xn ≤ 3 và xn → 2 thì f(xn) = 5 – xn khi đó .
Suy ra . Do đó .
Ta có f(2) = 1 + 2 = 3.
Vì vậy .
Xem thêm lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Xem thêm lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Hoạt động khám phá 1 trang 80 Toán 11 Tập 1: Cho hàm số 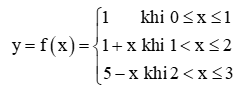
Thực hành 1 trang 81 Toán 11 Tập 1: Xét tính liên tục của hàm số: a) f(x) = 1 – x2 tại điểm x0 = 3;...
Hoạt động khám phá 2 trang 81 Toán 11 Tập 1: Cho hàm số
Thực hành 2 trang 82 Toán 11 Tập 1: Xét tính liên tục của hàm số: trên [1; 2]...
Hoạt động khám phá 3 trang 82 Toán 11 Tập 1: Cho hai hàm số y = f(x) = và y = g(x) = ...
Thực hành 3 trang 83 Toán 11 Tập 1: Xét tính liên tục của hàm số ...
Thực hành 4 trang 83 Toán 11 Tập 1: Cho hàm số f(x) = 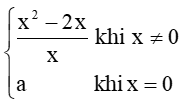
Thực hành 5 trang 84 Toán 11 Tập 1: Xét tính liên tục của hàm số: a) y = + 3 - x;...
Bài 1 trang 84 Toán 11 Tập 1: Xét tính liên tục của hàm số sau:
Bài 2 trang 84 Toán 11 Tập 1: Cho hàm số f(x) = 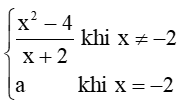
Bài 3 trang 85 Toán 11 Tập 1: Xét tính liên tục của hàm số sau: a) f(x) = ;...
Xem thêm lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Điểm, đường thẳng và mặt phẳng trong không gian
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Chân trời sáng tạo (hay nhất)
- Văn mẫu lớp 11 - Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn 11 – Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn lớp 11 - Chân trời sáng tạo
- Giải SBT Ngữ văn 11 – Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Ngữ văn 11 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Chân trời sáng tạo
- Soạn văn 11 Chân trời sáng tạo (ngắn nhất)
- Giải sgk Tiếng Anh 11 – Friends Global
- Giải sbt Tiếng Anh 11 - Friends Global
- Trọn bộ Từ vựng Tiếng Anh 11 Friends Global đầy đủ nhất
- Bài tập Tiếng Anh 11 Friends Global theo Unit có đáp án
- Giải sgk Vật lí 11 – Chân trời sáng tạo
- Lý thuyết Vật lí 11 – Chân trời sáng tạo
- Giải sbt Vật lí 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Vật lí 11 – Chân trời sáng tạo
- Giải sgk Hóa học 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Hóa học 11 – Chân trời sáng tạo
- Lý thuyết Hóa 11 - Chân trời sáng tạo
- Giải sbt Hóa học 11 – Chân trời sáng tạo
- Giải sgk Sinh học 11 – Chân trời sáng tạo
- Lý thuyết Sinh học 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Sinh học 11 – Chân trời sáng tạo
- Giải sbt Sinh học 11 – Chân trời sáng tạo
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Chân trời sáng tạo
- Lý thuyết Kinh tế pháp luật 11 – Chân trời sáng tạo
- Giải sbt Kinh tế pháp luật 11 – Chân trời sáng tạo
- Giải sgk Lịch sử 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Lịch sử 11 – Chân trời sáng tạo
- Lý thuyết Lịch sử 11 - Chân trời sáng tạo
- Giải sbt Lịch sử 11 – Chân trời sáng tạo
- Giải sgk Địa lí 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Địa lí 11 – Chân trời sáng tạo
- Lý thuyết Địa lí 11 - Chân trời sáng tạo
- Giải sbt Địa lí 11 – Chân trời sáng tạo
- Giải sgk Hoạt động trải nghiệm 11 – Chân trời sáng tạo

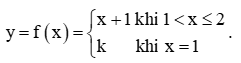
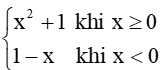 tại điểm x = 0...
tại điểm x = 0...