Vận dụng 2 trang 83 Toán 11 Tập 1 | Chân trời sáng tạo Giải Toán lớp 11
Lời giải Vận dụng 2 trang 83 Toán 11 Tập 1 sách Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11.
Giải Toán 11 Bài 3: Hàm số liên tục
Vận dụng 2 trang 83 Toán 11 Tập 1: Một hãng taxi đưa ra giá cước T(x) (đồng) khi đi quãng đường x (km) cho loại xe 4 chỗ như sau:
T(x) =
Xét tính liên tục của hàm số T(x).
Lời giải:
+) Với x0 ∈ (0; 0,7) hàm số f(x) = 10 000 là hàm đa thức nên liên tục trên (0; 0,7).
+) Với x0 ∈ (0,7; 20) hàm số f(x) = 10 000 + (x – 0,7).14 000 là hàm đa thức nên liên tục trên (0,7; 20).
+) Với x0 ∈ (20; +∞) hàm số f(x) = 280 200 + (x – 20).12 000 là hàm đa thức nên liên tục trên (20; +∞).
+) Tại x0 = 0,7 ta có:
;
[10 000 + (x-0,7).14 000] = 10 000.
Suy ra . Do đó tồn tại .
Mà f(0,7) = 10 000 nên = f(0,7) = 10000.
Vì vậy hàm số liên tục tại x0 = 0,7.
+) Tại x0 = 20 ta có:
[10 000 + (x-0,7).14 000] = 280 200.
[280 200+(x-20).12 000] = 280 200.
Suy ra . Do đó tồn tại .
Mà f(20) = 280 200 nên .
Vì vậy hàm số liên tục tại x = 20.
Vậy hàm số T(x) liên tục trên ℝ.
Xem thêm lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Hoạt động khám phá 1 trang 80 Toán 11 Tập 1: Cho hàm số 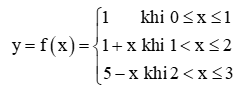
Thực hành 1 trang 81 Toán 11 Tập 1: Xét tính liên tục của hàm số: a) f(x) = 1 – x2 tại điểm x0 = 3;...
Hoạt động khám phá 2 trang 81 Toán 11 Tập 1: Cho hàm số
Thực hành 2 trang 82 Toán 11 Tập 1: Xét tính liên tục của hàm số: trên [1; 2]...
Hoạt động khám phá 3 trang 82 Toán 11 Tập 1: Cho hai hàm số y = f(x) = và y = g(x) = ...
Thực hành 3 trang 83 Toán 11 Tập 1: Xét tính liên tục của hàm số ...
Thực hành 4 trang 83 Toán 11 Tập 1: Cho hàm số f(x) = 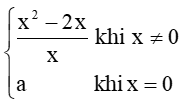
Thực hành 5 trang 84 Toán 11 Tập 1: Xét tính liên tục của hàm số: a) y = + 3 - x;...
Bài 1 trang 84 Toán 11 Tập 1: Xét tính liên tục của hàm số sau:
Bài 2 trang 84 Toán 11 Tập 1: Cho hàm số f(x) = 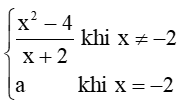
Bài 3 trang 85 Toán 11 Tập 1: Xét tính liên tục của hàm số sau: a) f(x) = ;...
Xem thêm lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Điểm, đường thẳng và mặt phẳng trong không gian
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Chân trời sáng tạo (hay nhất)
- Văn mẫu lớp 11 - Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn 11 – Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn lớp 11 - Chân trời sáng tạo
- Giải SBT Ngữ văn 11 – Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Ngữ văn 11 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Chân trời sáng tạo
- Soạn văn 11 Chân trời sáng tạo (ngắn nhất)
- Giải sgk Tiếng Anh 11 – Friends Global
- Giải sbt Tiếng Anh 11 - Friends Global
- Trọn bộ Từ vựng Tiếng Anh 11 Friends Global đầy đủ nhất
- Bài tập Tiếng Anh 11 Friends Global theo Unit có đáp án
- Giải sgk Vật lí 11 – Chân trời sáng tạo
- Lý thuyết Vật lí 11 – Chân trời sáng tạo
- Giải sbt Vật lí 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Vật lí 11 – Chân trời sáng tạo
- Giải sgk Hóa học 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Hóa học 11 – Chân trời sáng tạo
- Lý thuyết Hóa 11 - Chân trời sáng tạo
- Giải sbt Hóa học 11 – Chân trời sáng tạo
- Giải sgk Sinh học 11 – Chân trời sáng tạo
- Lý thuyết Sinh học 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Sinh học 11 – Chân trời sáng tạo
- Giải sbt Sinh học 11 – Chân trời sáng tạo
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Chân trời sáng tạo
- Lý thuyết Kinh tế pháp luật 11 – Chân trời sáng tạo
- Giải sbt Kinh tế pháp luật 11 – Chân trời sáng tạo
- Giải sgk Lịch sử 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Lịch sử 11 – Chân trời sáng tạo
- Lý thuyết Lịch sử 11 - Chân trời sáng tạo
- Giải sbt Lịch sử 11 – Chân trời sáng tạo
- Giải sgk Địa lí 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Địa lí 11 – Chân trời sáng tạo
- Lý thuyết Địa lí 11 - Chân trời sáng tạo
- Giải sbt Địa lí 11 – Chân trời sáng tạo
- Giải sgk Hoạt động trải nghiệm 11 – Chân trời sáng tạo



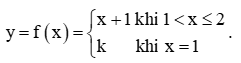
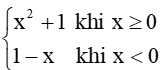 tại điểm x = 0...
tại điểm x = 0...