Toán 11 Bài 1 (Chân trời sáng tạo): Đạo hàm

Giải Toán 11 Bài 1: Đạo hàm

Giải Toán 11 trang 36 Tập 2

Hoạt động khởi động trang 36 Toán 11 Tập 2: Đạo hàm là một khái niệm quan trọng của Giải tích. Đạo hàm cho biết “tốc độ thay đổi” của hàm số theo biến số. Trong chương này, chúng ta sẽ tìm hiểu về đạo hàm, ý nghĩa hình học của đạo hàm, các quy tắc tính đạo hàm. Chúng ta cũng tìm hiểu về đạo hàm cấp hai và giải quyết một số vấn đề thực tiễn gắn với đạo hàm.

Một vật được thả từ trực thăng. Làm thế nào để biết được vận tốc rơi của vật tại một thời điểm bất kì?

Lời giải:

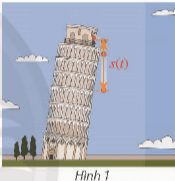
Để biết được vận tốc rơi của vật tại một thời điểm bất kì thì ta xác định hàm số biểu diễn độ cao của vật đó khi được thả từ chiếc trực thăng. Sau đó ta tính đạo hàm hàm số vừa tìm được.

Giải Toán 11 trang 37 Tập 2

Hoạt động khởi động trang 37 Toán 11 Tập 2: Giữa tốc độ của xe và quãng đường mà xe đi được có mối liên hệ như thế nào? Nếu biết quãng đường s(t) tại mọi điểm t thì có thể tính được tốc độ của xe tại mỗi thời điểm không?

Lời giải:

Sau khi học xong bài này, ta giải quyết được:

Tốc độ của xe cho biết tốc độ thay đổi của quãng đường của xe đi được theo thời gian. Nếu biết quãng đường tại mọi thời điểm thì có thể tính được tốc độ của xe tại mọi thời điểm (dựa vào phép tính đạo hàm).

1. Đạo hàm

Hoạt động khám phá 1 trang 37 Toán 11 Tập 2: Quãng đường rơi tự do của một vật được biểu diễn bởi công thức s(t) = 4,9t² với t là thời gian tính bằng giây và s tính bằng mét.

Vận tốc trung bình của chuyển động này trên khoảng thời gian [5; t] hoặc [t; 5] được tính bằng công thức $\frac{s\left(t\right)-s\left(5\right)}{t-5}$.

a) Hoàn thiện bảng sau về vận tốc trung bình trong những khoảng thời gian khác nhau. Nêu nhận xét về $\frac{s\left(t\right)-s\left(5\right)}{t-5}$ khi t càng gần 5.

b) Giới hạn $\underset{t\to 5}{\lim }\frac{s\left(t\right)-s\left(5\right)}{t-5}$được gọi là vận tốc tức thời của chuyển động tại thời điểm t₀ = 5. Tính giá trị này.

c) Tính giới hạn $\underset{t\to t_0}{\lim }\frac{s\left(t\right)-s\left(t_0\right)}{t-t_0}$ để xác định vận tốc tức thời của chuyển động tại thời điềm t₀ nào đó trong quá trình rơi của vật.

Lời giải:

a) • Với t ∈ [5; 5,1], chọn t = 5,1 ta có:

$\frac{s\left(t\right)-s\left(5\right)}{t-5}=\frac{4,9.5,1^2-4,9.5^2}{5,1-5}=49,49.$

• Với t ∈ [5; 5,05], chọn t = 5,05 ta có:

$\frac{s\left(t\right)-s\left(5\right)}{t-5}=\frac{4,9.5,{05}^2-4,9.5^2}{5,05-5}=49,245$.

• Với t ∈ [5; 5,01], chọn t = 5,01 ta có:

$\frac{s\left(t\right)-s\left(5\right)}{t-5}=\frac{4,9.5,{01}^2-4,9.5^2}{5,01-5}=49,049$.

• Với t ∈ [5; 5,001], chọn t = 5,001 ta có:

$\frac{s\left(t\right)-s\left(5\right)}{t-5}=\frac{4,9.5,{001}^2-4,9.5^2}{5,001-5}=49,0049$.

• Với t ∈ [4,999; 5], chọn t = 4,999 ta có:

$\frac{s\left(t\right)-s\left(5\right)}{t-5}=\frac{4,9.4,{999}^2-4,9.5^2}{4,999-5}=49,9951$.

• Với t ∈ [4,99; 5], chọn t = 4,99 ta có:

$\frac{s\left(t\right)-s\left(5\right)}{t-5}=\frac{4,9.4,{99}^2-4,9.5^2}{4,99-5}=49,951$.

Từ đó ta có bảng sau:

Ta thấy $\frac{s\left(t\right)-s\left(5\right)}{t-5}$càng gần 49 khi t càng gần 5.

b) $\underset{t\to 5}{\lim }\frac{s\left(t\right)-s\left(5\right)}{t-5}=\underset{t\to 5}{\lim }\frac{4,9t^2-4,9.5^2}{t-5}$

$=\underset{t\to 5}{\lim }\frac{4,9\left(t^2-5^2\right)}{t-5}=\underset{t\to 5}{\lim }\frac{4,9\left(t-5\right)\left(t+5\right)}{t-5}$

$=\underset{t\to 5}{\lim }4,9\left(t+5\right)=4,9\left(5+5\right)=49.$

c) $\underset{t\to t_0}{\lim }\frac{s\left(t\right)-s\left(t_0\right)}{t-t_0}=\underset{t\to t_0}{\lim }\frac{4,9t^2-4,9t_0^2}{t-t_0}$

$=\underset{t\to t_0}{\lim }\frac{4,9\left(t^2-t_0^2\right)}{t-t_0}=\underset{t\to t_0}{\lim }\frac{4,9\left(t-t_0\right)\left(t+t_0\right)}{t-t_0}$

$=\underset{t\to t_0}{\lim }4,9\left(t+t_0\right)=4,9\left(t_0+t_0\right)=9,8t_0.$

Giải Toán 11 trang 39 Tập 2

Thực hành 1 trang 39 Toán 11 Tập 2: Tính đạo hàm của hàm số f(x) = x³.

Lời giải:

Với bất kì x₀ ∈ ℝ, ta có:

$f^{\text{'}}\left(x_0\right)=\underset{x\to x_0}{\lim }\frac{x^3-x_0^3}{x-x_0}=\underset{x\to x_0}{\lim }\frac{\left(x-x_0\right)\left(x^2+x.x_0+x_0^2\right)}{x-x_0}$

$=\underset{x\to x_0}{\lim }\left(x^2+x.x_0+x_0^2\right)=x_0^2+x_0.x_0+x_0^2=3x_0^2$.

Vậy $f^{\text{'}}\left(x\right)={\left(x^3\right)}^{\text{'}}=3x^2$ trên ℝ.

Vận dụng trang 39 Toán 11 Tập 2: Với tình huống trong Hoạt động khám phá 1, hãy tính vận tốc tức thời của chuyển động lúc t = 2.

Lời giải:

Với bất kì t₀ ∈ ℝ, ta có:

$s^{\text{'}}\left(t_0\right)=\underset{t\to t_0}{\lim }\frac{s\left(t\right)-s\left(t_0\right)}{t-t_0}=9,8t_0$.

Do đó $s^{\text{'}}\left(t\right)=9,8t$ trên ℝ.

Vậy vận tốc tức thời của chuyển động lúc t = 2 là:

$v\left(2\right)=s^{\text{'}}\left(2\right)=9,8.2=19,6$ (m/s).

2. Ý nghĩa hình học của đạo hàm

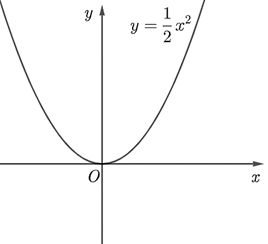
Hoạt động khám phá 2 trang 39 Toán 11 Tập 2: Cho hàm số $y=f\left(x\right)=\frac{1}{2}{x}^2$có đồ thị (C) và điểm $M\left(1;\frac{1}{2}\right)$thuộc (C).

a) Vẽ (C) và tính f' (1).

b) Vẽ đường thẳng d đi qua điểm M và có hệ số góc bằng f' (1). Nêu nhận xét về vị trí tương đối giữa d và (C).

Lời giải:

a) Đồ thị hàm số $\left(C\right):y=\frac{1}{2}{x}^2$ được vẽ như hình bên dưới.

Ta có $f^{\text{'}}\left(1\right)=\underset{t\to 1}{\lim }\frac{f\left(x\right)-f\left(1\right)}{x-1}=\underset{t\to 1}{\lim }\frac{\frac{1}{2}{x}^2-\frac{1}{2}}{x-1}$

$=\underset{t\to 1}{\lim }\frac{\frac{1}{2}\left(x^2-1\right)}{x-1}=\underset{t\to 1}{\lim }\frac{\frac{1}{2}\left(x-1\right)\left(x+1\right)}{x-1}$

$=\underset{t\to 1}{\lim }\frac{1}{2}\left(x+1\right)=\frac{1}{2}\left(x+1\right)=1$.

b) Theo đề bài, đường thẳng d đi qua $M\left(1;\frac{1}{2}\right)$ và có hệ số góc bằng k = f' (1) = 1 nên:

$y-\frac{1}{2}=1\left(x-1\right)\iff y-\frac{1}{2}=x-1\iff y=x-\frac{1}{2}$.

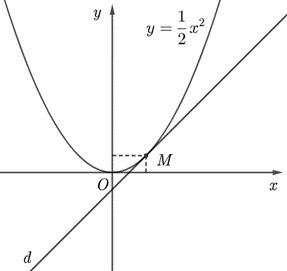
Lấy điểm $M\left(1;\frac{1}{2}\right)$, vẽ đường thẳng $\left(d\right):y=x-\frac{1}{2}$, ta có hình vẽ:

Nhận xét: Đường thẳng d cắt đồ thị hàm số (C) tại duy nhất tại điểm $M\left(1;\frac{1}{2}\right)$.

Khi đó, đường thẳng d tiếp xúc với đồ thị hàm số (C) tại điểm $M\left(1;\frac{1}{2}\right)$.

Giải Toán 11 trang 40 Tập 2

Thực hành 2 trang 40 Toán 11 Tập 2: Cho (C) là đồ thị của hàm số $f\left(x\right)=\frac{1}{x}$ và điểm M(1; 1) ∈ (C). Tính hệ số góc của tiếp tuyến của (C) tại điểm M và viết phương trình tiếp tuyến đó.

Lời giải:

Ta có ${\left(\frac{1}{x}\right)}^{\text{'}}=-\frac{1}{x^2}$ nên tiếp tuyến của (C) tại điểm M có hệ số góc $f^{\text{'}}\left(x\right)=-\frac{1}{1^2}=-1$.

Phương trình tiếp tuyến của (C) tại điểm M là:

y – 1 = (–1)(x – 1) ⇔ y – 1 = 1 – x ⇔ y = – x + 2.

Vậy hệ số góc của tiếp tuyến của (C) tại điểm M bằng –1 và phương trình tiếp tuyến là y = – x + 2.

3. Số e

Hoạt động khám phá 3 trang 40 Toán 11 Tập 2: Một người gửi tiết kiệm khoản tiền A triệu đồng (gọi là vốn) với lãi suất r/năm theo thể thức lãi kép (tiền lãi sau mỗi kì hạn được cộng gộp vào vốn). Tính tổng số tiền vốn và lãi sau một năm của người gửi nếu kì hạn là

a) một năm;

b) một tháng.

Lưu ý: Nếu một năm được chia thành n kì hạn (n ∈ ℕ*) thì lãi suất mỗi kì hạn là $\frac{r}{n}$.

Lời giải:

a) Nếu người gửi với kì hạn một năm.

Số tiền lãi sau một năm là A.r.

Tổng số tiền vốn và lãi sau một năm của người gửi là:

A + Ar = A(1 + r).

b) Nếu người gửi với kì hạn một tháng.

Số tiền lãi sau tháng thứ nhất là: $A.\frac{r}{12}$.

Tổng số tiền vốn và lãi sau tháng thứ nhất là:

$A+A.\frac{r}{12}=A\left(1+\frac{r}{12}\right)$.

Số tiền lãi sau tháng thứ hai là: $A\left(1+\frac{r}{12}\right)\cdot \frac{r}{12}$.

Tổng số tiền vốn và lãi sau tháng thứ hai là:

$$\begin{gathered} A\left(1+\frac{r}{12}\right)+A\left(1+\frac{r}{12}\right)\cdot \frac{r}{12} \\ =A\left(1+\frac{r}{12}\right)\left(1+\frac{r}{12}\right)=A{\left(1+\frac{r}{12}\right)}^2 \end{gathered}$$

Số tiền lãi sau tháng thứ ba là: $A{\left(1+\frac{r}{12}\right)}^2\cdot \frac{r}{12}$.

Tổng số tiền vốn và lãi sau tháng thứ ba là:

$$\begin{gathered} A{\left(1+\frac{r}{12}\right)}^2+A{\left(1+\frac{r}{12}\right)}^2\cdot \frac{r}{12} \\ =A{\left(1+\frac{r}{12}\right)}^2\cdot \left(1+\frac{r}{12}\right)=A{\left(1+\frac{r}{12}\right)}^3 \end{gathered}$$

...

Tương tự, tổng số tiền vốn và lãi sau 1 năm (tức là sau tháng thứ 12) là: $A{\left(1+\frac{r}{12}\right)}^{12}.$

Vậy tổng số tiền vốn và lãi sau một năm là $A{\left(1+\frac{r}{12}\right)}^{12}.$

Giải Toán 11 trang 41 Tập 2

Thực hành 3 trang 41 Toán 11 Tập 2: Một người gửi tiết kiệm khoản tiền 5 triệu đồng vào ngân hàng với lãi suất 4% năm và theo thể thức lãi kép liên tục. Tính tổng số tiền vốn và lãi mà người đó nhận được sau:

a) 1 ngày.

b) 30 ngày.

(Luôn coi một năm có 365 ngày.)

Lời giải:

a) Tổng số tiền vốn và lãi mà người đó nhận được sau 1 ngày là:

$T=5000000.e^{0,04\cdot \frac{1}{365}}\approx 5000548$ (đồng)

Vậy tổng số tiền vốn và lãi mà người đó nhận được sau 1 ngày khoảng 5 000 548 đồng.

b) Tổng số tiền vốn và lãi mà người đó nhận được sau 30 ngày là:

$T=5000000.e^{0,04\cdot \frac{30}{365}}\approx 5016465$ (đồng).

Vậy tổng số tiền vốn và lãi mà người đó nhận được sau 30 ngày khoảng 5 016 465 đồng.

Bài tập

Bài 1 trang 41 Toán 11 Tập 2: Dùng định nghĩa để tính đạo hàm của các hàm số sau:

a) f(x) = −x²;

b) f(x) = x² − 2x;

c) $f\left(x\right)=\frac{4}{x}$.

Lời giải:

a) Với bất kì x₀ ∈ ℝ, ta có:

$f^{\text{'}}\left(x_0\right)=\underset{x\to x_0}{\lim }\frac{\left(-x^2\right)-\left(-x_0^2\right)}{x-x_0}=\underset{x\to x_0}{\lim }\frac{-x^2+x_0^2}{x-x_0}$

$=\underset{x\to x_0}{\lim }\frac{-\left(x-x_0\right)\left(x+x_0\right)}{x-x_0}=\underset{x\to x_0}{\lim }\left(-x-x_0\right)$

$=-x_0-x_0=-2x_0$.

Vậy $f^{\text{'}}\left(x\right)={\left(-x^2\right)}^{\text{'}}=-2x$ trên ℝ.

b) Với bất kì x₀ ∈ ℝ, ta có:

$f^{\text{'}}\left(x_0\right)=\underset{x\to x_0}{\lim }\frac{\left(x^3-2x\right)-\left(x_0^3-2x_0\right)}{x-x_0}$

$=\underset{x\to x_0}{\lim }\frac{x^3-2x-x_0^3+2x_0}{x-x_0}$$=\underset{x\to x_0}{\lim }\frac{\left(x^3-x_0^3\right)-\left(2x-2x_0\right)}{x-x_0}$

$=\underset{x\to x_0}{\lim }\frac{\left(x-x_0\right)\left(x^2+x.x_0+x_0^2\right)-2\left(x-x_0\right)}{x-x_0}$

$=\underset{x\to x_0}{\lim }\frac{\left(x-x_0\right)\left(x^2+x.x_0+x_0^2-2\right)}{x-x_0}$

$=\underset{x\to x_0}{\lim }\left(x^2+x.x_0+x_0^2-2\right)$

$=x_0^2+x_0.x_0+x_0^2-2=3x_0^2-2$.

Vậy $f^{\text{'}}\left(x\right)={\left(x^3-2x\right)}^{\text{'}}=3x^2-2$ trên ℝ.

c) Với bất kì x₀ ≠ 0, ta có:

$f^{\text{'}}\left(x_0\right)=\underset{x\to x_0}{\lim }\frac{\frac{4}{x}-\frac{4}{x_0}}{x-x_0}=\underset{x\to x_0}{\lim }\frac{\frac{4x_0-4x}{x{x}_0}}{x-x_0}$$=\underset{x\to x_0}{\lim }\frac{4x_0-4x}{x{x}_0\left(x-x_0\right)}$

$=\underset{x\to x_0}{\lim }\frac{-4\left(x-x_0\right)}{x{x}_0\left(x-x_0\right)}=\underset{x\to x_0}{\lim }\frac{-4}{x{x}_0}=\frac{-4}{x_0.x_0}=-\frac{4}{x_0^2}$.

Vậy $f^{\text{'}}\left(x\right)={\left(\frac{4}{x}\right)}^{\text{'}}=-\frac{4}{x^2}$ trên các khoảng (−∞; 0) và (0; +∞).

Bài 2 trang 41 Toán 11 Tập 2: Cho hàm số f(x) = −2x² có đồ thị (C) và điểm A(1; −2) ∈ (C). Tính hệ số góc của tiếp tuyến với (C) tại điểm A.

Lời giải:

Hệ số góc của tiếp tuyến với (C) tại điểm A là:

$f^{\text{'}}\left(1\right)=\underset{x\to 1}{\lim }\frac{\left(-2x^2\right)-\left(-2.1^2\right)}{x-1}=\underset{x\to 1}{\lim }\frac{-2x^2+2}{x-1}$

$=\underset{x\to 1}{\lim }\frac{-2\left(x^2-1\right)}{x-1}=\underset{x\to 1}{\lim }\frac{-2\left(x-1\right)\left(x+1\right)}{x-1}$

$=\underset{x\to 1}{\lim }\left(-2\left(x+1\right)\right)=-2\left(1+1\right)=-4$.

Vậy hệ số góc của tiếp tuyến với (C) tại điểm A là −4.

Giải Toán 11 trang 42 Tập 2

Bài 3 trang 42 Toán 11 Tập 2: Viết phương trình tiếp tuyến của đồ thị hàm số y = x³.

a) Tại điểm (−1; 1);

b) Tại điểm có hoành độ bằng 2.

Lời giải:

Ta có: (x³)′=3x².

a) Vì điểm M(−1; 1) không thuộc đồ thị hàm số (C) nên không có phương trình tiếp tuyến tại điểm M(−1; 1).

b) Với x₀=2⇔y₀=2³=8. Do đó N(2;8).

Tiếp tuyến của (C) tại điểm N(2;8) có hệ số góc là:

f′(2)=3.2²=12.

Phương trình tiếp tuyến của (C) tại điểm N là:

y–8=12(x−2)⇔y=12x–24+8⇔y=12x–16.

Bài 4 trang 42 Toán 11 Tập 2: Một chuyển động thẳng xác định bởi phương trình s(t) = 4t³ + 6t + 2, trong đó tính bằng mét và t là thời gian tính bằng giây. Tính vận tốc tức thời của chuyển động tại t = 2.

Lời giải:

Vận tốc tức thời của chuyển động tại t = 2 là:

$v\left(2\right)=s^{\text{'}}\left(2\right)=\underset{t\to 2}{\lim }\frac{s\left(t\right)-s\left(2\right)}{t-2}$

$=\underset{t\to 2}{\lim }\frac{\left(4t^3+6t+2\right)-\left(4.2^3+6.2+2\right)}{t-2}$

$=\underset{t\to 2}{\lim }\frac{4t^3+6t+2-46}{t-2}=\underset{t\to 2}{\lim }\frac{4t^3+6t-44}{t-2}$

$=\underset{t\to 2}{\lim }\frac{2\left(2t^3+3t-22\right)}{t-2}=\underset{t\to 2}{\lim }\frac{2\left(t-2\right)\left(2t^2+4t-11\right)}{t-2}$

$=\underset{t\to 2}{\lim }2\left(2t^2+4t-11\right)=2\left(2.2^2+4.2-11\right)=54$.

Vậy vận tốc tức thời của chuyển động lúc t = 2 là v(2) = 54 m/s.

Bài 5 trang 42 Toán 11 Tập 2: Một người gửi tiết kiệm khoản tiền 10 triệu đồng vào một ngân hàng với lãi suất 5%/năm. Tính tổng số tiền vốn và lãi mà người đó nhận được sau một năm, nếu tiền lãi được tính theo thể thức

a) lãi kép với kì hạn 6 tháng.

b) lãi kép liên tục.

Lời giải:

a) Nếu tiền lãi được tính theo thể thứclãi kép với kì hạn 6 tháng.

Tổng số tiền vốn và lãi người đó nhận được sau 1 năm là:

$T=A.{\left(1+\frac{r}{n}\right)}^n=1000000000.{\left(1+\frac{0,05}{2}\right)}^2=10506250$ (đồng).

Vậy tổng số tiền vốn và lãi người đó nhận được sau 1 năm là 10 506 250 đồng, nếu tiền lãi được tính theo thể thức lãi kép với kì hạn 6 tháng.

b) Nếu tiền lãi được tính theo thể thức lãi kép liên tục.

Tổng số tiền vốn và lãi người đó nhận được sau 1 năm là:

$T=A.e^{rt}=1000000000.e^{0,05}\approx 10512711$ (đồng).

Vậy tổng số tiền vốn và lãi người đó nhận được sau 1 năm là 10 512 711 đồng, nếu tiền lãi được tính theo thể thức lãi kép liên tục.

Bài 6 trang 42 Toán 11 Tập 2: Trên Mặt Trăng, quãng đường rơi tư do của một vật được cho bởi công thức h(t) = 0,81t², với được tính bằng giây và tính bằng mét. Hãy tính vận tốc tức thời của vật được thả rơi tự do trên Mặt Trăng tại thời điểm t = 2.

Lời giải:

(Nguồn: https:/www.britannica.complace/Moon)

Ta có $h^{\text{'}}\left(2\right)=\underset{t\to 2}{\lim }\frac{h\left(t\right)-h\left(2\right)}{t-2}=\underset{t\to 2}{\lim }\frac{0,81t^2-0,81.2^2}{t-2}$

$=\underset{t\to 2}{\lim }\frac{0,81\left(t^2-2^2\right)}{t-2}=\underset{t\to 2}{\lim }\frac{0,81\left(t-2\right)\left(t+2\right)}{t-2}$

$=\underset{t\to 2}{\lim }0,81\left(t+2\right)=0,81\left(2+2\right)=3,24$.

Vậy vận tốc tức thời của chuyển động lúc t = 2 là v(2) = h' (2) = 3,24 m/s.

Lý thuyết Đạo hàm

1. Đạo hàm

Cho hàm số y = f(x) xác định trên khoảng $\left(a;b\right)$ và điểm $x_0\in \left(a;b\right)$.

Nếu tồn tại giới hạn (hữu hạn)

$\underset{x\to x_0}{lim}\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}$

thì giới hạn đó được gọi là đạo hàm của f(x) tại điểm $x_0$, kí hiệu là $f^{\prime }\left(x_0\right)$ hoặc $y^{\prime }\left(x_0\right)$.

Vậy:

$f^{\prime }\left(x_0\right)=\underset{x\to x_0}{lim}\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}$.

Chú ý:

- Cho hàm số y = f(x) xác định trên khoảng (a; b). Nếu hàm số này có đạo hàm tại mọi điểm $x\in \left(a;b\right)$ thì ta nói nó có đạo hàm trên khoảng (a; b), kí hiệu y’ hoặc f’(x).

- Cho hàm số y = f(x) xác định trên khoảng (a; b), có đạo hàm tại $x_0\in \left(a;b\right)$.

a) Đại lượng $\mathrm{\Delta }x=x-x_0$ gọi là số gia của biến tại $x_0$. Đại lượng $y=f\left(x\right)-f\left(x_0\right)$ gọi là số gia tương ứng của hàm số. Khi đó, $x=x_0+\mathrm{\Delta }x$ và

$f^{\prime }\left(x_0\right)=\underset{\mathrm{\Delta }x\to 0}{lim}\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}=\underset{\mathrm{\Delta }x\to 0}{lim}\frac{f\left(x_0+\mathrm{\Delta }x\right)-f\left(x_0\right)}{\mathrm{\Delta }x}$.

b) Tỉ số $\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}$ biểu thị tốc độ thay đổi trung bình của đại lượng y theo đại lượng x trong khoảng từ $x_0$ đến $x_0+\mathrm{\Delta }x$; còn $f^{\prime }\left(x_0\right)$ biểu thị tốc độ thay đổi (tức thời) của đại lượng y theo đại lượng x tại điểm $x_0$.

2. Ý nghĩa vật lí của đạo hàm

- Nếu hàm số s = f(t) biểu thị quãng đường di chuyển của vật theo thời gian t thì $f^{\prime }\left(t_0\right)$ biểu thị tốc độ tức thời của chuyển động tại thời điểm $t_0$.

- Nếu hàm số T = f(t) biểu thị nhiệt độ T theo thời gian t thì $f^{\prime }\left(t_0\right)$ biểu thị tốc độ thay đổi nhiệt độ theo thời gian tại thời điểm $t_0$.

3. Ý nghĩa hình học của đạo hàm

Đạo hàm của hàm số $y=f\left(x\right)$ tại điểm $x_0$ là hệ số góc của tiếp tuyến $M_{0}T$ với đồ thị (C) của hàm số tại điểm $M_0\left(x_0;f\left(x_0\right)\right)$.

Tiếp tuyến $M_{0}T$ có phương trình là $y-f\left(x_0\right)=f^{\prime }\left(x_0\right)\left(x-x_0\right)$.

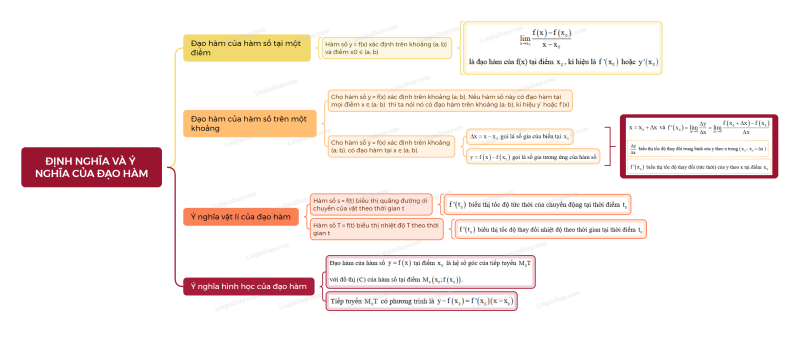
Sơ đồ tư duy Đạo hàm

a

Xem thêm Lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 3: Hàm số mũ. Hàm số lôgarit

Bài 4: Phương trình, bất phương trình mũ và lôgarit

Bài tập cuối chương 6 trang 34

Bài 2: Các quy tắc tính đạo hàm

Bài tập cuối chương 7 trang 51