Giải Toán 11 trang 39 Tập 2 Chân trời sáng tạo

Với giải bài tập Toán 11 trang 39 Tập 2 trong Bài 1: Đạo hàm sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 11 trang 39 Tập 2.

1 290 28/11/2023

Trang trước

Trang sau

Giải Toán 11 trang 39 Tập 2

Thực hành 1 trang 39 Toán 11 Tập 2: Tính đạo hàm của hàm số f(x) = x³.

Lời giải:

Với bất kì x₀ ∈ ℝ, ta có:

$f^{'} (x_{0}) = \lim_{x \to x_{0}} \frac{x^{3} - x_{0}^{3}}{x - x_{0}} = \lim_{x \to x_{0}} \frac{(x - x_{0}) (x^{2} + x . x_{0} + x_{0}^{2})}{x - x_{0}}$

$= \lim_{x \to x_{0}} (x^{2} + x . x_{0} + x_{0}^{2}) = x_{0}^{2} + x_{0} . x_{0} + x_{0}^{2} = 3 x_{0}^{2}$ .

Vậy $f^{'} (x) = {(x^{3})}^{'} = 3 x^{2}$ trên ℝ.

Vận dụng trang 39 Toán 11 Tập 2: Với tình huống trong Hoạt động khám phá 1, hãy tính vận tốc tức thời của chuyển động lúc t = 2.

Lời giải:

Với bất kì t₀ ∈ ℝ, ta có:

$s^{'} (t_{0}) = \lim_{t \to t_{0}} \frac{s (t) - s (t_{0})}{t - t_{0}} = 9, 8 t_{0}$ .

Do đó $s^{'} (t) = 9, 8 t$ trên ℝ.

Vậy vận tốc tức thời của chuyển động lúc t = 2 là:

$v (2) = s^{'} (2) = 9, 8 . 2 = 19, 6$ (m/s).

2. Ý nghĩa hình học của đạo hàm

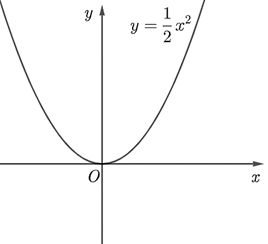
Hoạt động khám phá 2 trang 39 Toán 11 Tập 2: Cho hàm số $y = f (x) = \frac{1}{2} x^{2}$ có đồ thị (C) và điểm $M (1; \frac{1}{2})$ thuộc (C).

a) Vẽ (C) và tính f' (1).

b) Vẽ đường thẳng d đi qua điểm M và có hệ số góc bằng f' (1). Nêu nhận xét về vị trí tương đối giữa d và (C).

Lời giải:

a) Đồ thị hàm số $(C) : y = \frac{1}{2} x^{2}$ được vẽ như hình bên dưới.

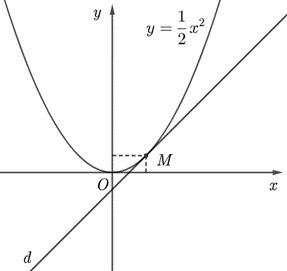
Hoạt động khám phá 2 trang 39 Toán 11 Tập 2

Ta có $f^{'} (1) = \lim_{t \to 1} \frac{f (x) - f (1)}{x - 1} = \lim_{t \to 1} \frac{\frac{1}{2} x^{2} - \frac{1}{2}}{x - 1}$

$= \lim_{t \to 1} \frac{\frac{1}{2} (x^{2} - 1)}{x - 1} = \lim_{t \to 1} \frac{\frac{1}{2} (x - 1) (x + 1)}{x - 1}$

$= \lim_{t \to 1} \frac{1}{2} (x + 1) = \frac{1}{2} (x + 1) = 1$ .

b) Theo đề bài, đường thẳng d đi qua $M (1; \frac{1}{2})$ và có hệ số góc bằng k = f' (1) = 1 nên:

$y - \frac{1}{2} = 1 (x - 1) \Leftrightarrow y - \frac{1}{2} = x - 1 \Leftrightarrow y = x - \frac{1}{2}$ .

Lấy điểm $M (1; \frac{1}{2})$ , vẽ đường thẳng $(d) : y = x - \frac{1}{2}$ , ta có hình vẽ:

Hoạt động khám phá 2 trang 39 Toán 11 Tập 2

Nhận xét: Đường thẳng d cắt đồ thị hàm số (C) tại duy nhất tại điểm $M (1; \frac{1}{2})$ .

Khi đó, đường thẳng d tiếp xúc với đồ thị hàm số (C) tại điểm $M (1; \frac{1}{2})$ .

Xem thêm Lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Giải Toán 11 trang 36 Tập 2

Giải Toán 11 trang 37 Tập 2

Giải Toán 11 trang 39 Tập 2

Giải Toán 11 trang 40 Tập 2

Giải Toán 11 trang 41 Tập 2

Giải Toán 11 trang 42 Tập 2

Xem thêm Lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Hoạt động khởi động trang 36 Toán 11 Tập 2: Đạo hàm là một khái niệm quan trọng của Giải tích. Đạo hàm cho biết “tốc độ thay đổi” của hàm số theo biến số...

Hoạt động khởi động trang 37 Toán 11 Tập 2: Giữa tốc độ của xe và quãng đường mà xe đi được có mối liên hệ như thế nào...

Hoạt động khám phá 1 trang 37 Toán 11 Tập 2: Quãng đường rơi tự do của một vật được biểu diễn bởi công thức s(t) = 4,9t² với t là thời gian tính bằng giây và s tính bằng mét...

Thực hành 1 trang 39 Toán 11 Tập 2: Tính đạo hàm của hàm số f(x) = x³...

Vận dụng trang 39 Toán 11 Tập 2: Với tình huống trong Hoạt động khám phá 1, hãy tính vận tốc tức thời của chuyển động lúc t = 2...

Hoạt động khám phá 2 trang 39 Toán 11 Tập 2: Cho hàm số $y = f (x) = \frac{1}{2} x^{2}$ có đồ thị (C) và điểm $M (1; \frac{1}{2})$ thuộc (C)...

Thực hành 2 trang 40 Toán 11 Tập 2: Cho (C) là đồ thị của hàm số $f (x) = \frac{1}{x}$ và điểm M(1; 1) ∈ (C). Tính hệ số góc của tiếp tuyến của (C) tại điểm M và viết phương trình tiếp tuyến đó...

Hoạt động khám phá 3 trang 40 Toán 11 Tập 2: Một người gửi tiết kiệm khoản tiền A triệu đồng (gọi là vốn) với lãi suất r/năm theo thể thức lãi kép...

Thực hành 3 trang 41 Toán 11 Tập 2: Một người gửi tiết kiệm khoản tiền 5 triệu đồng vào ngân hàng với lãi suất 4% năm và theo thể thức lãi kép liên tục...

Bài 1 trang 41 Toán 11 Tập 2: Dùng định nghĩa để tính đạo hàm của các hàm số sau: a) f(x) = −x²; b) f(x) = x²− 2x; c) $f (x) = \frac{4}{x}$ ...

Bài 2 trang 41 Toán 11 Tập 2: Cho hàm số f(x) = −2x² có đồ thị (C) và điểm A(1; −2) ∈ (C). Tính hệ số góc của tiếp tuyến với (C) tại điểm A...

Bài 3 trang 42 Toán 11 Tập 2: Viết phương trình tiếp tuyến của đồ thị hàm số y = x³. a) Tại điểm (−1; 1); b) Tại điểm có hoành độ bằng 2...

Bài 4 trang 42 Toán 11 Tập 2: Một chuyển động thẳng xác định bởi phương trình s(t) = 4t³ + 6t + 2, trong đó tính bằng mét và t là thời gian tính bằng giây...

Bài 5 trang 42 Toán 11 Tập 2: Một người gửi tiết kiệm khoản tiền 10 triệu đồng vào một ngân hàng với lãi suất 5%/năm. Tính tổng số tiền vốn và lãi mà người đó nhận được sau một năm...

Bài 6 trang 42 Toán 11 Tập 2: Trên Mặt Trăng, quãng đường rơi tư do của một vật được cho bởi công thức h(t) = 0,81t², với được tính bằng giây và tính bằng mét...

Xem thêm Lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 3: Hàm số mũ. Hàm số lôgarit

Bài 4: Phương trình, bất phương trình mũ và lôgarit

Bài tập cuối chương 6 trang 34

Bài 2: Các quy tắc tính đạo hàm

Bài tập cuối chương 7 trang 51

1 290 28/11/2023

Trang trước

Trang sau

Xem thêm các chương trình khác: