Toán 11 Bài 1 (Chân trời sáng tạo): Giới hạn của dãy số

Giải Toán 11 Bài 1: Giới hạn của dãy số

Bài giảng Toán 11 Bài 1: Giới hạn của dãy số

Giải Toán 11 trang 64 Tập 1

Hoạt động khởi động trang 64 Toán 11 Tập 1:

Bạn nam thứ 1: Số thập phân vô hạn tuần hoàn 0,666... và số $\frac{2}{3}$ là hai số bằng nhau.

Bạn nam thứ 2: Không thể như vậy được, vì 0,6 < $\frac{2}{3}$; 0,66 < $\frac{2}{3}$; 0,666 < $\frac{2}{3}$; ...

Bạn nữ: ???

Lời giải:

Nội dung đang được cập nhật...

1. Giới hạn hữu hạn của dãy số

Hoạt động khám phá 1 trang 64 Toán 11 Tập 1: Cho dãy số (u_n) với $u_n=\frac{{\left(-1\right)}^n}{n}$.

a) Tìm các giá trị còn thiếu trong bảng sau:

b) Với n như thế nào thì |u_n| bé hơn 0,01; 0,001?

c) Một số số hạng của dãy số được biểu diễn trên trục số như Hình 1.

Từ các kết quả trên, có nhận xét gì về khoảng cách từ điểm u_n đến điểm 0 khi n trở lên rất lớn?

Lời giải:

a) Ta có:

Với n = 100 có |u₁₀₀| = 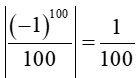= 0,01.

Với n = 1 000 có |u₁₀₀₀| = 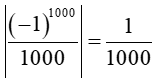= 0,001.

Khi đó ta có bảng:

b) Với n > 100 thì |u_n| < 0,01.

Với n > 1000 thì |u_n| < 0,001.

c) Khi n trở nên rất lớn thì khoảng cách từ điểm u_n đến điểm 0 càng nhỏ.

Giải Toán 11 trang 65 Tập 1

Thực hành 1 trang 65 Toán 11 Tập 1: Tìm các giới hạn sau:

a) $\lim \frac{1}{n^2}$;

b) $\lim {\left(-\frac{3}{4}\right)}^n$.

Lời giải:

a) Ta có: k = 2 là số nguyên dương nên $\lim \frac{1}{n^2}=0$.

b) Ta có: $q=-\frac{3}{4}$ thỏa mãn |q| = 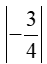= $\frac{3}{4}$ < 1 nên $\lim {\left(-\frac{3}{4}\right)}^n=0$.

Hoạt động khám phá 2 trang 65 Toán 11 Tập 1: Cho dãy số (u_n) với $u_n=\frac{2n+1}{n}$.

a) Cho dãy số (v_n) với v_n = u_n – 2. Tìm giới hạn lim v_n.

b) Biểu diễn các điểm u₁, u₂, u₃, u₄ trên trục số. Có nhận xét gì về vị trí của các điểm u_n khi n trở nên rất lớn?

Lời giải:

a) Ta có: $v_n=\frac{2n+1}{n}-2=\frac{1}{n}$

Khi đó $\lim \frac{1}{n}=0$.

Vậy $\lim v_n=0$.

b) Ta có:$u_1=\frac{2.1+1}{1}=3;u_2=\frac{2.2+1}{2}=\frac{5}{2};u_3=\frac{2.3+1}{3}=\frac{7}{3};u_4=\frac{2.4+1}{4}=\frac{9}{4}$;

Biểu diễn trên trục số, ta được:

Nhận xét: Khi n trở nên rất lớn lớn thì các giá trị u_n càng gần 2.

Thực hành 2 trang 65 Toán 11 Tập 1: Tìm các giới hạn sau:

a) $\lim \left(2+{\left(\frac{2}{3}\right)}^n\right)$;

b)$\lim \left(\frac{1-4n}{n}\right)$.

Lời giải:

a) Đặt $u_n=2+{\left(\frac{2}{3}\right)}^n\iff u_n-2={\left(\frac{2}{3}\right)}^n$

Suy ra $\lim \left(u_n-2\right)=\lim {\left(\frac{2}{3}\right)}^n$

Vì <1 nên $\lim \left(u_n-2\right)=\lim {\left(\frac{2}{3}\right)}^n=0$.

Vậy $\lim \left(2+{\left(\frac{2}{3}\right)}^n\right)=2$.

b) Đặt $u_n=\frac{1-4n}{n}=\frac{1}{n}-4\iff u_n+4=\frac{1}{n}$

Suy ra $\lim \left(u_n+4\right)=\lim \left(\frac{1}{n}\right)=0$.

Vậy $\lim \left(\frac{1-4n}{n}\right)=-4$.

2. Các phép toán về giới hạn hữu hạn của dãy số

Giải Toán 11 trang 66 Tập 1

Hoạt động khám phá 3 trang 66 Toán 11 Tập 1: Ở trên ta đã biết $\lim \left(3+\frac{1}{n^2}\right)=\lim \frac{3n^2+1}{n^2}=1$.

a) Tìm các giới hạn lim 3 và $\lim \frac{1}{n^2}$.

b) Từ đó, nêu nhận xét về $\lim \left(3+\frac{1}{n^2}\right)$ và lim 3 + $\lim \frac{1}{n^2}$.

Lời giải:

a) Ta có: lim 3 = 3, $\lim \frac{1}{n^2}=0$.

b) Đặt $u_n=3+\frac{1}{n^2}\iff u_n-3=\frac{1}{n^2}$

Suy ra $\lim \left(u_n-3\right)=\lim \frac{1}{n^2}=0$

$\Rightarrow \lim u_n=3$

Ta có: lim 3 + $\lim \frac{1}{n^2}$ = 3 + 0 = 3.

Vậy $\lim \left(3+\frac{1}{n^2}\right)$ = lim 3 + $\lim \frac{1}{n^2}$.

Thực hành 3 trang 66 Toán 11 Tập 1: Tìm các giới hạn sau:

a) $\lim \frac{2n^2+3n}{n^2+1}$;

b) $\lim \frac{\sqrt{4n^2+3}}{n}$.

Lời giải:

a) $\lim \frac{2n^2+3n}{n^2+1}=\lim \frac{2+\frac{3}{n}}{1+\frac{1}{n^2}}=2$.

b) Ta có: $\frac{\sqrt{4n^2+3}}{n}=\sqrt{4+\frac{3}{n^2}}$

$\lim \frac{\sqrt{4n^2+3}}{n}=\lim \sqrt{4+\frac{3}{n^2}}=\sqrt{\lim \left(4+\frac{3}{n^2}\right)}=\sqrt{\lim 4+\lim \frac{3}{n^2}}=2$.

3. Tổng của cấp số nhân lùi vô hạn

Giải Toán 11 trang 67 Tập 1

Hoạt động khám phá 4 trang 67 Toán 11 Tập 1: Từ một hình vuông có cạnh bằng 1, tô màu một nửa hình vuông, rồi tô màu một nửa hình còn lại, và cứ tiếp tục như vậy (xem Hình 2).

a) Xác định diện tích u_k của phần hình được tô màu lần thứ k (k = 1, 2, 3, ...).

b) Tính tổng diện tích S_n của phần hình được tô màu sau lần tô thứ n (n = 1, 2, 3, ...).

c) Tìm giới hạn limS_n và so sánh giới hạn này với diện tích hình vuông ban đầu.

Lời giải:

a) Xác định diện tích u_k của phần hình được tô màu lần thứ k (k = 1, 2, 3, ...).

Ta có: u₁ = 1.$\frac{1}{2}=\frac{1}{2}$; u₂ = $\frac{1}{2}.\frac{1}{2}={\left(\frac{1}{2}\right)}^2$; u₃ = $\frac{1}{2}.\frac{1}{2}.\frac{1}{2}={\left(\frac{1}{2}\right)}^3$; u₄ = $\frac{1}{2}.\frac{1}{2}.\frac{1}{2}.\frac{1}{2}={\left(\frac{1}{2}\right)}^4$; ...

Diện tích u_k của phần hình được tô màu lần thứ k là một cấp số nhân có số hạng đầu $u_1=\frac{1}{2}$ và công bội $q=\frac{1}{2}$.

Khi đó công thức số hạng tổng quát là: $u_k={\left(\frac{1}{2}\right)}^k,\left(k=1,2,3,\mathrm{...}\right)$

b) Tổng diện tích S_n của phần hình được tô màu sau lần tô thứ n (n = 1, 2, 3, ...) là tổng n số hạng đầu của cấp số nhân ta được:

$S_n=\frac{u_1\left(1-q^n\right)}{1-q}=\frac{\frac{1}{2}.\left(1-{\left(\frac{1}{2}\right)}^n\right)}{1-\frac{1}{2}}=\left(1-{\left(\frac{1}{2}\right)}^n\right)$.

c) Ta có: limS_n = $\lim \left(1-{\left(\frac{1}{2}\right)}^n\right)=\lim 1-\lim {\left(\frac{1}{2}\right)}^n=1$.

Khi đó limS_n = 2u₁.

Giải Toán 11 trang 68 Tập 1

Thực hành 4 trang 68 Toán 11 Tập 1: Tính tổng của cấp số nhân lùi vô hạn: $1+\frac{1}{3}+{\left(\frac{1}{3}\right)}^2+\mathrm{...}+{\left(\frac{1}{3}\right)}^n+\mathrm{...}$

Lời giải:

Tổng của cấp số nhân lùi vô hạn có số hạng đầu u₁ = 1 và công bội là $q=\frac{1}{3}<1$ là:

$S_n=1+\frac{1}{3}+{\left(\frac{1}{3}\right)}^2+\mathrm{...}+{\left(\frac{1}{3}\right)}^n+\mathrm{...}=\frac{1}{1-\frac{1}{3}}=\frac{3}{2}$.

Vận dụng 1 trang 68 Toán 11 Tập 1: Từ tờ giấy, cắt một hình tròn bán kính R (cm) như Hình 3a. Tiếp theo, cắt hai hình tròn bán kính $\frac{R}{2}$ rồi chồng lên hình tròn đầu tiên như Hình 3b. Tiếp theo, cắt bốn hình tròn bán kính $\frac{R}{4}$ rồi chồng lên các hình trước như Hình 3c. Cứ thế tiếp tục mãi. Tính tổng diện tích của các hình tròn.

Lời giải:

Nội dung đang được cập nhật...

4. Giới hạn vô cực

Hoạt động khám phá 5 trang 68 Toán 11 Tập 1: Dựng một dãy hình vuông bằng cách ghép từ các hình vuông đơn vị (cạnh bằng 1 đơn vị độ dài) theo các bước như Hình 4. Kí hiệu u_n (đơn vị diện tích) là diện tích hình vuông dựng được ở bước thứ n.

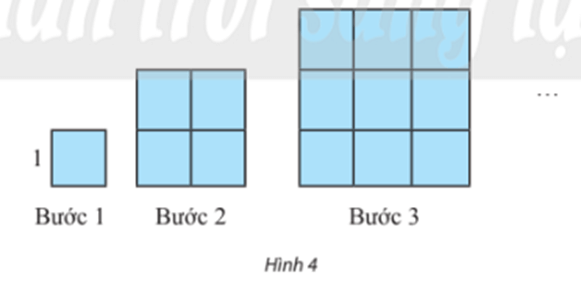
a) Với n như thế nào thì u_n vượt quá 10 000; 1 000 000?

b) Cho hình có diện tích S. Với n như thế nào thì u_n vượt quá S?

Lời giải:

a) Diện tích của hình vuông u_n dựng ở bước thứ n là: u_n = n² (đơn vị diện tích).

Để u_n vượt quá 10 000 thì n² > 10 000 ⇔ n > 100.

Để u_n vượt quá 1 000 000 thì n² > 1 000 000 ⇔ n > 1000.

b) Để u_n vượt quá S thì u_n > S ⇔ n² > S ⇔ n > $\sqrt{S}$.

Bài tập

Giải Toán 11 trang 69 Tập 1

Bài 1 trang 69 Toán 11 Tập 1: Tìm các giới hạn sau:

a) $\lim \frac{-2n+1}{n}$;

b) $\lim \frac{\sqrt{16n^2-2}}{n}$;

c) $\lim \frac{4}{2n+1}$;

d) $\lim \frac{n^2-2n+3}{2n^2}$.

Lời giải:

a) $\lim \frac{-2n+1}{n}=\lim \left(-2+\frac{1}{n}\right)=\lim \left(-2\right)+\lim \frac{1}{n}=-2$

b) $\lim \frac{\sqrt{16n^2-2}}{n}=\lim \sqrt{\frac{16n^2-2}{n^2}}=\sqrt{\lim \left(16-\frac{2}{n^2}\right)}=\sqrt{16}=4$;

c) $\lim \frac{4}{2n+1}=\lim \frac{\frac{4}{n}}{2+\frac{1}{n}}=\frac{0}{2+0}=0$;

d) $\lim \frac{n^2-2n+3}{2n^2}=\lim \frac{1-\frac{2}{n}+\frac{3}{n^2}}{2}=\frac{1}{2}$.

Bài 2 trang 69 Toán 11 Tập 1: Tính tổng của các cấp số nhân lùi vô hạn sau:

a) $-\frac{1}{2}+\frac{1}{4}-\frac{1}{8}+\mathrm{...}+{\left(-\frac{1}{2}\right)}^n+\mathrm{...}$;

b) $\frac{1}{4}+\frac{1}{16}+\frac{1}{64}+\mathrm{...}+{\left(\frac{1}{4}\right)}^n+\mathrm{...}$ .

Lời giải:

a) Tổng của cấp số nhân lùi vô hạn với số hạng đầu $u_1=-\frac{1}{2}$ và công bội $q=-\frac{1}{2}$ bằng:$S=-\frac{1}{2}+\frac{1}{4}-\frac{1}{8}+\mathrm{...}+{\left(-\frac{1}{2}\right)}^n+\mathrm{...}=\frac{u_1}{1-q}=\frac{-\frac{1}{2}}{1-\left(-\frac{1}{2}\right)}=-\frac{1}{3}$.

b) Tổng của cấp số nhân lùi vô hạn với số hạng đầu $u_1=\frac{1}{4}$ và công bội $q=\frac{1}{4}$bằng: $S=\frac{1}{4}+\frac{1}{16}+\frac{1}{64}+\mathrm{...}+{\left(\frac{1}{4}\right)}^n+\mathrm{...}=\frac{\frac{1}{4}}{1-\frac{1}{4}}=\frac{1}{3}$.

Bài 3 trang 69 Toán 11 Tập 1: Viết số thập phân vô hạn tuần hoàn 0,444 ... dưới dạng phân số.

Lời giải:

Ta có: 0,444... = 0,(4) = $\frac{4}{9}$.

Giải Toán 11 trang 70 Tập 1

Bài 4 trang 70 Toán 11 Tập 1: Từ hình vuông đầu tiên có cạnh bằng 1 (đơn vị độ dài), nối các trung điểm của bốn cạnh để có hình vuông thứ hai. Tiếp tục nối các trung điểm của bốn cạnh của hình vuông thứ hai để được hình vuông thứ ba. Cứ tiếp tục làm như thế, nhận được một dãy hình vuông (xem Hình 5).

a) Kí hiệu a_n là diện tích của hình vuông thứ n và S_n là tổng diện tích của n hình vuông đầu tiên. Viết công thức tính a_n, S_n (n = 1, 2, 3, ...) và tìm limS_n (giới hạn này nếu có được gọi là tổng diện tích của các hình vuông).

b) Kí hiệu p_n là chu vi của hình vuông thứ n và Q_n là tổng chu vi của n hình vuông đầu tiên. Viết công thức tính p_n và Q_n (n = 1, 2, 3, ...) và tìm limQ_n (giới hạn này nếu có được gọi là tổng chu vi của các hình vuông).

Lời giải:

a) Diện tích của các hình vuông lập thành một cấp số nhân lùi vô hạn (a_n) với số hạng đầu là u₁ = 1 và công bội $\frac{1}{2}$ nên công thức tổng quát của a_n = ${\left(\frac{1}{2}\right)}^{n-1}$.

Ta có: $S_n=1+\frac{1}{2}+\frac{1}{4}+\mathrm{...}+\frac{1}{2^n}+\mathrm{...}$

Tổng cấp số nhân lùi vô hạn là: $S=\lim S_n=\lim \left(1+\frac{1}{2}+\frac{1}{4}+\mathrm{...}+\frac{1}{2^n}+\mathrm{...}\right)=\frac{1}{1-\frac{1}{2}}=2$.

b) Chu vi p_n của hình vuông lập thành một cấp số nhân lùi vô hạn với số hạng đầu u₁ = 4 và công bội q = $\frac{1}{2}$ có số hạng tổng quát là: $p_n=4{\left(\frac{1}{2}\right)}^{n-1}$.

Ta có: $Q_n=4+4.\frac{1}{2}+4.\frac{1}{4}+\mathrm{...}+4.\frac{1}{2^n}+\mathrm{...}$

Tổng của cấp số nhân lùi vô hạn là: $Q=\lim Q_n=\lim \left(4+4.\frac{1}{2}+4.\frac{1}{4}+\mathrm{...}+4.\frac{1}{2^n}+\mathrm{...}\right)=\frac{4}{1-\frac{1}{2}}=8$.

Bài 5 trang 70 Toán 11 Tập 1: Xét quá trình tạo ra hình có chu vi vô cực và diện tích bằng 0 như sau:

a) Bắt đầu một hình vuông H­₀ cạnh bằng 1 đơn vị độ dài (xem Hình 6a). Chia hình vuông H₀ thành chín hình vuông bằng nhau, bỏ đi bốn hình vuông, nhận được hình H₁ (xem Hình 6b). Tiếp theo, chia mỗi hình vuông của H₁ thành chín hình vuông, rồi bỏ đi bốn hình vuông, nhận được hình H₂ (xem Hình 6c). Tiếp tục quá trình này ta nhận được một dãy hình H_n(n = 1, 2, 3, ...).

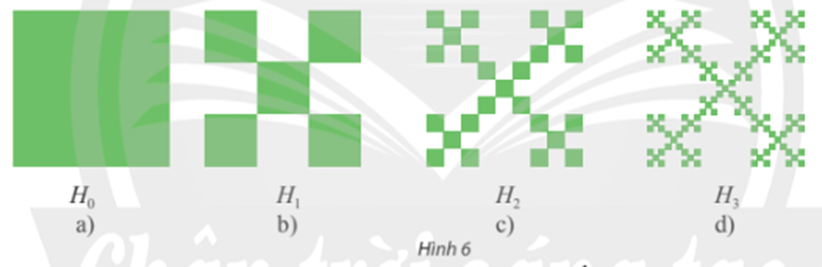
Ta có: H₁ có 5 hình vuông, mỗi hình vuông có cạnh bằng $\frac{1}{3}$;

H₂ có 5.5 = 5² hình vuông, mỗi hình vuông có cạnh bằng $\frac{1}{3}.\frac{1}{3}=\frac{1}{3^2};\mathrm{...}$

Từ đó, nhận được H_n có 5ⁿ hình vuông, mỗi hình vuông có cạnh bằng $\frac{1}{3^n}$.

a) Tính diện tích S_n của H_n và tính lim S_n.

b) Tính chu vi p_n của H_n và tính limp_n.

(Quá trình trên tạo nên một hình, gọi là một fractal, được coi là có diện tích lim S_n và chu vi limp_n).

Lời giải:

a) Diện tích S_n của H_n là $S_n=5^n.{\left(\frac{1}{3}\right)}^n.{\left(\frac{1}{3}\right)}^n=5^n.{\left(\frac{1}{3}\right)}^{2n}={\left(\frac{5}{9}\right)}^n$

Khi đó ${\text{limS}}_n=\lim {\left(\frac{5}{9}\right)}^n=0$.

b) Chu vi p_n của H_n là: $p_n=5^n.\left(4.\frac{1}{3^n}\right)=4.{\left(\frac{5}{3}\right)}^n$.

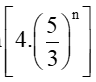
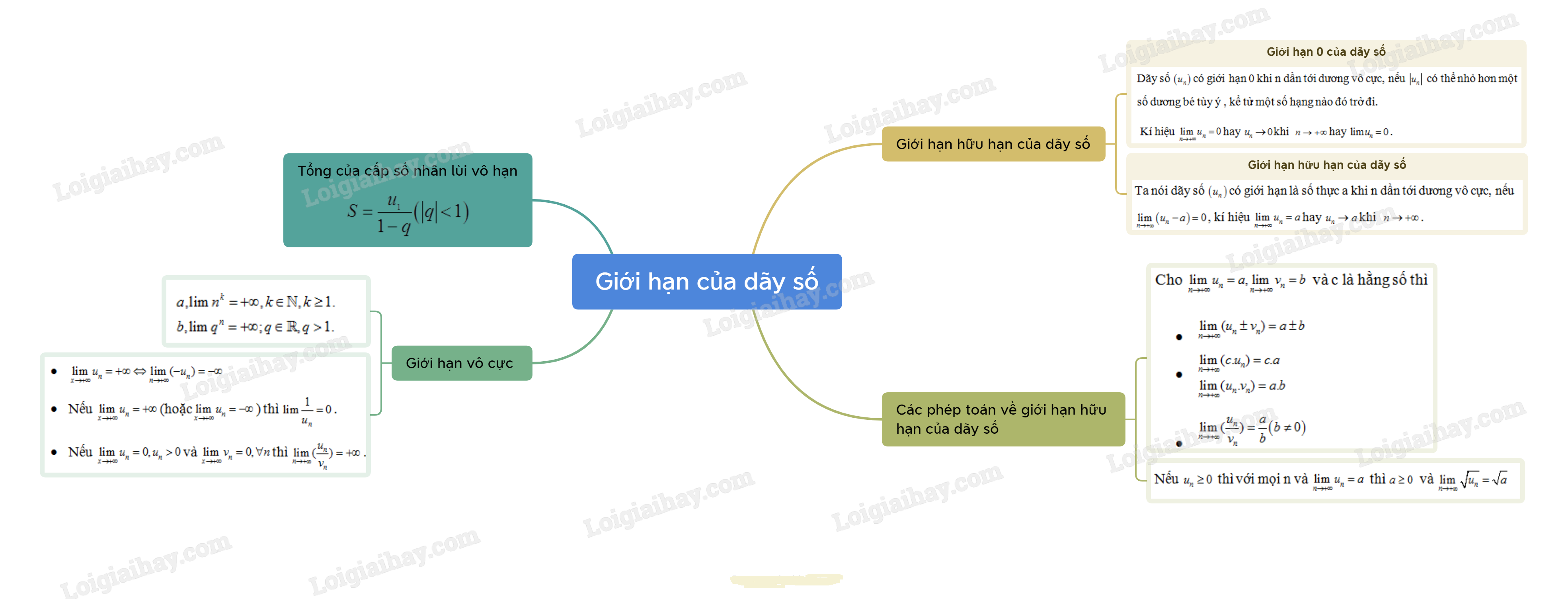
Khi đó limp_n = lim = 0.

Lý thuyết Giới hạn của dãy số

1. Giới hạn hữu hạn của dãy số

a, Giới hạn 0 của dãy số

- Dãy số $\left(u_n\right)$ có giới hạn 0 khi n dần tới dương vô cực, nếu $\left|u_n\right|$ có thể nhỏ hơn một số dương bé tùy ý , kể tử một số hạng nào đó trở đi.

Kí hiệu $\underset{n\to +\mathrm{\infty }}{lim}{u}_n=0$ hay $u_n\to 0$khi $n\to +\mathrm{\infty }$ hay $lim{u}_n=0$.

* Chú ý:

+ $lim\frac{1}{n^k}=0,k\in \mathbb{Z}.$

+ Nếu $\left|q\right|<1$ thì $lim{q}^n=0$

b, Giới hạn hữu hạn của dãy số

Ta nói dãy số $\left(u_n\right)$ có giới hạn là số thực a khi n dần tới dương vô cực, nếu $\underset{n\to +\mathrm{\infty }}{lim}\left(u_n-a\right)=0$, kí hiệu $\underset{n\to +\mathrm{\infty }}{lim}{u}_n=a$ hay $u_n\to a$ khi $n\to +\mathrm{\infty }$.

* Chú ý: Nếu $u_n=c$(c là hằng số) thì $\underset{n\to +\mathrm{\infty }}{lim}{u}_n=c$

2. Các phép toán về giới hạn hữu hạn của dãy số

Cho $\underset{n\to +\mathrm{\infty }}{lim}{u}_n=a,\underset{n\to +\mathrm{\infty }}{lim}{v}_n=b$ và c là hằng số thì

• $\underset{n\to +\mathrm{\infty }}{lim}(u_n\pm v_n)=a\pm b$
• $\begin{array}{l}\underset{n\to +\mathrm{\infty }}{lim}(c.u_n)=c.a\\ \underset{n\to +\mathrm{\infty }}{lim}(u_n.v_n)=a.b\end{array}$
• $\underset{n\to +\mathrm{\infty }}{lim}(\frac{u_n}{v_n})=\frac{a}{b}\left(b\ne 0\right)$
• Nếu $u_n\ge 0$ thì với mọi n và $\underset{n\to +\mathrm{\infty }}{lim}{u}_n=a$ thì $a\ge 0$ và $\underset{n\to +\mathrm{\infty }}{lim}\sqrt{u_n}=\sqrt{a}$

3. Tổng của cấp số nhân lùi vô hạn

Cấp số nhân $\left(u_n\right)$ có công bội q thỏa mãn $\left|q\right|<1$ được gọi là cấp số nhân lùi vô hạn.

Tổng của cấp số nhân lùi vô hạn là:

$S=\frac{u_1}{1-q}\left(\left|q\right|<1\right)$

4. Giới hạn vô cực

- Dãy số $\left(u_n\right)$được gọi là có giới hạn $+\mathrm{\infty }$khi $n\to +\mathrm{\infty }$nếu $u_n$ có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi, kí hiệu $\underset{x\to +\mathrm{\infty }}{lim}{u}_n=+\mathrm{\infty }$ hay $u_n\to +\mathrm{\infty }$ khi $n\to +\mathrm{\infty }$.

- Dãy số $\left(u_n\right)$ được gọi là có giới hạn $-\mathrm{\infty }$khi $n\to +\mathrm{\infty }$ nếu $\underset{x\to +\mathrm{\infty }}{lim}\left(-u_n\right)=+\mathrm{\infty }$, kí hiệu $\underset{x\to +\mathrm{\infty }}{lim}{u}_n=-\mathrm{\infty }$ hay $u_n\to -\mathrm{\infty }$ khi $n\to +\mathrm{\infty }$.

* Chú ý:

• $\underset{x\to +\mathrm{\infty }}{lim}{u}_n=+\mathrm{\infty }\iff \underset{n\to +\mathrm{\infty }}{lim}(-u_n)=-\mathrm{\infty }$
• Nếu $\underset{x\to +\mathrm{\infty }}{lim}{u}_n=+\mathrm{\infty }$(hoặc$\underset{x\to +\mathrm{\infty }}{lim}{u}_n=-\mathrm{\infty }$) thì $lim\frac{1}{u_n}=0$.
• Nếu $\underset{x\to +\mathrm{\infty }}{lim}{u}_n=0,u_n>0$và $\underset{x\to +\mathrm{\infty }}{lim}{v}_n=0,\mathrm{\forall }n$thì $\underset{n\to +\mathrm{\infty }}{lim}(\frac{u_n}{v_n})=+\mathrm{\infty }$.

*Nhận xét:

$\begin{array}{l}a,lim{n}^k=+\mathrm{\infty },k\in \mathbb{N},k\ge 1.\\ b,lim{q}^n=+\mathrm{\infty };q\in \mathbb{R},q>1.\end{array}$

Xem thêm lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 2

Bài 2: Giới hạn của hàm số

Bài 3: Hàm số liên tục

Bài tập cuối chương 3

Bài 1: Điểm, đường thẳng và mặt phẳng trong không gian