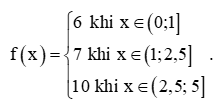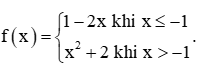Toán 11 Bài 2 (Chân trời sáng tạo): Giới hạn của hàm số
Với giải bài tập Toán lớp 11 Bài 2: Giới hạn của hàm số sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 11 Bài 2.
Giải Toán 11 Bài 2: Giới hạn của hàm số
Bài giảng Toán 11 Bài 2: Giới hạn của hàm số
Lời giải:
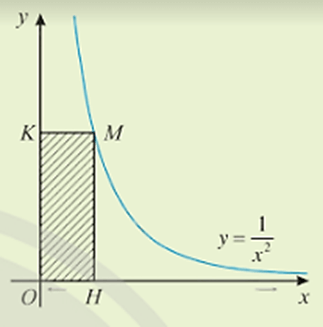
Hình chữ nhật OHMK có các kích thước lần lượt là hoành độ và tung độ của điểm M.
Ta có: điểm M luôn nằm trên đồ thị y=1x2(x>0)
Đặt M(x;1x2)(x>0)
Khi đó diện tích hình chữ nhật OHMK là: x.1x2=1x.
Khi H gần tiến đến gốc tọa độ nghĩa là x dần tiến tới 0 thì diện tích hinh chữ nhật sẽ là một số rất lớn.
Khi H iến xa sang phía bên phải thì x dần tiến tới +∞ thì diện tích hình chữ nhật sẽ giảm dần về 0.
1. Giới hạn hữu hạn của hàm số tại một điểm
Hoạt động khám phá 1 trang 71 Toán 11 Tập 1: Xét hàm số y=f(x)=2x2−2x−1
a) Bảng sau đây cho biết giá trị của hàm số tại một số điểm gần điểm 1.
Có nhận xét gì về giá trị của hàm số khi x càng gần đến 1?
Lời giải:
a) Khi x càng gần đến 1 thì giá trị của f(x) gần đến giá trị 4.
b) Khi điểm H thay đổi gần về điểm (1; 0) trên trục hoàng thì điểm P gần về điểm (0; 4).
Thực hành 1 trang 72 Toán 11 Tập 1: Tìm các giới hạn sau:
Lời giải:
a) Hàm số f(x) = 2x2 – x xác định trên ℝ.
Giả sử (xn) là dãy số bất kì, thỏa mãn xn ∈ ℝ với mọi n và xn → 3 khi n → +∞. Ta có: limxn→3(2x2n−xn)=limxn→3(2x2n)−limxn→3(xn)=2.32−3=15.
Vậy limx→3(2x2−x)=15.
b) Hàm số f(x)=x2+2x+1x+1 xác định trên tập ℝ\{– 1}.
Giả sử (xn) là dãy số bất kì, thỏa mãn xn ∈ ℝ\{– 1} với mọi n và xn → – 1 khi n → +∞.
Ta có:
limxn→−1x2n+2xn+1xn+1=limxn→−1(xn+1)2xn+1=limxn→−1(xn+1)=limxn→−1xn+1=(−1)+1=0
Vậy limx→−1x2+2x+1x+1=0.
2. Các phép toán về giới hạn hữu hạn của hàm số
Hoạt động khám phá 2 trang 72 Toán 11 Tập 1: Cho hai hàm số y = f(x) = 2x và y = g(x) = xx+1.
b) Từ đó, tìm giới hạn limx→1[f(x)+g(x)], và so sánh với limx→1f(x)+limx→1g(x).
Lời giải:
+) Hàm số y = f(x) = 2x xác định trên ℝ.
Dãy số (xn) bất kì thỏa mãn xn ≠ – 1 với mọi n và xn → 1 khi n → +∞, ta có:
limf(xn) = lim(2xn) = 2.limxn = 2.1 = 2.
Suy ralimx→1f(x) = 2.
+) Hàm số y = g(x) = xx+1 xác định trên ℝ \ {2}.
Dãy số (xn) bất kì thỏa mãn xn ≠ – 1 với mọi n và xn → 1 khi n → +∞, ta có:
limg(xn) =limxnxn+1=12.
Suy ra limx→−1g(x)=12.
a) Ta có: lim[f(xn) + g(xn)] = limf(xn) + limg(xn) = 2+12=52.
b) Ta có lim[f(xn)+g(xn)]=52 nên limx→1[f(x)+g(x)]=52.
Ta lại có: limx→1f(x)+limx→1g(x)=2+12=52.
Vì vậy limx→1[f(x)+g(x)]=limx→1f(x)+limx→1g(x).
Thực hành 2 trang 73 Toán 11 Tập 1: Tìm các giới hạn sau:
Lời giải:
a)
limx→−2(x2+5x−2)=limx→−2x2+limx→−25x+limx→−2(−2)=(−2)2+5.(−2)−2=−8
b) limx→1x2−1x−1=limx→1(x−1)(x+1)x−1=limx→1(x+1)=2.
3. Giới hạn một phía
a) Giả sử (xn) là dãy số bất kì sao cho xn ∈ (1; 2,5) và lim xn = 1. Tìm lim f(xn).
b) Giả sử (x'n) là dãy số bất kì sao cho (x'n)∈(0;1) và limx'n=1. Tìm limf(x'n).
c) Nhận xét về kết quả ở a) và b).
Lời giải:
a) Giả sử (xn) là dãy số bất kì sao cho xn ∈ (1; 2,5) và lim xn = 1 thì lim f(xn) = lim 7 = 7.
b) Giả sử (x'n) là dãy số bất kì sao cho (x'n)∈(0;1) và limx'n=1 thì limf(x'n)=6.
c) Nhận xét: Ở ý a) ta có:
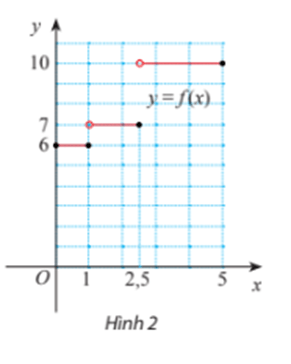
Thực hành 3 trang 75 Toán 11 Tập 1: Cho hàm số
Tìm các giới hạn limx→−1+f(x),limx→−1−f(x) và limx→−1f(x) (nếu có).
Lời giải:
+) Với dãy số (xn) bất kì, xn ≤ – 1 và xn → – 1. Khi đó f(xn) = 1 – 2xn nên limf(xn) = lim(1 – 2xn) = 3.
Vì vậy limx→−1−f(x)=3.
+) Với dãy số (xn) bất kì, xn > – 1 và xn → – 1. Khi đó f(xn) = x2n+2 nên limf(xn) = lim(x2n+2) = 3.
Vì vậy limx→−1+f(x)=3.
Vì limx→−1+f(x)=limx→−1−f(x)=3 nên limx→−1f(x)=3.
4. Giới hạn hữu hạn của hàm số tại vô cực
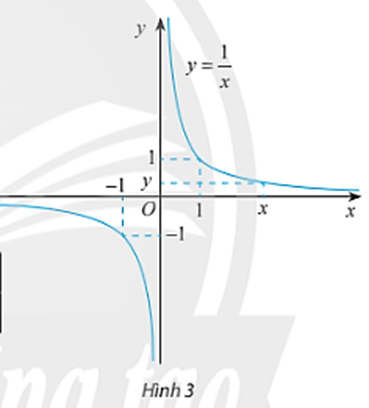
Hoạt động khám phá 4 trang 75 Toán 11 Tập 1: Cho hàm số f(x)=1x có đồ thị như Hình 3.
a) Tìm các giá trị còn thiếu trong bảng sau:
Từ đồ thị và bảng trên, nêu nhận xét về giá trị f(x) khi x càng lớn (dần tới +∞)?
b) Tìm các giá trị còn thiếu trong bảng sau:
Từ đồ thị và bảng trên, nêu nhận xét về giá trị f(x) khi x càng bé (dần tới – ∞)?
Lời giải:
a) Với x = 1 000 suy ra y=11000=0,001;
Với x = 10 000 suy ra y=110000=0,0001;
Với x = 100 000 suy ra y=1100000=0,00001.
Từ đó ta có bảng sau:
|
x |
10 |
100 |
1 000 |
10 000 |
100 000 |
|
y = f(x) |
0,1 |
0,01 |
0,001 |
0,0001 |
0,00001 |
b) Với x = – 100 000 suy ra y=1−100000=0,00001;
Với x = – 10 000 suy ra y=1−10000=−0,0001;
Với x = – 1 000 suy ra y=1−1000=−0,001.
Từ đó ta có bảng sau:
|
x |
– 100 000 |
– 10 000 |
– 1 000 |
– 100 |
– 10 |
|
y = f(x) |
–0,00001 |
–0,0001 |
–0,001 |
–0,01 |
–0,1 |
Thực hành 4 trang 76 Toán 11 Tập 1: Tìm các giới hạn sau:
Lời giải:
a) limx→+∞1−3x2x2+2x=limx→+∞1x2−31+2x=−3
b) limx→−∞2x+1=limx→−∞2x1+1x=0.
a) Viết biểu thức C(t) biểu thị nồng độ muối trong hồ sau t phút kể từ khi bắt đầu bơm.
b) Tìm giới hạn limx→+∞C(t) và giải thích ý nghĩa.
Lời giải:
a) Trong 200m3 nước có nồng độ muối là 10kg/m3.
Do đó trong 200 m3 nước có 10.200 = 2000 kg muối.
Mỗi phút người ta bơm nước ngọt vào hồ 2m3 thì sau t phút có 200 + 2t (m3).
Khi đó nồng độ muối trong bể là:C(t)=2000200+x(kg/m3).
b) limt→+∞C(t)=limt→+∞2000200+2t=limt→+∞2000t200t+2=0.
Vậy khi bom nước ngọt vào hồ thì phải mất rất nhiều thời gian hồ mới được ngọt hóa.
5. Giới hạn vô cực của hàm số tại một điểm
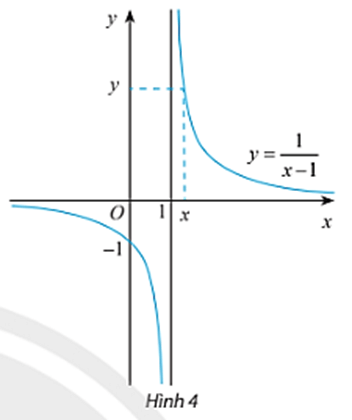
Hoạt động khám phá 5 trang 77 Toán 11 Tập 1: Cho hàm số f(x)=1x−1 có đồ thị như Hình 4.
a) Tìm các giá trị còn thiếu trong bảng sau:
Từ đồ thị và bảng trên, có nhận xét gì về giá trị f(x) khi x dần tới 1 phía bên phải?
b) Tìm các giá trị còn thiếu trong bảng sau:
Từ đồ thị và bảng trên, có nhận xét gì về giá trị f(x) khi x dần tới 1 phía bên trái?
Lời giải:
a) Với x = 1,001 thì y = f(x) = 1x−1=11,001−1=1000;
Với x = 1,0001 thì y = f(x) = 1x−1=11,0001−1=10000.
Khi đó ta có bảng:
|
x |
1,1 |
1,01 |
1,001 |
1,0001 |
|
y = f(x) |
10 |
100 |
1 000 |
10 000 |
Nhận xét: Khi x dần tới 1 phía bên phải thì f(x) tăng dần tới một giá trị rất lớn (dương vô cực).
b) Với x = 0,999 thì y = f(x) = 1x−1=10,999−1=−1000;
Với x = 1,0001 thì y = f(x) = 1x−1=10,9999−1=−10000.
Khi đó ta có bảng:
|
x |
0,9 |
0,99 |
0,999 |
0,9999 |
|
y = f(x) |
– 10 |
– 100 |
– 1 000 |
– 10 000 |
Nhận xét: Khi x dần tới 1 phía bên phải thì f(x) giảm dần tới một giá trị rất nhỏ (âm vô cực).
Thực hành 5 trang 78 Toán 11 Tập 1: Tìm các giới hạn sau:
Lời giải:
a) Ta có: limx→3−2x=6;limx→3−1x−3=−∞
Do đó limx→3−2xx−3=limx→3−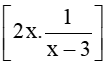
b) Ta có: 3x – 1 = x(3−1x)
Suy ra limx→+∞(3x−1)=limx→+∞x(3−1x)=limx→+∞x.limx→+∞(3−1x)=+∞.
Lời giải:
Hình chữ nhật OHMK có các kích thước lần lượt là hoành độ và tung độ của điểm M.
Ta có x là hoành độ điểm H nên hoành độ điểm M cũng bằng x và M luôn nằm trên đồ thị y=1x2(x>0) nên tọa độ điểm M là (x;1x2)(x>0).
Khi đó diện tích hình chữ nhật OHMK là:x.1x2=1x.
Khi H gần tiến đến gốc tọa độ nghĩa là x dần tiến đến 0+ thì limx→0+1x=+∞.
Khi H tiến xa sang phía bên phải thì x dần tiến tới +∞ thì limx→+∞1x=0.
Bài tập
Bài 1 trang 79 Toán 11 Tập 1: Tìm các giới hạn sau:
Lời giải:
a)
limx→−2(x2−7x+4)=limx→−2x2−7.limx→−2x+limx→−24=4−7.(−2)+4=22.
b) limx→3x−3x2−9=limx→3x−3(x−3)(x+3)=limx→31x+3=16
c)
limx→13−√x+8x−1=limx→1(3−√x+8)(3−+√x+8)(x−1)(3−√x+8)=limx→19−x−8(x−1)(3+√x+8)
=limx→1−13+√x+8=−16.
Bài 2 trang 79 Toán 11 Tập 1: Cho hàm số 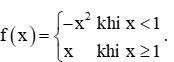
Tìm các giới hạn sau: limx→1+f(x);limx→1−f(x);limx→1f(x) (nếu có).
Lời giải:
+) Với dãy số (xn) bất kì, xn ≤ 1 và xn → 1. Khi đó f(xn) = −x2n nên limf(xn) = lim(−x2n)=−1.
Vì vậy limx→1−f(x)=−1.
+) Với dãy số (xn) bất kì, xn > 1 và xn → 1. Khi đó f(xn) = xn nên limf(xn) = lim(xn) = 1.
Vì vậy limx→1+f(x)=1.
+) Vì limx→1+f(x)≠limx→1−f(x) nên không tồn tại limx→1f(x).
Bài 3 trang 79 Toán 11 Tập 1: Tìm các giới hạn sau:
Lời giải:
a) limx→+∞4x+32x=limx→+∞4+3x2=2.
b) limx→−∞23x+1=limx→−∞2x3+1x=0.
c) limx→+∞√x2+1x+1=limx→+∞√x2+1x+1=limx→+∞√1+1x21+1x=1.
Bài 4 trang 79 Toán 11 Tập 1: Tìm các giới hạn sau:
Lời giải:
a) limx→−1+1x+1=limx→−1+1x1+1x=0;
b) Ta viết: 1−x2=x2.(1x2−1)
Ta có: limx→−∞x2=+∞;limx→−∞(1x2−1)=−1
Do đó: limx→−∞(1−x2)=limx→−∞x2(1x2−1)=−∞.
c) Ta viết: x3−x=x.13−x
Ta có: limx→3+x=3;limx→3+13−x=+∞
Do đó: limx→3+x3−x=limx→3+(x.13−x)=limx→3+x.limx→3+13−x=+∞.
b) Nồng độ muối như thế nào nếu t → +∞.
Lời giải:
a) Sau t phút số lít nước biển bơm vào là: 15t (lít).
Khi đó số gam muối trong 15t lít nước biển là: 30.15t (gam).
Tổng số lít nước trong hồ là: 6000 + 15t (lít).
Nồng độ muối của nước trong hồ sau t phút kể từ khi bắt đầu bơm là: C(t)=30.15t6000+15t=30t400+t (gam/lít).
b) Khi t → +∞ thì limt→+∞C(t)=limt→+∞30t400+t=limt→+∞30400t+1=30.
Vậy nồng độ muối trong hồ gần đến 30gam/lít khi t → +∞.
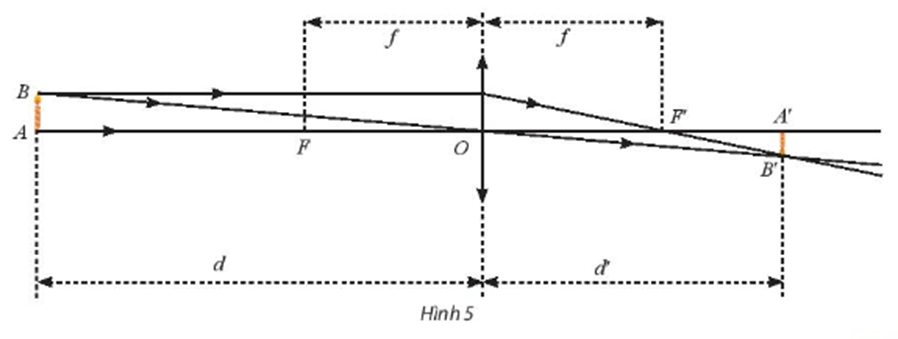
Xét hàm số g(d)=dfd−f. Tìm các giới hạn sau đây và giải thích ý nghĩa.
Lời giải:
a) Ta có: limd→f+g(d)=limd→f+dfd−f=limd→f+df.limd→f+1d−f=+∞.
Như vậy khi khoảng cách của vật đến quang tâm O gần bằng tiêu cự của thấu kính thì khoảng cách từ ảnh đến quang tâm O của thấu kính càng lớn.
b) Ta có: limd→+∞g(d)=limd→+∞dfd−f=limd→+∞f1−fd=f.
Như vậy khi khoảng cách của vật đến quang tâm O càng lớn thì khoảng cách từ ảnh đến quang tâm O của thấu kính càng gần tiêu cự.
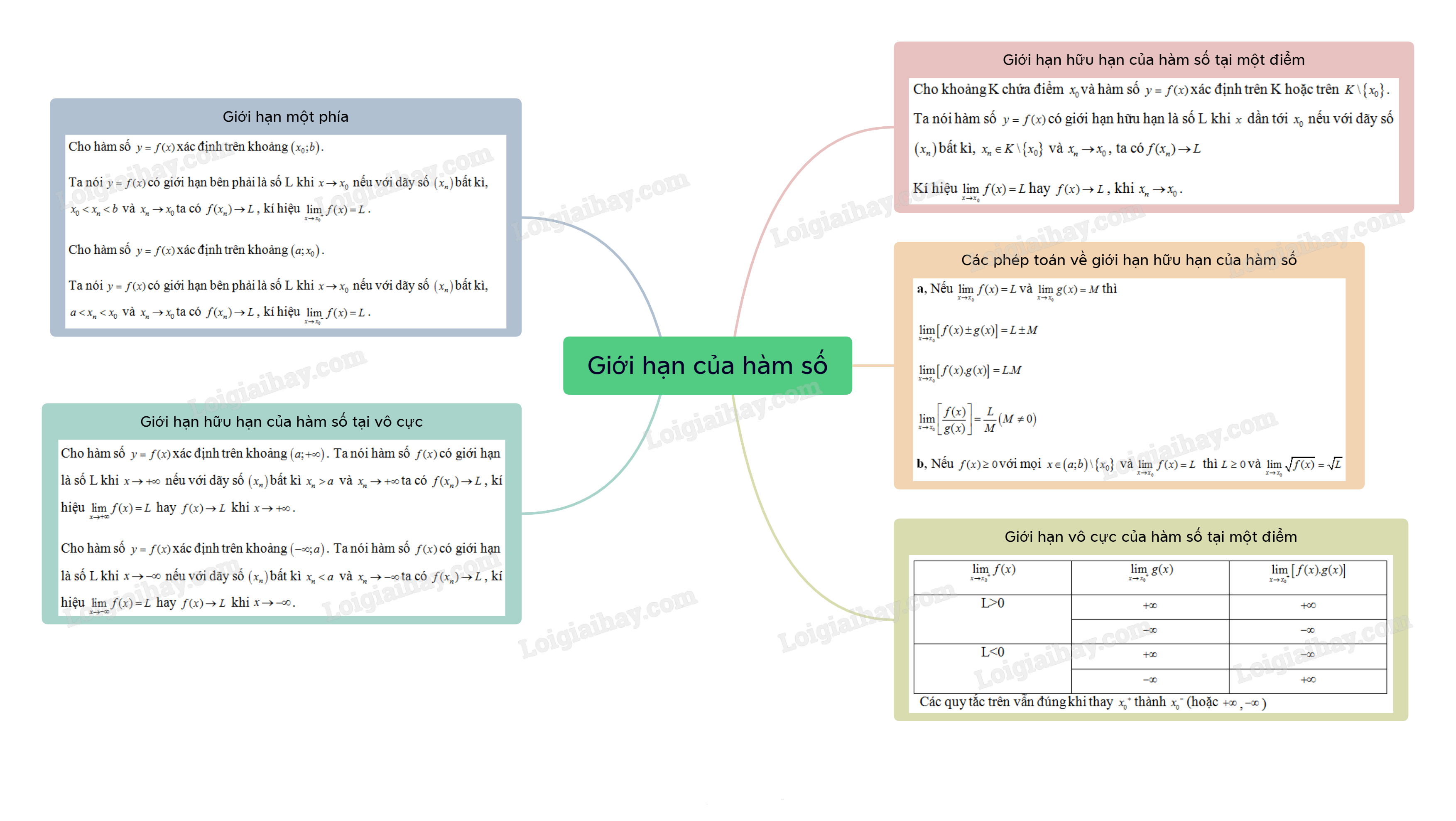
Lý thuyết Giới hạn của hàm số
1. Giới hạn hữu hạn của hàm số tại một điểm
Cho khoảng K chứa điểm x0và hàm số y=f(x) xác định trên K hoặc trên K∖{x0}. Ta nói hàm số y=f(x) có giới hạn hữu hạn là số L khi x dần tới x0 nếu với dãy số (xn) bất kì, xn∈K∖{x0} và xn→x0, ta cóf(xn)→L
Kí hiệu limx→x0f(x)=L hay f(x)→L, khi xn→x0.
2. Các phép toán về giới hạn hữu hạn của hàm số
a, Nếu limx→x0f(x)=L và limx→x0g(x)=M thì
limx→x0[f(x)±g(x)]=L±M
limx→x0[f(x).g(x)]=L.M
limx→x0[f(x)g(x)]=LM(M≠0)
b, Nếu f(x)≥0 với mọi x∈(a;b)∖{x0} và limx→x0f(x)=L thì L≥0và limx→x0√f(x)=√L.
* Nhận xét:
a,limx→x0xk=x0k,k∈Z+.b,limx→x0[c.f(x)]=c.limx→x0f(x)
(c∈R, nếu tồn tại limx→x0f(x)∈R)
3. Giới hạn một phía
Cho hàm số y=f(x) xác định trên khoảng (x0;b).
Ta nói y=f(x) có giới hạn bên phải là số L khi x→x0 nếu với dãy số (xn) bất kì,x0<xn<b và xn→x0ta có f(xn)→L, kí hiệu limx→x0+f(x)=L.
Cho hàm số y=f(x) xác định trên khoảng (a;x0).
Ta nói y=f(x)có giới hạn bên phải là số L khi x→x0 nếu với dãy số (xn)bất kì,a<xn<x0 và xn→x0ta có f(xn)→L, kí hiệu limx→x0−f(x)=L.
*Chú ý:
limx→x0f(x)=L⇔limx→x0−f(x)=limx→x0+f(x)=L
limx→x0−f(x)≠limx→x0+f(x) thì không tồn tại limx→x0f(x).
Các phép toán về giới hạn hữu hạn của hàm số ở Mục 2 vẫn đúng khi ta thay x→x0bằng x→x0+hoặc x→x0−.
4. Giới hạn hữu hạn của hàm số tại vô cực
Cho hàm số y=f(x) xác định trên khoảng (a;+∞). Ta nói hàm số f(x)có giới hạn là số L khi x→+∞ nếu với dãy số (xn) bất kì xn>a và xn→+∞ta có f(xn)→L, kí hiệu limx→+∞f(x)=L hay f(x)→L khi x→+∞.
Cho hàm số y=f(x) xác định trên khoảng (−∞;a). Ta nói hàm số f(x) có giới hạn là số L khi x→−∞ nếu với dãy số (xn) bất kì xn<a và xn→−∞ta có f(xn)→L, kí hiệu limx→−∞f(x)=L hay f(x)→L khi x→−∞.
* Nhận xét:
- Các quy tắc tính giới hạn hữu hạn tại một điểm cũng đúng cho giới hạn hữu hạn tại vô cực.
- Với c là hằng số, k là một số nguyên dương ta có:
limx→±∞c=c,limx→±∞(cxk)=0
5. Giới hạn vô cực của hàm số tại một điểm
- Cho hàm số y=f(x)xác định trên khoảng (x0;b).
Ta nói hàm số f(x) có giới hạn bên phải là +∞ khi x→x0 về bên phải nếu với dãy số (xn) bất kì thỏa mãn x0<xn<b và xn→x0 ta có f(xn)→+∞, kí hiệu limx→x0+f(x)=+∞
Ta nói hàm số f(x) ó giới hạn bên phải là −∞ khi x→x0 về bên trái nếu với dãy số (xn) bất kì thỏa mãn a<xn<x0 và xn→x0 ta có f(xn)→+∞, kí hiệu limx→x0−f(x)=+∞
Các giới hạn một bênlimx→x0+f(x)=−∞, limx→x0−f(x)=−∞ được định nghĩa tương tự.
* Chú ý:
- limx→+∞xk=+∞,k∈Z+.
- limx→−∞xk=+∞, k là số nguyên dương chẵn.
- limx→−∞xk=−∞, k là số nguyên dương lẻ.
- limx→a+1x−a=+∞,limx→a−1x−a=−∞(a∈R)
Giới hạn vô cực
Nếu limx→x0+f(x)=L≠0 và limx→x0+g(x)=+∞hoặc limx→x0+g(x)=−∞thì limx→x0+[f(x).g(x)] được tính như sau:

Các quy tắc trên vẫn đúng khi thay x0+thành x0−(hoặc +∞,−∞)
Xem thêm lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Chân trời sáng tạo (hay nhất)
- Văn mẫu lớp 11 - Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn 11 – Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn lớp 11 - Chân trời sáng tạo
- Giải SBT Ngữ văn 11 – Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Ngữ văn 11 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Chân trời sáng tạo
- Soạn văn 11 Chân trời sáng tạo (ngắn nhất)
- Giải sgk Tiếng Anh 11 – Friends Global
- Giải sbt Tiếng Anh 11 - Friends Global
- Trọn bộ Từ vựng Tiếng Anh 11 Friends Global đầy đủ nhất
- Bài tập Tiếng Anh 11 Friends Global theo Unit có đáp án
- Giải sgk Vật lí 11 – Chân trời sáng tạo
- Lý thuyết Vật lí 11 – Chân trời sáng tạo
- Giải sbt Vật lí 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Vật lí 11 – Chân trời sáng tạo
- Giải sgk Hóa học 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Hóa học 11 – Chân trời sáng tạo
- Lý thuyết Hóa 11 - Chân trời sáng tạo
- Giải sbt Hóa học 11 – Chân trời sáng tạo
- Giải sgk Sinh học 11 – Chân trời sáng tạo
- Lý thuyết Sinh học 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Sinh học 11 – Chân trời sáng tạo
- Giải sbt Sinh học 11 – Chân trời sáng tạo
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Chân trời sáng tạo
- Lý thuyết Kinh tế pháp luật 11 – Chân trời sáng tạo
- Giải sbt Kinh tế pháp luật 11 – Chân trời sáng tạo
- Giải sgk Lịch sử 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Lịch sử 11 – Chân trời sáng tạo
- Lý thuyết Lịch sử 11 - Chân trời sáng tạo
- Giải sbt Lịch sử 11 – Chân trời sáng tạo
- Giải sgk Địa lí 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Địa lí 11 – Chân trời sáng tạo
- Lý thuyết Địa lí 11 - Chân trời sáng tạo
- Giải sbt Địa lí 11 – Chân trời sáng tạo
- Giải sgk Hoạt động trải nghiệm 11 – Chân trời sáng tạo