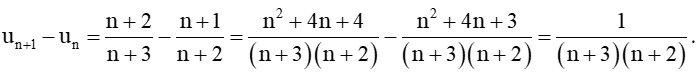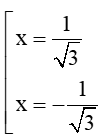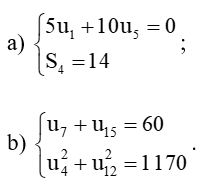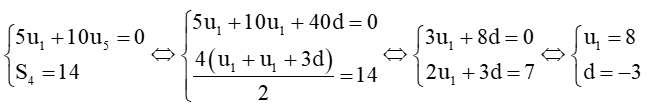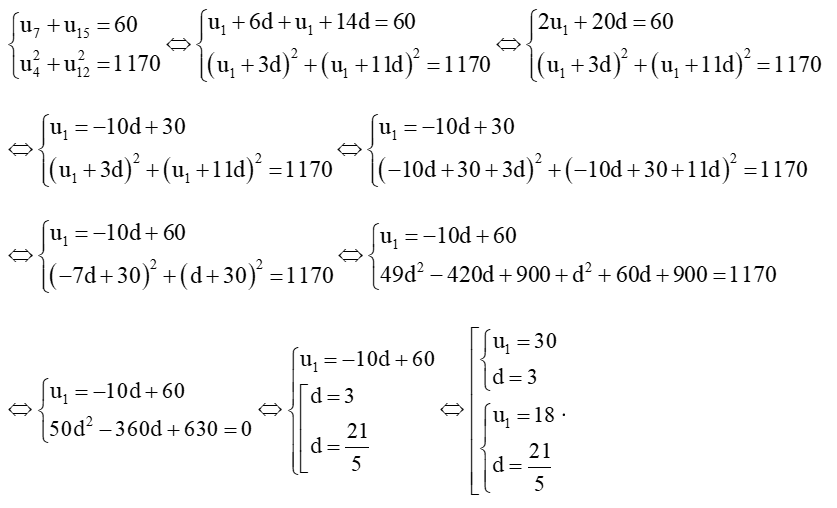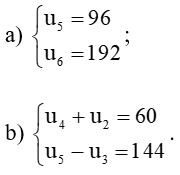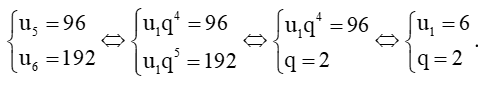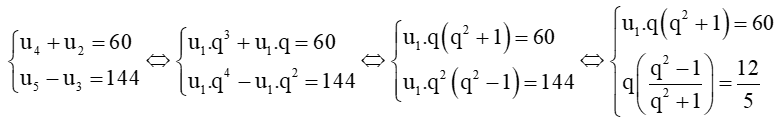Toán 11 Chân trời sáng tạo): Bài tập cuối chương 2
Với giải bài tập Toán lớp 11 Bài tập cuối chương 2 sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 11.
Giải Toán 11 Bài tập cuối chương 2
Bài tập
Lời giải:
Đáp án đúng là: B
Dãy số (un) có ba số hạng đầu tiên là:
;
;
Bài 2 trang 61 Toán 11 Tập 1: Cho dãy số . Số hạng tổng quát của dãy số này là:
Lời giải:
Đáp án đúng là: C
Dãy số lập thành một cấp số nhân có số hạng đầu là và công bội q = , có số hạng tổng quát là: .
Bài 3 trang 61 Toán 11 Tập 1: Cho dãy số (un) với . Phát biểu nào sau đây là đúng?
C. Dãy số giảm và bị chặn dưới;
D. Dãy số giảm và bị chặn trên.
Lời giải:
Đáp án đúng là: A
+) Ta có:
Xét hiệu
Vì n ∈ ℕ* nên n > 0, suy ra .
Do đó un+1 > un hay (un) là dãy tăng.
+) Ta có:
Vì n ∈ ℕ* nên n ≥ 1 suy ra n + 2 ≥ 3
.
Ta lại có n ∈ ℕ* nên n > 0 suy ra . Do đó .
Vì vậy nên dãy số (un) bị chặn.
Lời giải:
Đáp án đúng là: D
Cấp số cộng (un) có số hạng đầu u1, công sai d có số hạng tổng quát là:
un = u1 + (n – 1)d, với n ≥ 2.
Bài 5 trang 61 Toán 11 Tập 1: Cho cấp số cộng (un) có u1 = 3 và u2 = – 1. Khi đó
Lời giải:
Đáp án đúng là: C
Ta có: u2 = u1 + d = – 1
⇔ d = – 1 – u1 = – 1 – 3 = – 4.
Khi đó u3 = u1 + 2d = 3 + 2(– 4) = – 5.
Lời giải:
Đáp án đúng là: D
Ta có: u5 = u1 + 4d = – 1 + 4.3 = 11.
Tổng năm số hạng đầu của cấp số cộng (un) có số hạng đầu u1 = – 1 và công sai d = 3 là: .
Lời giải:
Đáp án đúng là: B
Để 2x – 1; x; 2x + 1 theo thứ tự lập thành cấp số nhân thì:
x2 = (2x – 1)(2x + 1)
⇔ x2 = 4x2 – 1
⇔ 3x2 = 1
⇔ 
Vì vậy có hai số thực số x thỏa mãn điều kiện bài toán.
Lời giải:
Đáp án đúng là: D
Giả sử tam giác có số đo các góc theo thứ tự tăng dần lần lượt: x; y; z (rad).
Vì x; y; z lập thành cấp số nhân có công bội q = 2 nên ta có:
y = x.2 = 2x, z = 22.x = 4x.
Mặt khác ta có: x + y + z = π
⇔ x + 2x + 4x = π
⇔ 7x = π
⇔ x = .
⇒ y = và z = .
Bài 9 trang 62 Toán 11 Tập 1: Xét tính tăng, giảm của dãy số (un) với .
Lời giải:
+) Ta có:
Xét
Suy ra
Vì vậy dãy số tăng.
+) Vì n ∈ ℕ* nên n ≥ 1 do đó 3n – 1 ≥ 2 > 0 và 2n > 0 nên .
Do đó dãy số bị chặn dưới.
Bài 10 trang 62 Toán 11 Tập 1: Xét tính bị chặn của dãy số (un) với .
Lời giải:
Ta có:
+) Vì n ∈ ℕ* nên n ≥ 1, suy ra n + 2 ≥ 3
+) Vì n ∈ ℕ* nên n > 0 suy ra
Do đó ta có: hay dãy số (un) bị chặn.
Bài 11 trang 62 Toán 11 Tập 1: Tìm số hạng đầu u1 và công sai d của cấp số cộng (un), biết:
Lời giải:
a) 
Vậy cấp số cộng (un) có số hạng đầu u1 = 8 và công sai d = – 3.
b) 
Vậy cấp số cộng (un) có số hạng đầu u1 = 30 và công sai d = 3 hoặc số hạng đầu u1 = 18 và công sai d = .
Bài 12 trang 62 Toán 11 Tập 1: Tìm số hạng đầu u1 và công bội q của cấp số nhân (un), biết:
Lời giải:
a) 
Vậy cấp số nhân (un) có số hạng đầu u1 = 6 và công bội q = 2.
b) 
Xét
⇔ 5(q3 – q) = 12(q2 + 1)
⇔ 5q3 – 12q2 – 5q – 12 = 0
⇔ (q – 3)(5q2 + 3q + 4) = 0
⇔ q = 3 (do 5q2 + 3q + 4 = 0 vô nghiệm)
⇒ u1 = 2.
Vậy cấp số nhân (un) có số hạng đầu u1 = 2 và công bội q = 3.
Lời giải:
Gọi số cá thể ở thời điểm ban đầu của một quần thể động vật là u1 = 110 000 (cá thể).
Sau 1 năm số cá thể của quần thể là: u1 + 12%u1 – 2%u1 – 8%u1 = u1 + 2%u1 (cá thể).
Sau 2 năm số cá thể của quần thể là: u1 + 2%u1 + 2%(u1 + 2%u1) = (1 + 2%).(u1 + 2%u1) = (1 + 2%)2.u1 = (1 + 2%)2.110 000 = 114 444(cá thể).
Lời giải:
Ta có tần số âm thanh các phím liên tiếp tạo thành một cấp số nhân (un).
Đặt tần số âm thanh của phím La Trung là số hạng đầu u1 = 400.
Phím La Cao cao hơn 12 phím so với phím La Trung nên phím này ở u13 = 800.
Ta lại có: u13 = u1.q12 = 400q12 = 800 ⇔ q = .
Vậy công bội của cấp số nhân trên là 1,059.
Lời giải:
Dân số Việt Nam qua mỗi năm lập thành một cấp số nhân có số hạng đầu u1 = 97,6 (triệu người), công bội q = 1 + 1,14% = 1,0114. Suy ra công thức số hạng tổng quát là: un = 97,6.(1,0114)n-1.
Từ năm 2020 đến năm 2040 có 21 năm nghĩa là dân số của Việt Nam năm 2040 là u22 =97,6.(1,0114)21 = 123,832 (triệu người).
Xem thêm lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Chân trời sáng tạo (hay nhất)
- Văn mẫu lớp 11 - Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn 11 – Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn lớp 11 - Chân trời sáng tạo
- Giải SBT Ngữ văn 11 – Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Ngữ văn 11 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Chân trời sáng tạo
- Soạn văn 11 Chân trời sáng tạo (ngắn nhất)
- Giải sgk Tiếng Anh 11 – Friends Global
- Giải sbt Tiếng Anh 11 - Friends Global
- Trọn bộ Từ vựng Tiếng Anh 11 Friends Global đầy đủ nhất
- Bài tập Tiếng Anh 11 Friends Global theo Unit có đáp án
- Giải sgk Vật lí 11 – Chân trời sáng tạo
- Lý thuyết Vật lí 11 – Chân trời sáng tạo
- Giải sbt Vật lí 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Vật lí 11 – Chân trời sáng tạo
- Giải sgk Hóa học 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Hóa học 11 – Chân trời sáng tạo
- Lý thuyết Hóa 11 - Chân trời sáng tạo
- Giải sbt Hóa học 11 – Chân trời sáng tạo
- Giải sgk Sinh học 11 – Chân trời sáng tạo
- Lý thuyết Sinh học 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Sinh học 11 – Chân trời sáng tạo
- Giải sbt Sinh học 11 – Chân trời sáng tạo
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Chân trời sáng tạo
- Lý thuyết Kinh tế pháp luật 11 – Chân trời sáng tạo
- Giải sbt Kinh tế pháp luật 11 – Chân trời sáng tạo
- Giải sgk Lịch sử 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Lịch sử 11 – Chân trời sáng tạo
- Lý thuyết Lịch sử 11 - Chân trời sáng tạo
- Giải sbt Lịch sử 11 – Chân trời sáng tạo
- Giải sgk Địa lí 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Địa lí 11 – Chân trời sáng tạo
- Lý thuyết Địa lí 11 - Chân trời sáng tạo
- Giải sbt Địa lí 11 – Chân trời sáng tạo
- Giải sgk Hoạt động trải nghiệm 11 – Chân trời sáng tạo