Toán 11 Bài 1 (Chân trời sáng tạo): Tìm hiểu hàm số lượng giác bằng phần mềm GeoGebra
Với giải bài tập Toán lớp 11 Bài 1: Tìm hiểu hàm số lượng giác bằng phần mềm GeoGebra sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 11 Bài 1.
Giải Toán 11 Bài 1: Tìm hiểu hàm số lượng giác bằng phần mềm GeoGebra
Chuẩn bị:
- Máy tính xách tay có cài đặt phần mềm GeoGebra hoặc có kết nối Internet.
- Máy chiếu hoặc màn hình ti vi lớn.
- Thực hành trong phòng máy nếu các trường có điều kiện.
- Sách giáo khoa Toán 11, tập một – bộ sách Chân trời sáng tạo.
Hướng dẫn chức năng của GeoGebra
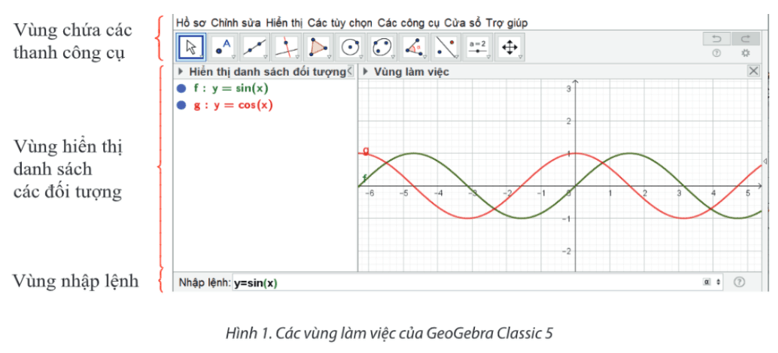
Để vẽ đồ thị trên GeoGebra ta thực hiện các thao tác trên bốn vùng sau:
1. Vùng chứa các thanh công cụ;
2. Vùng hiển thị danh sách các đối tượng;
3. Vùng làm việc: chứa đồ thị vẽ được của các hàm số lượng giác;
4. Vùng nhập lệnh: để nhập công thức các hàm số và biểu thức.
Tổ chức hoạt động
Chia lớp thành các nhóm, mỗi nhóm từ 4 đến 8 học sinh.
Nhóm trưởng phân công các thành viên trong nhóm thực hiện các hoạt động sau:
Hoạt động 1 trang 146 Toán 11 Tập 1: Vẽ đồ thị hàm số y = sin x
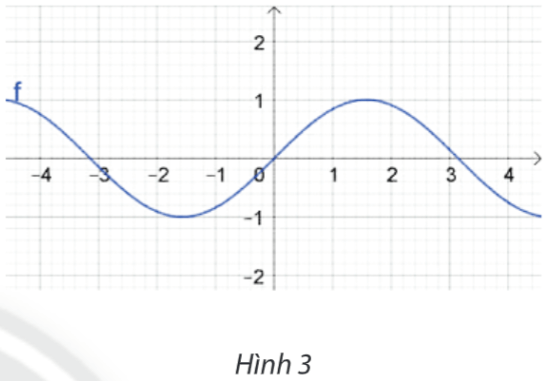
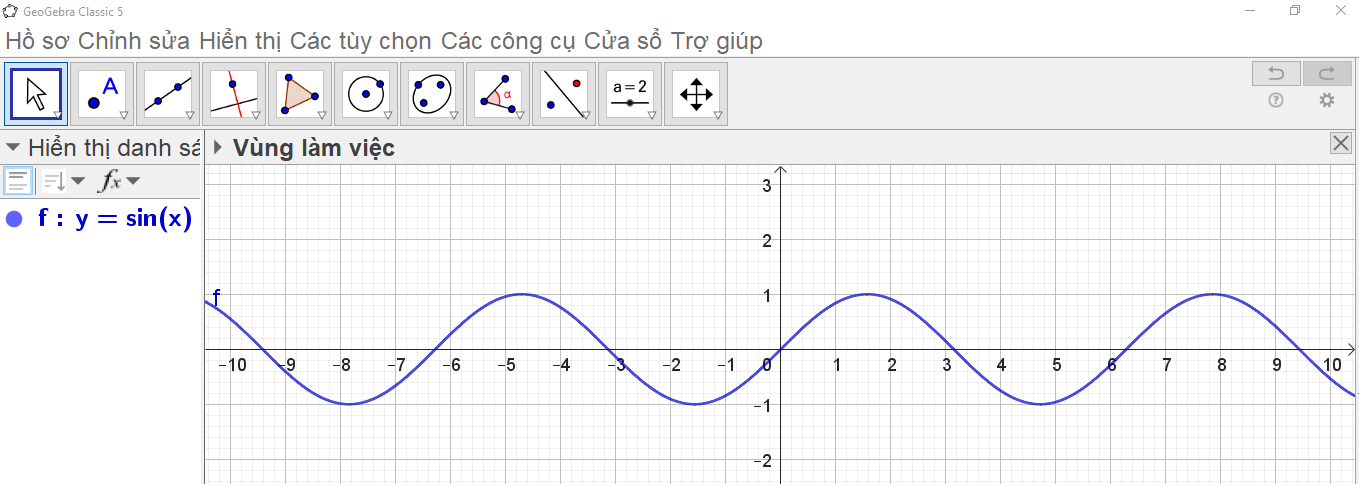
3. Ta có ngay đồ thị hàm số y = sin x trên vùng làm việc như Hình 3.
Lời giải:
Học sinh thực hiện theo các bước ở hoạt động 1.
Lời giải:
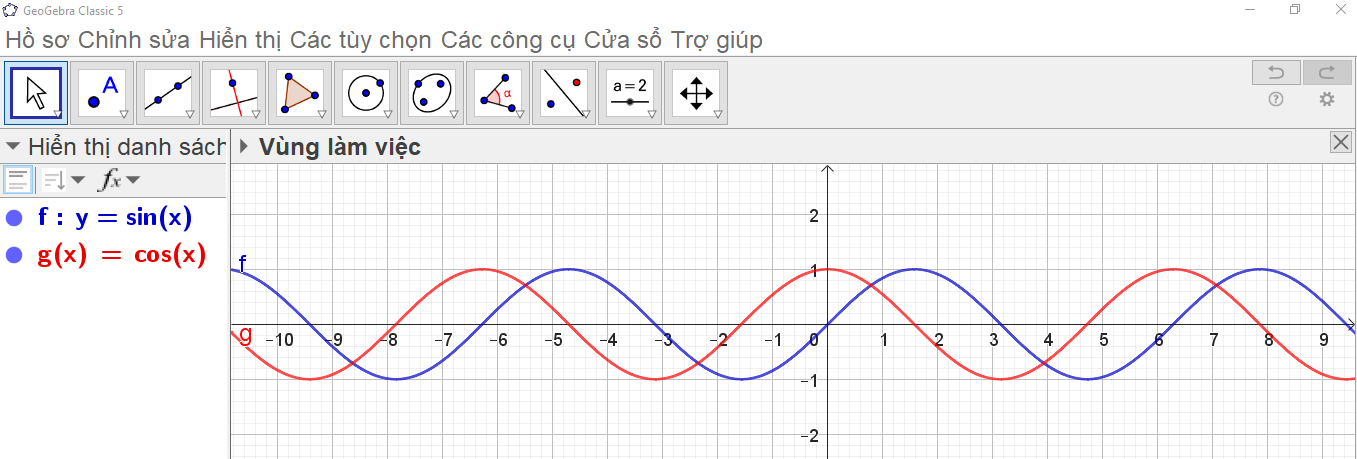
• Ta đã vẽ hàm số y = sin x trên hệ trục tọa độ ở hoạt động 1 (như hình vẽ).
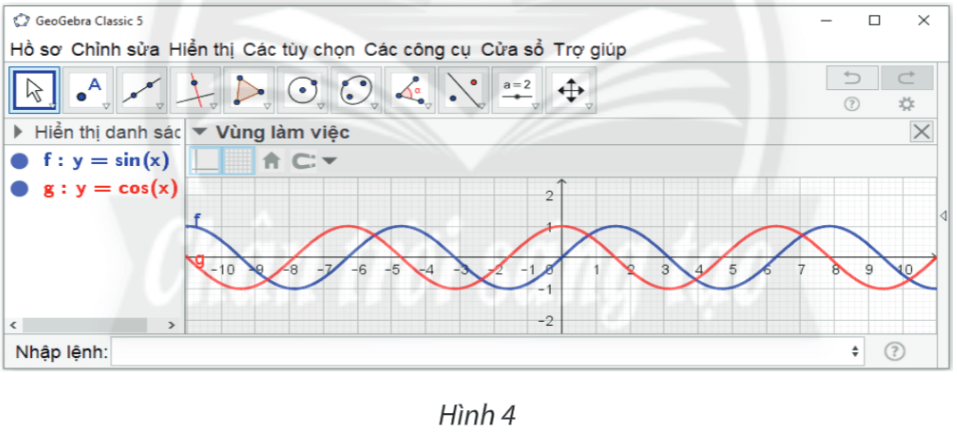
• Thao tác trên Geogebra: Nhập phương trình theo cú pháp y = cos(x) vào vùng nhập lệnh.
• Ta có ngay đồ thị hàm số y = cos x trên vùng làm việc như hình vẽ.
Lời giải:
Ta thực hiện vẽ đồ thị hàm số lượng giác y = tan x và y = cot x trên cùng hệ trục tọa độ theo các bước sau:
Bước 1. Khởi động phần mềm đã cài đặt trên máy tính hoặc truy cập vào trang web: https://www.geogebra.org/ để sử dụng phiên bản online.
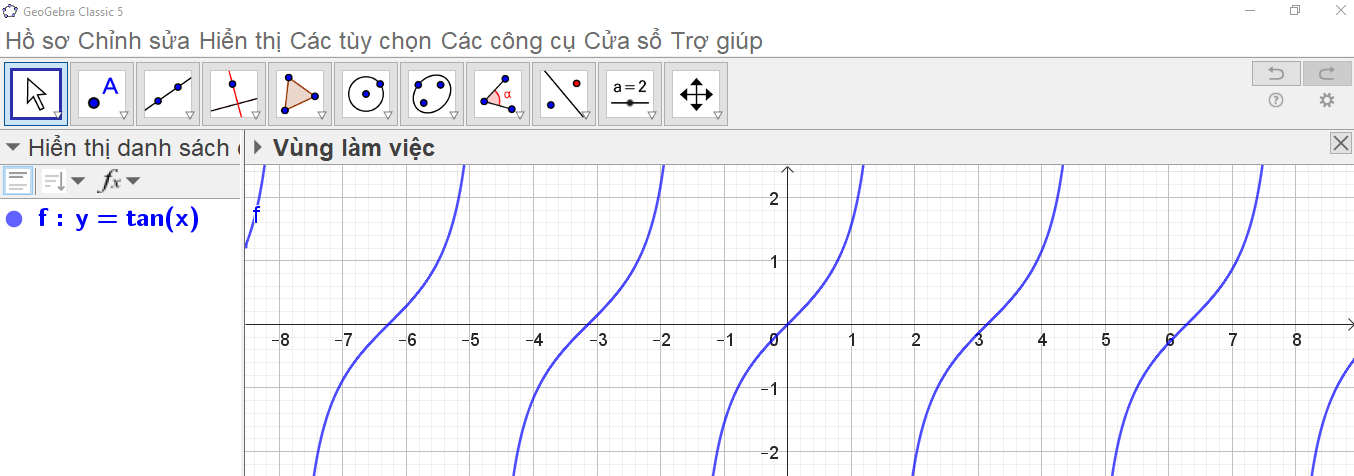
Bước 2. Các bước thao tác trên Geogebra: Nhập phương trình theo cú pháp y = tan(x) vào vùng nhập lệnh (như hình vẽ).
Ta có ngay đồ thị hàm số y = tan x trên vùng làm việc như hình vẽ.
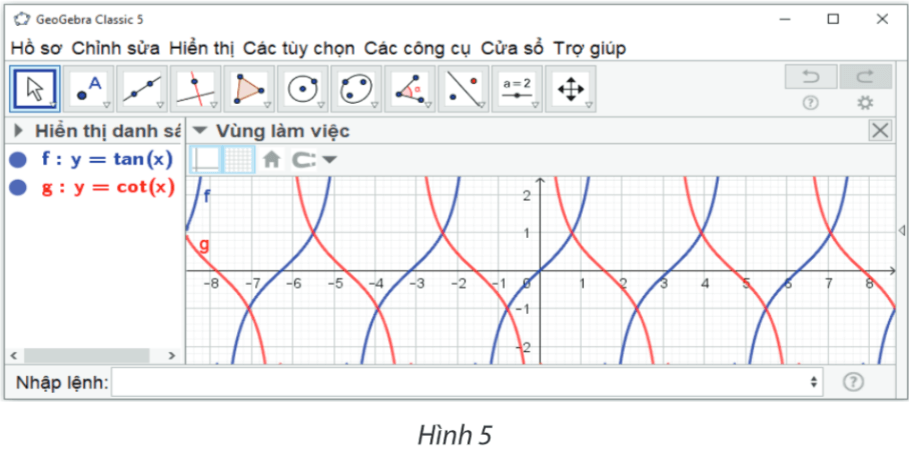
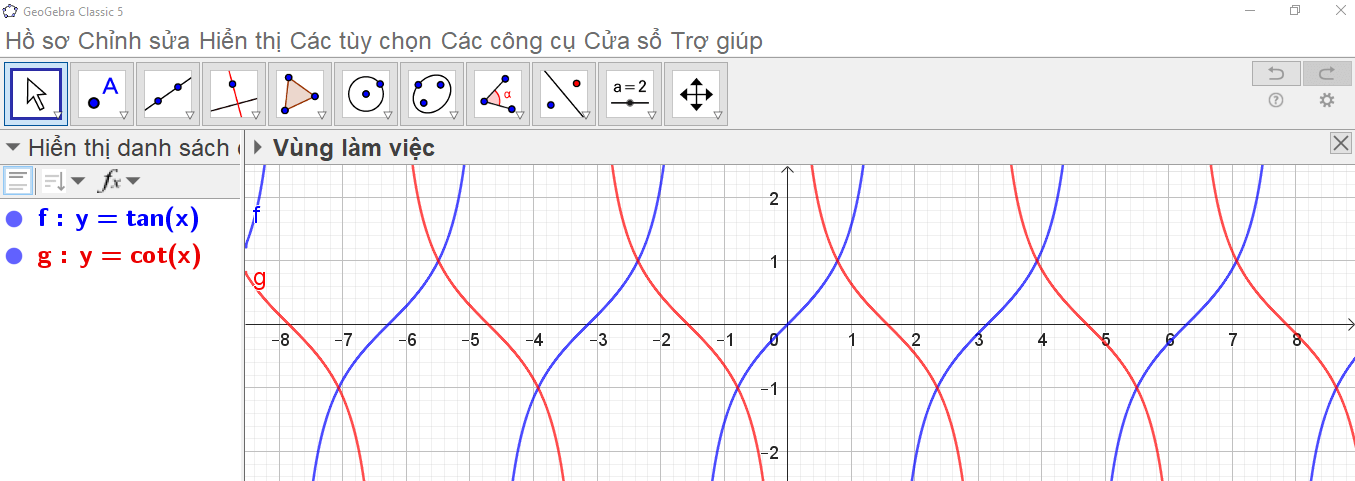
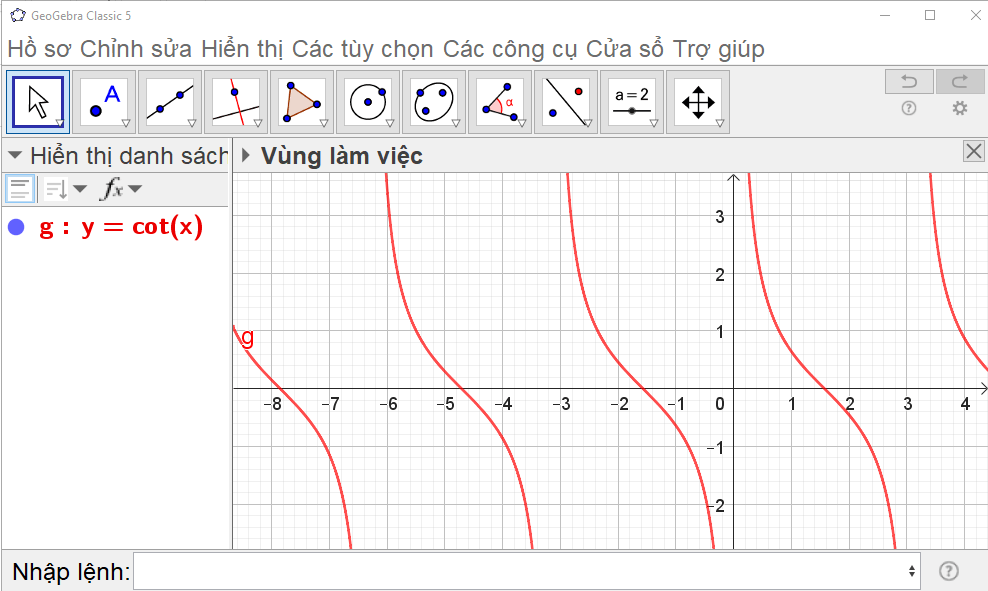
Bước 3. Các bước thao tác trên Geogebra: Nhập phương trình theo cú pháp y = cot(x) vào vùng nhập lệnh (như hình vẽ).
Ta có ngay đồ thị hàm số y = cot x trên vùng làm việc như hình vẽ.
Hoạt động 2 trang 147 Toán 11 Tập 1: Dùng đồ thị để giải thích tính chất của các hàm số lượng giác
Lời giải:
Ví dụ.
Lời giải:
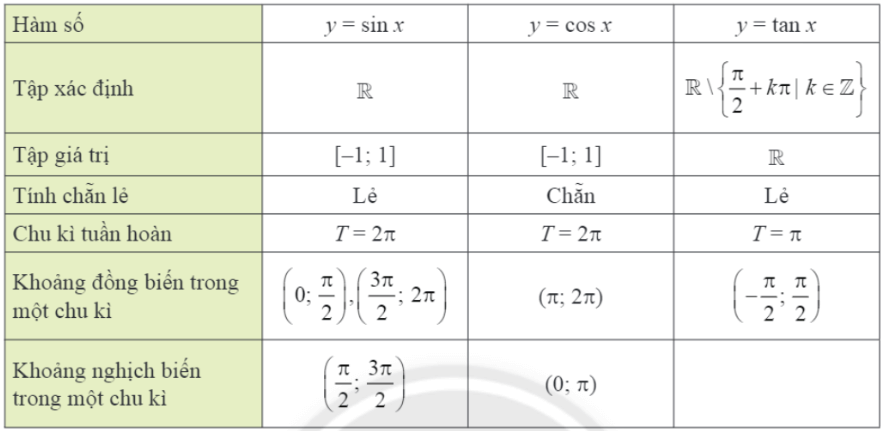
Dựa vào đồ thị hàm số y = cot x, ta có:
• Tập xác định: D = ℝ\{kπ | k ∈ ℤ}.
• Tập giá trị: ℝ.
• Tính chẵn lẻ: hàm số y = cot x là hàm số lẻ.
• Tính tuần hoàn: hàm số y = cot x là hàm tuần hoàn.
• Chu kì: T = π.
• Hàm số y = cot x không có khoảng đồng biến.
• Hàm số y = cot x nghịch biến trên (kπ; π + kπ) (k ∈ ℤ).
Xem thêm lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Số trung bình và mốt của mẫu số liệu ghép nhóm
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Chân trời sáng tạo (hay nhất)
- Văn mẫu lớp 11 - Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn 11 – Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn lớp 11 - Chân trời sáng tạo
- Giải SBT Ngữ văn 11 – Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Ngữ văn 11 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Chân trời sáng tạo
- Soạn văn 11 Chân trời sáng tạo (ngắn nhất)
- Giải sgk Tiếng Anh 11 – Friends Global
- Giải sbt Tiếng Anh 11 - Friends Global
- Trọn bộ Từ vựng Tiếng Anh 11 Friends Global đầy đủ nhất
- Bài tập Tiếng Anh 11 Friends Global theo Unit có đáp án
- Giải sgk Vật lí 11 – Chân trời sáng tạo
- Lý thuyết Vật lí 11 – Chân trời sáng tạo
- Giải sbt Vật lí 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Vật lí 11 – Chân trời sáng tạo
- Giải sgk Hóa học 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Hóa học 11 – Chân trời sáng tạo
- Lý thuyết Hóa 11 - Chân trời sáng tạo
- Giải sbt Hóa học 11 – Chân trời sáng tạo
- Giải sgk Sinh học 11 – Chân trời sáng tạo
- Lý thuyết Sinh học 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Sinh học 11 – Chân trời sáng tạo
- Giải sbt Sinh học 11 – Chân trời sáng tạo
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Chân trời sáng tạo
- Lý thuyết Kinh tế pháp luật 11 – Chân trời sáng tạo
- Giải sbt Kinh tế pháp luật 11 – Chân trời sáng tạo
- Giải sgk Lịch sử 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Lịch sử 11 – Chân trời sáng tạo
- Lý thuyết Lịch sử 11 - Chân trời sáng tạo
- Giải sbt Lịch sử 11 – Chân trời sáng tạo
- Giải sgk Địa lí 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Địa lí 11 – Chân trời sáng tạo
- Lý thuyết Địa lí 11 - Chân trời sáng tạo
- Giải sbt Địa lí 11 – Chân trời sáng tạo
- Giải sgk Hoạt động trải nghiệm 11 – Chân trời sáng tạo