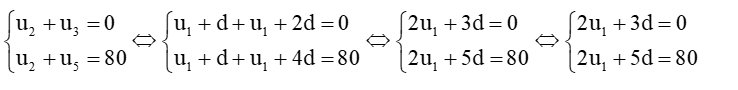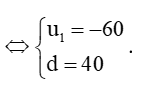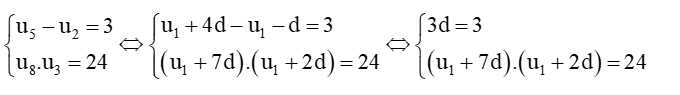Toán 11 Bài 2 (Chân trời sáng tạo): Cấp số cộng
Với giải bài tập Toán lớp 11 Bài 2: Cấp số cộng sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 11 Bài 2.
Giải bài tập Toán 11 Bài 2: Cấp số cộng
Bài giảng Toán 11 Bài 2: Cấp số cộng
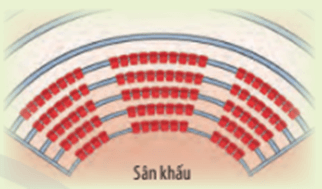
Bạn hãy đếm và nêu nhận xét về số ghế của năm hàng đầu tiên.
Làm thế nào để biết được số ghế của một hàng bất kì và tính được tổng số ghế trong rạp hát đó?
Lời giải:
Tiến hành đếm, ta có được kết quả sau:
Hàng 1: có 14 ghế;
Hàng 2: có 17 ghế;
Hàng 3: có 20 ghế;
Hàng 4: có 23 ghế;
Hàng 5: có 26 ghế.
Dựa vào số ghế của 5 hàng ghế đầu ta thấy hàng sau hơn hàng trước 3 ghế.
Sau bài học này ta biết số ghế của mỗi hàng ghế lập thành một cấp số cộng, có công thức tổng quát là: un = u1 + (n – 1)d; trong đó u1 = 14 là số ghế của hàng đầu tiên, d = 3 là công sai.
1. Cấp số cộng
Hoạt động khám phá 1 trang 52 Toán 11 Tập 1: Tìm điểm giống nhau của các dãy số sau:
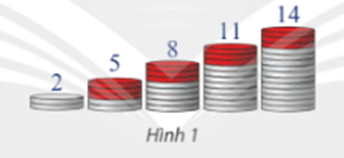
a) 2; 5; 8; 11; 14 (xem Hình 1).
Lời giải:
Nhận xét: Điểm giống nhau của các dãy số là:
Dãy số trên đều là các dãy số tăng.
Kể từ số hạng thứ hai, mỗi số hạng đều bằng tổng của số hạng đứng ngay trước nó với một số d không đổi.
b) Dãy số (un) với un = 9n – 9.
c) Dãy số (vn) với vn = an + b, trong đó a và b là các hằng số.
Lời giải:
a) Dãy số 3; 7; 11; 15; 19; 23 là cấp số cộng với công sai d = 4.
b) Ta có: u1 = 9.1 – 9 = 0.
un+1 = 9(n + 1) – 9 = 9n – 9 + 9 = un + 9, ∀n ∈ ℕ*.
Vậy dãy số (un) là cấp số cộng với số hạng đầu u1 = 0 và công sai d = – 3.
c) Ta có: v1 = a.1 + b = a + b.
vn+1 = a(n + 1) + b = an + a + b = an + b + a = vn + a, ∀n ∈ ℕ*.
Vậy dãy số (vn) là cấp số cộng với số hạng đầu v1 = a + b và công sai là d = a.
Lời giải:
Giả sử tam giác vuông thỏa mãn điều kiện bài toán là tam giác ABC vuông tại A.
Đặt ˆB=α,ˆC=β,ˆA=90°(α<β<90°)ˆB=α,ˆC=β,ˆA=90°(α<β<90°).
Ta có: α, β, 90° là một cấp số cộng nên ta có: β=α+90°2β=α+90°2
Mặt khác, ta có: α + β + 90° = 180°
⇔α+α+90°2+90°=180°⇔α+α+90°2+90°=180°
⇔3α=90°⇔3α=90°
⇔α=30°⇔α=30°
⇒β=30°+90°2=60°⇒β=30°+90°2=60°.
Vậy ˆB=30°,ˆC=60°,ˆA=90°ˆB=30°,ˆC=60°,ˆA=90°.
Lời giải:
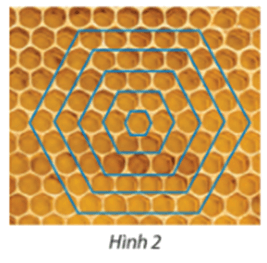
Vòng 1: Có 6 ô;
Vòng 2: Có 12 ô;
Vòng 3: Có 18 ô;
...
Ta có dãy số: 6; 12; 18; ...
Từ số hạng thứ 2 trở đi số hạng sau hơn số hạng trước 6 đơn vị nên đây là một cấp số cộng có số hạng đầu là 6 và công sai là 6.
2. Số hạng tổng quát của cấp số cộng
Lời giải:
Ta có:
u2 – u1 = d;
u3 – u1 = 2d;
u4 – u1 = 3d;
...
un – u1 = (n – 1)d.
Thực hành 3 trang 54 Toán 11 Tập 1: Tìm số hạng tổng quát của các cấp số cộng sau:
a) Cấp số cộng (an) có a1 = 5 và d = – 5;
b) Cấp số cộng (bn) có b1 = 2 và b10 = 20.
Lời giải:
a) Cấp số cộng (an) có a1 = 5 và d = – 5
Số hạng tổng quát là:
an = a1 + (n – 1).d = 5 + (n – 1).(– 5) = 5 + – 5n + 5 = – 5n + 10.
b) Cấp số cộng (bn) có b1 = 2 và b10 = 20.
Số hạng tổng quát là: bn = b1 + (n – 1)d
Khi đó b10 = 2 + (10 – 1).d = 2 + 9d = 20
⇒ d = 2
Vậy số hạng tổng quát là: bn = 2 + (n – 1).2 = 2n.
Vận dụng 2 trang 54 Toán 11 Tập 1: Tìm số hạng tổng quát của cấp số cộng (cn) có c4 = 80 và c6 = 40.
Lời giải:
Ta có: c4 = c1 + 3d = 80 và c6 = c1 + 5d = 40. Khi đó ta có hệ phương trình:
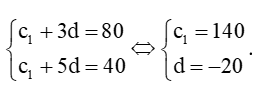
Khi đó số hạng tổng quát của cấp số cộng trên là:
cn = 140 + (n – 1).(– 20) = – 20n +160.
Vậy số hạng tổng quát của cấp số cộng (cn) là: cn = – 20n + 160.
3. Tổng của n số hạng đầu tiên của cấp số cộng
Hoạt động khám phá 3 trang 54 Toán 11 Tập 1: Cho cấp số cộng (un) có công sai d.
a) Tính các tổng un + u1; u2 + un-1; u3 + un-2; ...; uk + un-k+1 theo u1, n và d.
b) Chứng tỏ rằng 2(u1 + u2 + u3 + ... + un) = n(u1 + un).
Lời giải:
a) Ta có: un = u1 + (n – 1)d, un-1 = u1 + (n – 1 – 1)d = u1 + (n – 2)d
Khi đó:
u1 + un = u1 + u1 + (n – 1)d = 2u1 + (n – 1)d;
u2 + un-1 = u1 + d + u1 + (n – 2)d = 2u1 + (n – 1)d;
u3 + un-2 = u1 + 2d + u1 + (n – 3)d = 2u1 + (n – 1)d;
...
uk + un-k+1 = u1 + (k – 1)d + u1 + (n – k + 1 – 1)d = 2u1 + (n – 1)d;
Vậy u1 + un = u2 + un-1 = u3 + un-2 = ... = uk + un-k+1.
b) Ta có: 2(u1 + u2 + u3 + ... + un)
= 2[(u1 + un) + (u2 + un-1) + (u3 + un-2) + ... + (uk + un-k+1)]
= 2[(u1 + un) + (u1 + un) + ... + (u1 + un)]
= 2.n2(u1+un)2.n2(u1+un) = n(u1 + un) .
Thực hành 4 trang 55 Toán 11 Tập 1:
a) Tính tổng 50 số tự nhiên chẵn đầu tiên.
b) Cho cấp số cộng (un) có u3 + u28 = 100. Tính tổng 30 số hạng đầu tiên của cấp số cộng đó.
c) Cho cấp số cộng (vn) có S6 = 110. Tính S20.
Lời giải:
a) 50 số tự nhiên chẵn lập thành một cấp số cộng, có u1 = 0, công sai d = 2.
Khi đó tổng của 50 số này là:
S50=50(0+50)2=1250S50=50(0+50)2=1250.
b) Ta có: u3 + u28 = u1 + 2d + u1 + 27d = 2u1 + 29d = 100
Tổng của 30 số hạng đầu tiên của cấp số cộng đó là:
S30=30(u1+u30)2=30.(u1+u1+29d)2=30(2u1+29d)2=30.1002=1500.
c) Ta có:
S6=6(u1+u6)2=6.(u1+u1+5d)2=6(2u1+5d)2=18⇔2u1+5d=6
Tổng của 10 số hạng đầu tiên của cấp số cộng đó là:
S10=10(u1+u10)2=10.(u1+u1+9d)2=10(2u1+9d)2=110⇔2u1+9d=22
Khi đó ta có hệ phương trình: 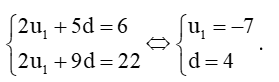
Tổng 20 số hạng đầu tiên của cấp số cộng là:
S10=10(u1+u10)2=10.(u1+u1+9d)2=10(2u1+9d)2=110⇔2u1+9d=22
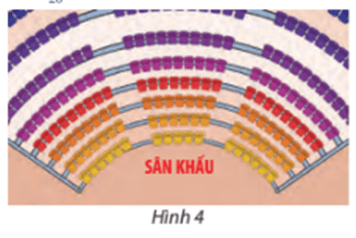
Lời giải:
Số ghế của mỗi hàng lập thành một cấp số cộng, có số hạng đầu là u1 = 7, công sai d = 3. Khi đó số hạng tổng quát của cấp số cộng là: un = u1 + (n – 1)d = 7 + (n – 1).3.
a) Số ghế có ở hàng cuối cùng (hàng số 20) là: u20 = 17 + (20 – 1).3 = 74.
b) Tổng số ghế có trong rạp là tổng của 20 số hạng đầu trong cấp số cộng và bằng:
S20=20(17+74)2=910.
Vậy tổng số ghế trong rạp là 910 ghế.
Bài tập
Bài 1 trang 56 Toán 11 Tập 1: Chứng minh dãy số hữu hạn sau là cấp số cộng: 1; – 3; – 7; – 11; – 15.
Lời giải:
Dãy số 1; – 3; – 7; – 11; – 15 có số hạng đầu là u1 = 1, từ số hạng thứ hai trở đi ta thấy số hạng sau hơn số hạng trước – 4 đơn vị nên đây là một cấp số cộng có công sai d = – 4.
Lời giải:
Công thức số hạng tổng quát của dãy số (un) có số hạng đầu u1 = 4 và công sai d = – 10 là:
un = 4 + (n – 1).10 = 10n – 6.
Bài 3 trang 56 Toán 11 Tập 1: Cho cấp số cộng (un) có số hạng đầu u1 = – 3 và công sai d = 2.
b) Số 195 là số hạng thứ bao nhiêu của cấp số cộng đó?
Lời giải:
Số hạng tổng quát của cấp số cộng (un) với số hạng đầu u1 = – 3 và công sai d = 2 là:
un = – 3 + (n – 1).2 = 2n – 5.
a) Ta có u12 = 2.12 – 5 = 19.
b) Xét un = 195
⇔ 2n – 5 = 195
⇔ n = 100
Vậy số 195 là số hạng thứ 100 của cấp số cộng.
Lời giải:
a) Ta có:
u1 = 3 – 4.1 = – 1;
un+1 = 3 – 4(n + 1) = 3 – 4n – 4 = un – 4, ∀n ∈ ℕ*.
Vậy (un) là một cấp số cộng có số hạng đầu là – 1 và công sai d = – 4.
b) Ta có:
u1 = 12−4=−72;
un+1 = n+12−4=n2−4+12=un+12,∀n∈ℕ*.
Vậy (un) là một cấp số cộng có số hạng đầu là −72 và công sai d=12.
c) Dãy số (un) không phải cấp số cộng vì:
u1 = 51 = 5; u2 = 52 = 25; u2 = 53 = 125 và u2≠12(u1+u3).
d) Ta có:
u1 = 9−5.13=43
un+1 = 9−5(n+1)3=9−5n−53=9−5n3−53=un−53,∀n∈ℕ*.
Vậy (un) là một cấp số cộng có số hạng đầu là 43 và công sai d=−53.
Bài 5 trang 56 Toán 11 Tập 1: Tìm số hạng đầu và công sai của cấp số cộng (un), biết:
Lời giải:
a) 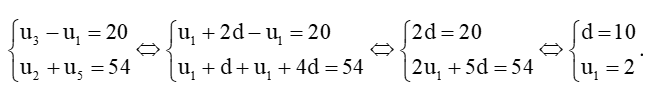
Vậy cấp số cộng (un) có số hạng đầu u1 = 2 và công sai d = 10.
b)
Vậy cấp số cộng (un) có số hạng đầu u1 = – 60 và công sai d = 40.
c)
⇔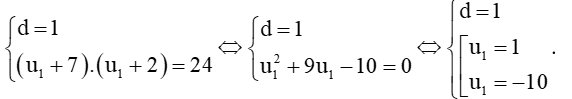
Vậy cấp số cộng (un) có số hạng đầu u1 = 1 và công sai d = 1 hoặc số hạng đầu u1 = – 10 và công sai d = 1.
a) Cái thang đó có bao nhiêu bậc?
Lời giải:
a) Dãy số 45; 43; 41; ...; 31 là một cấp số cộng có số hạng đầu u1 = 45 và công sai d = 2. Khi đó số hạng tổng quát của cấp số cộng trên là:
un = 45 + (n – 1)(– 2) = 47 – 2n, ∀n ∈ ℕ*.
Thanh cuối cùng có độ dài là 31 cm nên để tìm thang có bao nhiêu bậc tương ứng với tìm thanh ngang cuối cùng là số hạng thứ bao nhiêu trong cấp số cộng trên.
Ta có un = 47 – 2n = 31
⇔ n = 8
Vậy cái thang có 8 bậc.
b) Chiều dài thanh gỗ cần mua là tổng của 8 số hạng đầu tiên của cấp số cộng và bằng S8=8(45+31)2=304(cm).
a) Tính công sai của cấp số cộng trên.
b) Tính tổng chiều dài quãng đường rơi tự do của người đó trong 10 giây đầu tiên.
Lời giải:
a) Các quãng đường tạo thành cấp số cộng có công sai d = 48 – 16 = 32.
b) Cấp số cộng có số hạng đầu tiên là u1 = 16 và công sai d = 32, khi đó công thức số hạng tổng quát là: un = 16 + (n – 1).32 = 32n – 16.
Sau 10 giây buông dù quãng đường người đó rơi tự do là:
u10 = 32.10 – 16 = 304 (feet).
Tổng chiều dài quãng đường rơi tự do của người đó trong 10 giây đầu tiên cũng chính là tổng của 10 số hạng đầu tiên trong cấp số cộng và bằng:
S10=10(16+304)2=1600.
Vậy tổng chiều dài quãng đường rơi tự do của người đó trong 10 giây đầu tiên là 1 600 feet.
Lời giải:
Chiều cao của các cây lập thành một cấp số cộng un
Cây thấp nhất có kiểu gene aabb nên u1 = 100.
Nếu cứ thêm một alen trội A hay B thì chiều cao cây tăng thêm 5 cm do đó công sai của cấp số cộng là d = 5.
Vậy cây cao nhất với kiểu gene AABB có chiều cao là 100 + 5.4 = 120 (cm).
Lý thuyết Cấp số cộng
1. Cấp số cộng
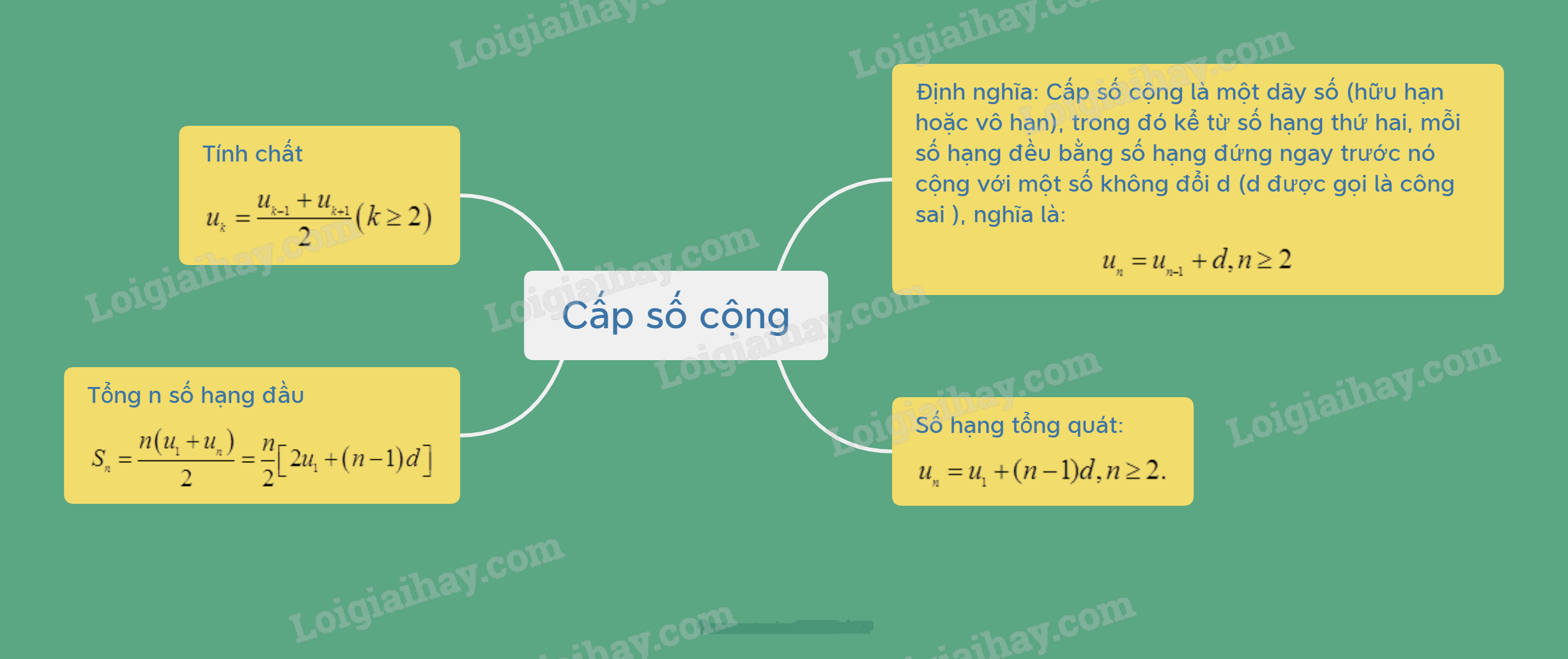
Cấp số cộng là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi d, nghĩa là:
un=un−1+d,n≥2
Số d được gọi là công sai của cấp số cộng.
* Nhận xét: Nếu (un) là cấp số cộng thì kể từ số hạng thứ 2, mỗi số hạng (trừ số hạng cuối đối với cấp số cộng hữu hạn) đều là trung bình cộng của 2 sô hạng đứng kề nó trong dãy, tức là:
uk=uk−1+uk+12(k≥2)
2. Số hạng tổng quát
Nếu cấp số cộng (un) có số hạng đầu là u1 và công sai d thì số hạng tổng quát uncủa nó được xác định theo công thứcun=u1+(n−1)d,n≥2.
3. Tổng n số hạng đầu của một cấp số cộng
Cho cấp số cộng (un)với công sai d. Đặt Sn=u1+u2+u3+...+un. Khi đó
Sn=n(u1+un)2=n2[2u1+(n−1)d]
Xem thêm lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Chân trời sáng tạo (hay nhất)
- Văn mẫu lớp 11 - Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn 11 – Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn lớp 11 - Chân trời sáng tạo
- Giải SBT Ngữ văn 11 – Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Ngữ văn 11 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Chân trời sáng tạo
- Soạn văn 11 Chân trời sáng tạo (ngắn nhất)
- Giải sgk Tiếng Anh 11 – Friends Global
- Giải sbt Tiếng Anh 11 - Friends Global
- Trọn bộ Từ vựng Tiếng Anh 11 Friends Global đầy đủ nhất
- Bài tập Tiếng Anh 11 Friends Global theo Unit có đáp án
- Giải sgk Vật lí 11 – Chân trời sáng tạo
- Lý thuyết Vật lí 11 – Chân trời sáng tạo
- Giải sbt Vật lí 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Vật lí 11 – Chân trời sáng tạo
- Giải sgk Hóa học 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Hóa học 11 – Chân trời sáng tạo
- Lý thuyết Hóa 11 - Chân trời sáng tạo
- Giải sbt Hóa học 11 – Chân trời sáng tạo
- Giải sgk Sinh học 11 – Chân trời sáng tạo
- Lý thuyết Sinh học 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Sinh học 11 – Chân trời sáng tạo
- Giải sbt Sinh học 11 – Chân trời sáng tạo
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Chân trời sáng tạo
- Lý thuyết Kinh tế pháp luật 11 – Chân trời sáng tạo
- Giải sbt Kinh tế pháp luật 11 – Chân trời sáng tạo
- Giải sgk Lịch sử 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Lịch sử 11 – Chân trời sáng tạo
- Lý thuyết Lịch sử 11 - Chân trời sáng tạo
- Giải sbt Lịch sử 11 – Chân trời sáng tạo
- Giải sgk Địa lí 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Địa lí 11 – Chân trời sáng tạo
- Lý thuyết Địa lí 11 - Chân trời sáng tạo
- Giải sbt Địa lí 11 – Chân trời sáng tạo
- Giải sgk Hoạt động trải nghiệm 11 – Chân trời sáng tạo


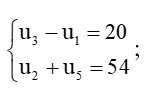 ;
;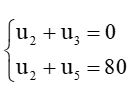 ;
;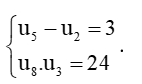 .
.