Giải Toán 11 trang 54 Tập 1 Chân trời sáng tạo
Với giải bài tập Toán 11 trang 54 trong Bài 2: Cấp số cộng sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 11 trang 54.
Giải Toán 11 trang 54 Tập 1
Lời giải:
Ta có:
u2 – u1 = d;
u3 – u1 = 2d;
u4 – u1 = 3d;
...
un – u1 = (n – 1)d.
Thực hành 3 trang 54 Toán 11 Tập 1: Tìm số hạng tổng quát của các cấp số cộng sau:
a) Cấp số cộng (an) có a1 = 5 và d = – 5;
b) Cấp số cộng (bn) có b1 = 2 và b10 = 20.
Lời giải:
a) Cấp số cộng (an) có a1 = 5 và d = – 5
Số hạng tổng quát là:
an = a1 + (n – 1).d = 5 + (n – 1).(– 5) = 5 + – 5n + 5 = – 5n + 10.
b) Cấp số cộng (bn) có b1 = 2 và b10 = 20.
Số hạng tổng quát là: bn = b1 + (n – 1)d
Khi đó b10 = 2 + (10 – 1).d = 2 + 9d = 20
⇒ d = 2
Vậy số hạng tổng quát là: bn = 2 + (n – 1).2 = 2n.
Vận dụng 2 trang 54 Toán 11 Tập 1: Tìm số hạng tổng quát của cấp số cộng (cn) có c4 = 80 và c6 = 40.
Lời giải:
Ta có: c4 = c1 + 3d = 80 và c6 = c1 + 5d = 40. Khi đó ta có hệ phương trình:
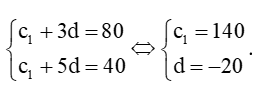
Khi đó số hạng tổng quát của cấp số cộng trên là:
cn = 140 + (n – 1).(– 20) = – 20n +160.
Vậy số hạng tổng quát của cấp số cộng (cn) là: cn = – 20n + 160.
3. Tổng của n số hạng đầu tiên của cấp số cộng
Hoạt động khám phá 3 trang 54 Toán 11 Tập 1: Cho cấp số cộng (un) có công sai d.
a) Tính các tổng un + u1; u2 + un-1; u3 + un-2; ...; uk + un-k+1 theo u1, n và d.
b) Chứng tỏ rằng 2(u1 + u2 + u3 + ... + un) = n(u1 + un).
Lời giải:
a) Ta có: un = u1 + (n – 1)d, un-1 = u1 + (n – 1 – 1)d = u1 + (n – 2)d
Khi đó:
u1 + un = u1 + u1 + (n – 1)d = 2u1 + (n – 1)d;
u2 + un-1 = u1 + d + u1 + (n – 2)d = 2u1 + (n – 1)d;
u3 + un-2 = u1 + 2d + u1 + (n – 3)d = 2u1 + (n – 1)d;
...
uk + un-k+1 = u1 + (k – 1)d + u1 + (n – k + 1 – 1)d = 2u1 + (n – 1)d;
Vậy u1 + un = u2 + un-1 = u3 + un-2 = ... = uk + un-k+1.
b) Ta có: 2(u1 + u2 + u3 + ... + un)
= 2[(u1 + un) + (u2 + un-1) + (u3 + un-2) + ... + (uk + un-k+1)]
= 2[(u1 + un) + (u1 + un) + ... + (u1 + un)]
= = n(u1 + un) .
Xem thêm lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Xem thêm lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Hoạt động khám phá 1 trang 52 Toán 11 Tập 1: Tìm điểm giống nhau của các dãy số sau:
a) 2; 5; 8; 11; 14 (xem Hình 1)...
Thực hành 3 trang 54 Toán 11 Tập 1: Tìm số hạng tổng quát của các cấp số cộng sau: a) Cấp số cộng (an) có a1 = 5 và d = – 5;...
Hoạt động khám phá 3 trang 54 Toán 11 Tập 1: Cho cấp số cộng (un) có công sai d. a) Tính các tổng un + u1; u2 + un-1; u3 + un-2; ...; uk + un-k+1 theo u1, n và d...
Thực hành 4 trang 55 Toán 11 Tập 1: a) Tính tổng 50 số tự nhiên chẵn đầu tiên. b) Cho cấp số cộng (un) có u3 + u28 = 100. Tính tổng 30 số hạng đầu tiên của cấp số cộng đó...
Bài 3 trang 56 Toán 11 Tập 1: Cho cấp số cộng (un) có số hạng đầu u1 = – 3 và công sai d = 2.
a) Tìm u12;...
Bài 5 trang 56 Toán 11 Tập 1: Tìm số hạng đầu và công sai của cấp số cộng (un)...
Xem thêm lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Chân trời sáng tạo (hay nhất)
- Văn mẫu lớp 11 - Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn 11 – Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn lớp 11 - Chân trời sáng tạo
- Giải SBT Ngữ văn 11 – Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Ngữ văn 11 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Chân trời sáng tạo
- Soạn văn 11 Chân trời sáng tạo (ngắn nhất)
- Giải sgk Tiếng Anh 11 – Friends Global
- Giải sbt Tiếng Anh 11 - Friends Global
- Trọn bộ Từ vựng Tiếng Anh 11 Friends Global đầy đủ nhất
- Bài tập Tiếng Anh 11 Friends Global theo Unit có đáp án
- Giải sgk Vật lí 11 – Chân trời sáng tạo
- Lý thuyết Vật lí 11 – Chân trời sáng tạo
- Giải sbt Vật lí 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Vật lí 11 – Chân trời sáng tạo
- Giải sgk Hóa học 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Hóa học 11 – Chân trời sáng tạo
- Lý thuyết Hóa 11 - Chân trời sáng tạo
- Giải sbt Hóa học 11 – Chân trời sáng tạo
- Giải sgk Sinh học 11 – Chân trời sáng tạo
- Lý thuyết Sinh học 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Sinh học 11 – Chân trời sáng tạo
- Giải sbt Sinh học 11 – Chân trời sáng tạo
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Chân trời sáng tạo
- Lý thuyết Kinh tế pháp luật 11 – Chân trời sáng tạo
- Giải sbt Kinh tế pháp luật 11 – Chân trời sáng tạo
- Giải sgk Lịch sử 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Lịch sử 11 – Chân trời sáng tạo
- Lý thuyết Lịch sử 11 - Chân trời sáng tạo
- Giải sbt Lịch sử 11 – Chân trời sáng tạo
- Giải sgk Địa lí 11 – Chân trời sáng tạo
- Giải Chuyên đề học tập Địa lí 11 – Chân trời sáng tạo
- Lý thuyết Địa lí 11 - Chân trời sáng tạo
- Giải sbt Địa lí 11 – Chân trời sáng tạo
- Giải sgk Hoạt động trải nghiệm 11 – Chân trời sáng tạo

