Giải Toán 11 trang 82 Tập 2 Chân trời sáng tạo

Giải Toán 11 trang 82 Tập 2

Bài 6 trang 82 Toán 11 Tập 2: Cho hình hộp đứng ABCD.A′B′C′D′ có cạnh bên AA′ = 2a và đáy ABCD là hình thoi có AB = a và $a\sqrt{3}$.

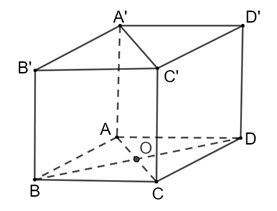
a) Tính khoảng cách giữa hai đường thẳng BD và AA′.

b) Tính thể tích của khối hộp.

Lời giải:

a) Vì hình hộp đứng $\mathrm{ABCD}.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ có đáy ABCD là hình thoi tâm O.

Do đó ta có: $\left\{\begin{array}{l}{\mathrm{AA}}^{\text{'}}\perp \left(\mathrm{ABCD}\right)\\ \mathrm{AC}\perp \mathrm{BD}\end{array}\right.\Rightarrow \left\{\begin{array}{l}{\mathrm{AA}}^{\text{'}}\perp \mathrm{OA}\\ \mathrm{OA}\perp \mathrm{BD}\end{array}\right.$

Suy ra là đoạn vuông góc chung của hai đường thẳng BD và AA^'.

Do đó $d\left(\mathrm{BD},{\mathrm{AA}}^{\text{'}}\right)=\mathrm{OA}=\frac{1}{2}\mathrm{AC}=\frac{a\sqrt{3}}{2}$

b) Đáy ABCD là hình thoi tâm O có AB = a và $\mathrm{AC}=a\sqrt{3}$

Do đó ta có: $\mathrm{BD}=2\mathrm{OB}=2\sqrt{{\mathrm{AB}}^2-{\mathrm{OA}}^2}=a$

Thể tích của khối hộp là:

$V={\mathrm{AA}}^{\text{'}}.S_{\mathrm{ABCD}}={\mathrm{AA}}^{\text{'}}.\frac{1}{2}\mathrm{AC}.\mathrm{BD}=\frac{1}{2}.2a.a\sqrt{3}.a=a^3\sqrt{3}.$

Vậy thể tích của khối hộp là ${\text{a}}^3\sqrt{3}.$

Bài 7 trang 82 Toán 11 Tập 2: Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a và có O là giao điểm hai đường chéo của đáy.

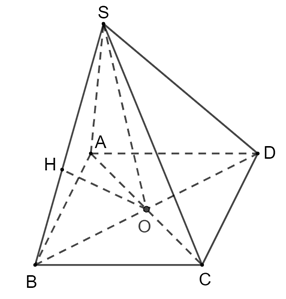
a) Tính khoảng cách giữa hai đường thẳng AC và SB.

b) Tính thể tích của khối chóp.

Lời giải:

a) Kẻ OH ⊥ SB (H $\in$SB)

S.ABCD là hình chóp tứ giác đều $\Rightarrow$ SO ⊥ (ABCD) $\Rightarrow$ SO ⊥AC.

Tứ giác ABCD là hình vuông suy ra AC ⊥ BD $\Rightarrow$ AC ⊥(SBD) $\Rightarrow$AC ⊥ OH.

Mà $\mathrm{OH}\perp \mathrm{SB}$

Do đó d(AC, SB) = OH

• Xét ΔABD vuông tại A, ta có:

$\mathrm{BD}=\sqrt{{\mathrm{AB}}^2+{\mathrm{AD}}^2}=a\sqrt{2}\Rightarrow \mathrm{BO}=\frac{1}{2}\mathrm{BD}=\frac{a\sqrt{2}}{2}$

• Xét ΔSBO vuông tại O, ta có:

$\mathrm{SO}=\sqrt{{\mathrm{SB}}^2-{\mathrm{BO}}^2}=\frac{a\sqrt{2}}{2}$

• Xét ΔSBO vuông tại O có SO = BO nên ΔSBO vuông cân tại O

Suy ra OH vừa là đường cao, vừa là đường trung tuyến.

Do đó $\mathrm{OH}=\frac{1}{2}\mathrm{SB}=\frac{a}{2}$

Vậy $\text{d}\left(\text{AC},\text{SB}\right)=\frac{a}{2}$

b) ${\text{S}}_{\mathrm{ABCD}}=a^2$ .

Thể tích khối chóp là: $V=\frac{1}{3}.\mathrm{SO}.S_{\mathrm{ABC}\text{D}}=\frac{a^3\sqrt{2}}{6}.$

Bài 8 trang 82 Toán 11 Tập 2: Tính thể tích của khối chóp cụt lục giác đều ABCDEF.A′B′C′D′E′F′ với O và O′ là tâm hai đáy, cạnh đáy lớn và đáy nhỏ lần lượt là a và $\frac{a}{2},{\mathrm{OO}}^{\text{'}}=a$.

Lời giải:

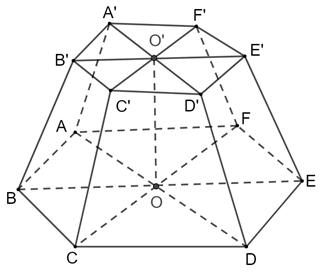
Ta có mỗi hình lục giác đều được tạo bởi 6 tam giác đều có cạnh bằng cạnh của hình lục giác.

Do đó ta có diện tích các đáy là:

$S=6.\frac{a^2\sqrt{3}}{4}=\frac{3\sqrt{3}{a}^2}{2},S^{\text{'}}=6.{\left(\frac{a}{2}\right)}^2\frac{\sqrt{3}}{4}=\frac{3\sqrt{3}{a}^2}{8}.$

Chiều cao của khối chóp cụt là: h = OO′ = a

Thể tích khối chóp cụt là:

$V=\frac{1}{3}h\left(S+\sqrt{S.S^{\text{'}}}+S\right)=\frac{1}{3}.a\left(\frac{3\sqrt{3}{a}^2}{2}+\frac{3\sqrt{3}{a}^2}{4}+\frac{3\sqrt{3}{a}^2}{8}\right)=\frac{7\sqrt{3}{a}^3}{8}.$

Vậy thể tích khối chóp cụt là $\frac{7\sqrt{3}{a}^3}{8}.$

Hoạt động khởi động trang 82 Toán 11 Tập 2: Mặt phẳng nghiêng thường được sử dụng trong lao động vì tính tiện dụng của nó. Quan sát hình mặt phẳng nghiêng (P) và mặt đất (Q) trong hình dưới đây và tìm hiểu tại sao:

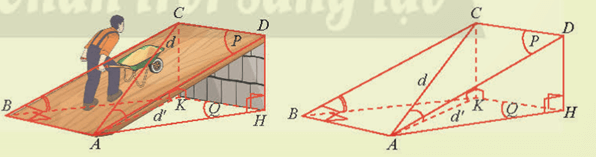
• $\widehat{\mathrm{CAK}}$ được gọi là góc hợp bởi đường thẳng d và (Q).

• $\widehat{\mathrm{CBK}}$ được gọi là góc hợp bởi hai mặt phẳng (P) và (Q).

Lời giải:

K là hình chiếu vuông góc của C lên (Q) nên $\widehat{\mathrm{CAK}}$ được gọi là góc hợp bởi đường thẳng d và (Q).

Ta có:

$\left.\begin{array}{l}\mathrm{CB}\perp \mathrm{AB}\\ \mathrm{BK}\perp \mathrm{AB}\\ \left(\mathrm{P}\right)\cap \left(\mathrm{Q}\right) \end{array}\right\}$

Nên $\widehat{\mathrm{CBK}}$ được gọi là góc hợp bởi hai mặt phẳng (P) và (Q)

1. Góc giữa đường thẳng và mặt phẳng

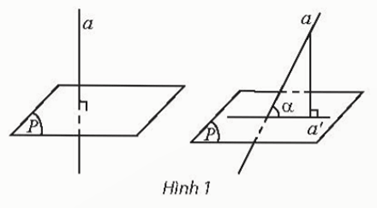
Hoạt động khám phá 1 trang 82 Toán 11 Tập 2: Cho đường thẳng a và mặt phẳng (P).

a) Trong trường hợp a vuông góc với (P), tìm góc giữa a và một đường thẳng b tuỳ ý trong (P).

b) Trong trường hợp a không vuông góc với (P), tìm góc giữa a và đường thẳng a′ là hình chiếu vuông góc của a trên (P).

Lời giải:

a) Ta có:

$\left.\begin{array}{c}\mathrm{a}\perp \left(\mathrm{P}\right)\\ \mathrm{b}\subset \left(\mathrm{P}\right)\end{array}\right\}\Rightarrow \text{a}\perp \text{b}\Rightarrow \left(\text{a},\text{b}\right)=90°$

b) Lấy A $\in$ a. Gọi $O=a\cap \left(P\right)$

Dựng AH ⊥ a′ (H$\in$ a′)

Ta có: $\left(a,a\text{'}\right)=\left(\mathrm{AO},\mathrm{OH}\right)=\widehat{\mathrm{AOH}}$

Xem thêm Lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Giải Toán 11 trang 74 Tập 2

Giải Toán 11 trang 75 Tập 2

Giải Toán 11 trang 76 Tập 2

Giải Toán 11 trang 77 Tập 2

Giải Toán 11 trang 78 Tập 2

Giải Toán 11 trang 79 Tập 2

Giải Toán 11 trang 81 Tập 2

Giải Toán 11 trang 82 Tập 2