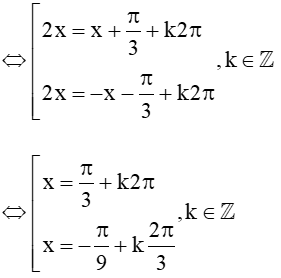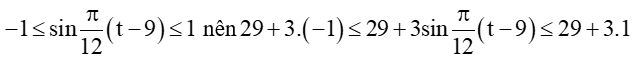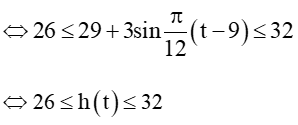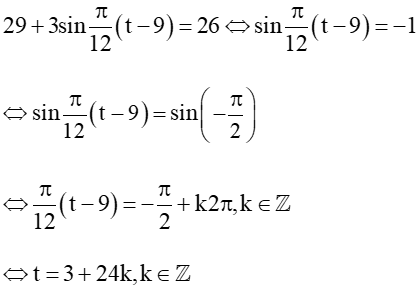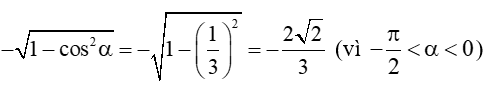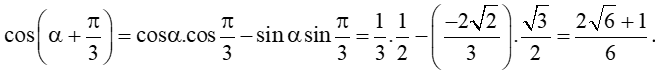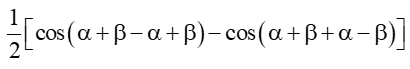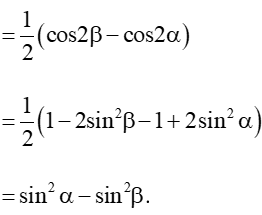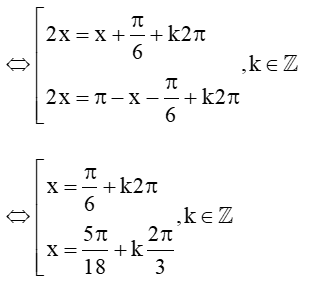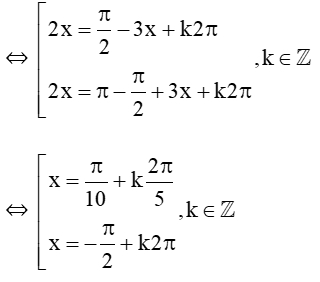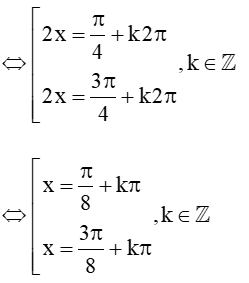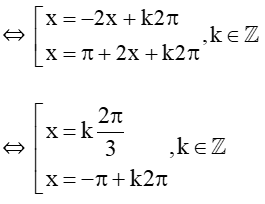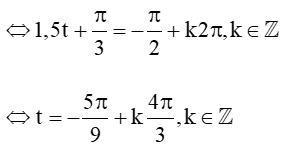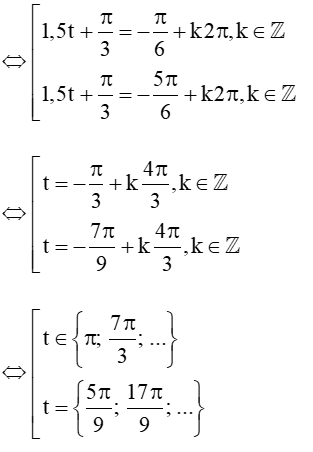Toán 11 (Chân trời sáng tạo) Bài tập cuối chương 1

Với giải bài tập Toán lớp 11 Bài tập cuối chương 1 sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 11.

1 1,725 14/08/2023

Trang trước

Trang sau

Giải Toán 11 Bài tập cuối chương 1

Giải Toán 11 trang 42 Tập 1

Bài 1 trang 42 Toán 11 Tập 1: Góc lượng giác nào tương ứng với chuyển động quay $3 \frac{1}{5}$ vòng ngược chiều kim đồng hồ?

A. $\frac{16 π}{5}$ ;

B. ${(\frac{16}{5})}^{ο}$ ;

Lời giải:

Đáp án đúng là C

Mỗi vòng kim đồng hồ quay là: 2π nên góc lượng giác quét được khi quay $3 \frac{1}{5}$ vòng là $3 \frac{1}{5} .2 π = 3.2 π + \frac{2 π}{5}$ rad.

Khi đó điểm biểu diễn cho các góc lượng giác này có công thức số đo tổng quát là $\frac{2 π}{5} + k 2 π, k \in ℤ$ .

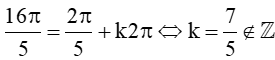
Xét Bài 1 trang 42 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11 . Do đó góc này không tương ứng với góc đã cho.

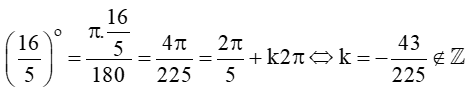
Xét Bài 1 trang 42 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11 . Do đó góc này không tương ứng với góc đã cho.

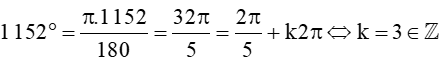
Xét Bài 1 trang 42 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11 . Do đó góc này tương ứng với góc đã cho.

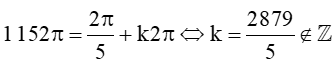
Xét Bài 1 trang 42 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11 . Do đó góc này không tương ứng với góc đã cho.

Bài 2 trang 42 Toán 11 Tập 1: Trong trường hợp nào dưới đây cosα = cosβ và sinα = – sinβ ?

A. β = – α;

B. β = π – α;

C. β = π + α;

D. $β = \frac{π}{2} + α$ .

Lời giải:

Đáp án đúng là: A

+) Xét β = – α, khi đó:

cosβ = cos(– α) = cosα;

sinβ = sin(– α) = sinα hay sinα = – sinβ .

Do đó A thỏa mãn.

+) Xét β = π – α, khi đó:

cosβ = cos(π – α) = – cosα;

sinβ = sin(π – α) = sinα.

Do đó B không thỏa mãn.

+) Xét β = π + α, khi đó:

cosβ = cos(π + α) = – cosα;

sinβ = sin(π + α) = – sinα.

Do đó C không thỏa mãn.

+) Xét $β = \frac{π}{2} + α$ , khi đó:

cosβ = cos( $\frac{π}{2} + α$ ) = – sinα;

sinβ = sin( $\frac{π}{2} + α$ ) = cosα.

Do đó D không thỏa mãn.

Bài 3 trang 42 Toán 11 Tập 1: Khẳng định nào sau đây đúng?

A. Hàm số y = sinx là hàm số chẵn;

B. Hàm số y = cosx là hàm số chẵn;

C. Hàm số y = tanx là hàm số chẵn;

D. Hàm số y = cotx là hàm số chẵn.

Lời giải:

Đáp án đúng là: B

Ta có tập xác định của hàm số y = cosx là ℝ.

Nếu với x ∈ ℝ thì – x ∈ ℝ và y(– x) = cos(– x) = cosx = y(x).

Vậy hàm số y = cosx là hàm số chẵn.

Bài 4 trang 42 Toán 11 Tập 1: Nghiệm âm lớn nhất của phương trình lượng giác cos2x = cos $(x + \frac{π}{3})$ là

A. $- \frac{π}{9}$ ;

B. $- \frac{5 π}{3}$ ;

C. $- \frac{7 π}{9}$ ;

D. $- \frac{13 π}{9}$ .

Lời giải:

Đáp án đúng là: A

cos2x = cos $(x + \frac{π}{3})$

Bài 4 trang 42 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

+) Với x = $\frac{π}{3}$ + k2 $π$ , k $\in$ Z đạt giá trị âm lớn nhất khi k = – 1 và bằng: $\frac{π}{3} - 2 π = - \frac{5 π}{3}$ .

+) Với $x = - \frac{π}{9} + k \frac{2 π}{3}, k \in ℤ$ đạt giá trị âm lớn nhất khi k = 0 và bằng: $- \frac{π}{9} + 0. \frac{2 π}{9} = - \frac{π}{9}$ .

Vậy nghiệm âm lớn nhất của phương trình đã cho là $- \frac{π}{9}$ .

Bài 5 trang 42 Toán 11 Tập 1: Số nghiệm của phương trình tanx = 3 trong khoảng $(- \frac{π}{2}; \frac{7 π}{3})$ là

Lời giải:

Xét phương trình tanx = 3

⇔ x ≈ 1,25 + kπ, k ∈ ℤ

Xét: $- \frac{π}{2} < x < \frac{7 π}{3} \Leftrightarrow - \frac{π}{2} < 1, 25 + k π < \frac{7 π}{3} \Leftrightarrow$ -0,9 < k < 1,94.

Mà k ∈ ℤ nên k ∈ {0; 1}.

Vậy có 2 nghiệm của phương trình đã cho nằm trong khoảng $(- \frac{π}{2}; \frac{7 π}{3})$ .

Bài 6 trang 42 Toán 11 Tập 1: Nhiệt độ ngoài trời ở một thành phố vào các thời điểm khác nhau trong ngày có thể được mô phỏng bởi công thức h(t) = 29 + 3sin $\frac{π}{12}$ (t-9), với h được tính bằng độ C và t là thời gian trong ngày tính bằng giờ. Nhiệt độ thấp nhất trong ngày là bao nhiêu độ C và vào lúc mấy giờ

(Theo https://www.sciencedirect.com/science/article/abs/pii/0168192385900139)

A. 32°C, lúc 15 giờ;

B. 29°C, lúc 9 giờ;

C. 26°C, lúc 3 giờ;

D. 26°C, lúc 0 giờ

Lời giải:

Vì Bài 6 trang 42 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

Bài 6 trang 42 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

Nhiệt độ thấp nhất trong ngày là 26°C khi

Bài 6 trang 42 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

Vì vậy vào thời điểm 3 giờ trong ngày thì nhiều độ thấp nhất của thành phố là 26°C.

Bài 7 trang 42 Toán 11 Tập 1: Một chiếc quạt trần năm cánh quay với tốc độ 45 vòng trong một phút. Chọn chiều quay của quạt là chiều thuận. Sau 3 giây, quạt quay được một góc có số đo bao nhiêu radian?

Lời giải:

Tốc độ góc của quạt trần là: $\frac{45.2 π}{60} = \frac{3 π}{2}$ (rad/s).

Sau 3 giây, quạt quay được một góc có số đo là: $\frac{3 π}{2} .3 = \frac{9 π}{2}$ rad.

Bài 8 trang 42 Toán 11 Tập 1: Cho cosα = $\frac{1}{3}$ và $- \frac{π}{2} < α < 0$ . Tính:

c) cos $(α + \frac{π}{3})$ .

Lời giải:

a) sinα = Bài 8 trang 42 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

b) sin2α = 2sinα.cosα = $2. \frac{1}{3} (- \frac{2 \sqrt{2}}{3}) = - \frac{4 \sqrt{2}}{9}$ .

c) Bài 8 trang 42 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

Bài 9 trang 42 Toán 11 Tập 1: Chứng minh đẳng thức lượng giác:

a) sin(α + β)sin(α – β) = sin²α – sin²β;

b) cos⁴α – cos⁴ $(α - \frac{π}{2})$ = cos2α.

Lời giải:

a) sin(α + β)sin(α – β) = sin²α – sin²β

Ta có: sin(α + β)sin(α – β) =

Bài 9 trang 42 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

Bài 9 trang 42 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

b) Ta có: cos⁴α – cos⁴ $(α - \frac{π}{2})$ = cos⁴α – sin⁴α = (cos²α – sin²α)(cos²α + sin²α)

= cos²α – sin²α = cos2α.

Giải Toán 11 trang 43 Tập 1

Bài 10 trang 43 Toán 11 Tập 1: Nghiệm dương nhỏ nhất của phương trình sin $(x + \frac{π}{6})$ - sin2x = 0 là bao nhiêu?

Lời giải:

Xét phương trình sin $(x + \frac{π}{6})$ - sin2x = 0

$\Leftrightarrow$ sin2x = sin $(x + \frac{π}{6})$

Bài 10 trang 43 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

Với họ nghiệm $x = \frac{π}{6} + k 2 π$ có nghiệm dương bé nhất là $x = \frac{π}{6}$ khi k = 0.

Với họ nghiệm $x = \frac{5 π}{18} + k \frac{2 π}{3}$ có nghiệm dương bé nhất là $x = \frac{5 π}{18}$ khi k = 0.

Vậy nghiệm dương bé nhất của phương trình đã cho là $x = \frac{π}{6}$ .

Bài 11 trang 43 Toán 11 Tập 1: Giải các phương trình sau:

a) sin2x + cos3x = 0;

b) sinxcosx = $\frac{\sqrt{2}}{4}$ ;

c) sinx + sin2x = 0.

Lời giải:

a) sin2x + cos3x = 0

⇔ sin2x = sin $(\frac{π}{2} - 3 x)$

Bài 11 trang 43 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

Vậy phương trình có tập nghiệm là S = $(\frac{π}{10} + k \frac{2 π}{5}; - \frac{π}{2} + k 2 π, k \in ℤ)$ .

b) sinxcosx = $\frac{\sqrt{2}}{4}$

$\Leftrightarrow$ sin2x = $\frac{\sqrt{2}}{2}$

$\Leftrightarrow$ sin2x = sin $\frac{π}{4}$

Bài 11 trang 43 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

Vậy tập nghiệm của phương trình là S = $(\frac{π}{8} + k π; \frac{3 π}{8} + k π, k \in ℤ)$ .

c) sinx + sin2x = 0.

⇔ sinx = – sin2x

⇔ sinx = sin(– 2x)

Bài 11 trang 43 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

Vậy tập nghiệm của phương trình là: S = $(k \frac{2 π}{3}; - π + k 2 π, k \in ℤ)$ .

Bài 12 trang 43 Toán 11 Tập 1: Độ sâu h(m) của mực nước ở một cảng biển vào thời điểm t (giờ) sau khi thủy triều lên lần đầu tiên trong ngày được tính xấp xỉ bởi công thức h(t) = 0,8cos0,5t + 4.

(Theo https://noc.ac.uk/files/documents/business/an-introduction-to-tidal-modelling.pdf)

a) Độ sâu của nước vào thời điểm t = 2 là bao nhiêu mét?

b) Một con tàu cần mực nước sâu tối thiểu 3,6m để có thể di chuyển vào cảng an toàn. Dựa vào đồ thị của hàm số côsin, hãy cho biết trong vòng 12 tiếng sau khi thủy triều lên lần đầu tiên, ở những thời điểm t nào tàu có thể hạ thủy. Làm tròn kết quả đến hàng phần trăm.

Lời giải:

a) Tại thời điểm t = 2 độ sâu của nước là: h(2) = 0,8cos0,5.2 + 4 ≈ 4,43 m.

Vậy độ sâu của nước ở thời điểm t = 2 là khoảng 4,43 m.

b) Các thời điểm để mực nước sâu là 3,6m tương ứng với phương trình 0,8cos0,5t + 4 = 3,6

⇔ 0,8cos0,5t = – 0,4

⇔ cos0,5t = – 0,5

⇔ cos0,5t = cos $\frac{2 π}{3}$

⇔ 0,5t = $\pm \frac{2 π}{3} + k 2 π, k \in ℤ$

⇔ t = $\pm \frac{4 π}{3} + k 2 π, k \in ℤ$

+) Với $t = \frac{4 π}{3} + k 2 π, k \in ℤ$ , trong 12 tiếng ta có các thời điểm

$0 \leq \frac{4 π}{3} + k 2 π \leq 12 \Leftrightarrow - \frac{2}{3} \leq k \leq 1, 24$

Mà $k \in ℤ$ nên k $\in$ {0;1}.

+) Với $t = - \frac{4 π}{3} + k 2 π, k \in ℤ$ , trong 12 tiếng ta có các thời điểm

$0 \leq - \frac{4 π}{3} + k 2 π \leq 12 \Leftrightarrow \frac{2}{3} \leq k \leq 1, 24$

Mà k $\in$ Z nên k=1.

Vậy tại các thời điểm $t = \frac{4 π}{3}, t = \frac{10 π}{3}, t = \frac{2 π}{3}$ giờ thì tàu có thể hạ thủy.

Bài 13 trang 43 Toán 11 Tập 1: Cho vận tốc v (cm/s) của một con lắc đơn theo thời gian t (giây) được cho bởi công thức v = -3sin $(1, 5 t + \frac{π}{3})$ .

(Theo https://www.britannica.com/science/simple-harmonic-motion)

Xác định các thời điểm t mà tại đó:

a) Vận tốc con lắc đạt giá trị lớn nhất;

b) Vận tốc con lắc bằng 1,5 cm/s.

Lời giải:

a) Vì $- 1 \leq \sin (1, 5 t + \frac{π}{3}) \leq 1$ nên $- 3 \leq - 3 \sin (1, 5 t + \frac{π}{3}) \leq 3$

Vận tốc con lắc đạt giá trị lớn nhất khi sin $(1, 5 t + \frac{π}{3})$ = -1

Bài 13 trang 43 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

Vì vậy vận tốc con lắc đạt giá trị lớn nhất tại các thời điểm $t_{1} = \frac{7 π}{9}; t_{2} = \frac{19 π}{9}; t_{3} = \frac{31 π}{9}; ...$

b) Để vận tốc con lắc bằng 1,5 cm/s thì v = -3sin $(1, 5 t + \frac{π}{3})$ = 1,5

$\Leftrightarrow \sin (1, 5 t + \frac{π}{3}) = - \frac{1}{2}$

Dựa vào đồ thị hàm số sin ta có:

Bài 13 trang 43 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

Vậy sau các thời điểm $t_{1} = \frac{5 π}{9}, t_{2} = π, t_{3} = \frac{17 π}{9}, t_{4} = \frac{7 π}{3}, ...$ thì vận tốc của con lắc đạt 1,5 cm/s.

Bài 14 trang 43 Toán 11 Tập 1: Trong Hình 1, cây xanh AB nằm ở trên đường xích đạo được trồng vuông góc với mặt đất và có chiều cao 5m. Bóng của cây là BE. Vào nghày xuân phân và hạ phân, điểm E di chuyển trên đường thẳng Bx. Góc thiên đỉnh θ_s = (AB, AE) phụ thuộc vào vị trí của Mặt Trời và thay đổi theo thời gian trong ngày theo công thức θ_s(t) = $\frac{π}{12} (t - 12)$ rad với t là thời gian trong ngày (theo đơn vị giờ, 6 < t < 18) .

(Theo https://www.sciencedirect.com/topics/engineering/solar-hour-angle)

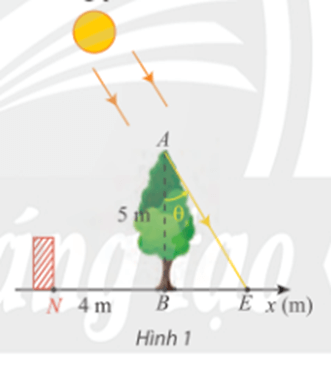
a) Viết hàm số biểu diễn tọa độ của điểm E trên trục Bx theo t.

b) Dựa vào đồ thị của hàm số tang, hãy xác định các thời điểm mà tại đó bóng cây phủ qua vị trí tường rào N biết N nằm trên trục Bx với tọa độ x_N = – 4 (m). Làm tròn kết quả đến hàng phần mười.

Lời giải:

a) Xét tam giác ABE vuông tại B, có:

$\tan θ_{s} (t) = \frac{B E}{A B} \Leftrightarrow B E = 5 \tan (\frac{π}{12} (t - 12))$ .

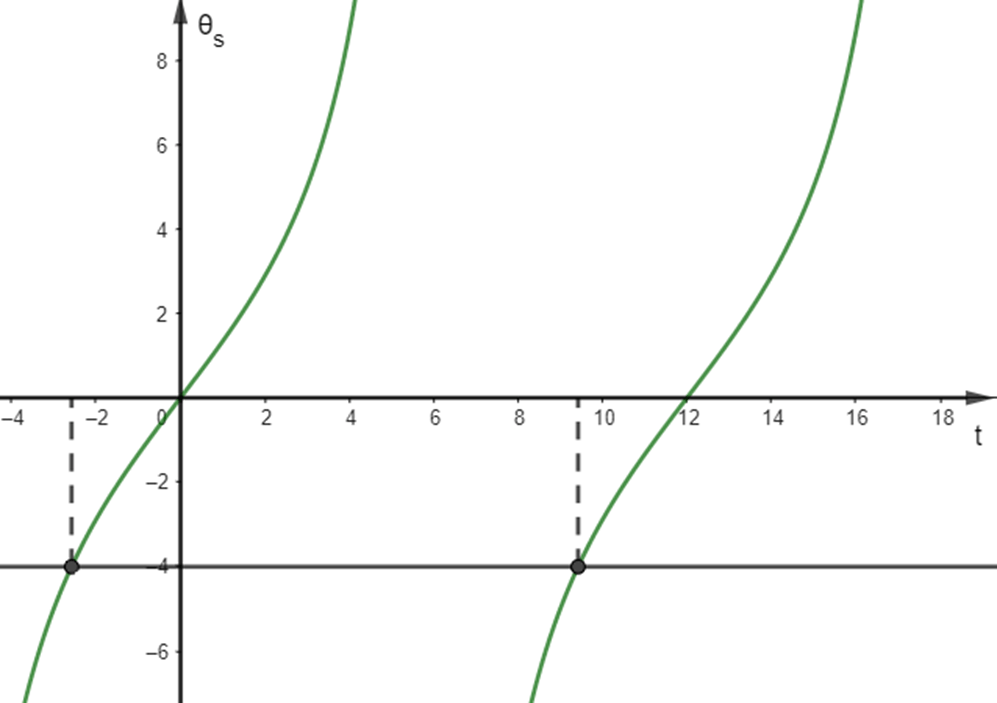
b) Đồ thị của hàm số $θ_{s} = 5 \tan (\frac{π}{12} (t - 12))$

Bài 14 trang 43 Toán 11 Tập 1 Chân trời sáng tạo | Giải Toán 11

Dựa vào đồ thị hàm số để $θ_{s} = 5 \tan (\frac{π}{12} (t - 12)) < - 4$ và 6 < t < 18 suy ra các thời điểm để bóng cây phủ qua hàng rào N là 6 < t< 9,4.

Xem thêm lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Góc lượng giác

Bài 2: Giá trị lượng giác của một góc lượng giác

Bài 3: Các công thức lượng giác

Bài 5: Phương trình lượng giác

Bài tập cuối chương 1

1 1,725 14/08/2023

Trang trước

Trang sau

Xem thêm các chương trình khác: