Giải Toán 10 trang 102 Tập 2 Cánh diều
Với giải bài tập Toán lớp 10 trang 102 Tập 2 trong Bài 6: Ba đường conic sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 trang 102 Tập 2.
Giải Toán 10 trang 102 Tập 2
Bài 1 trang 102 Toán 10 Tập 2: Phương trình nào sau đây là phương trình chính tắc của elip?
Lời giải
Phương trình chính tắc của elip có dạng với a > b > 0.
+ Đáp án a, ta thấy a2 = b2 = 64, không thỏa mãn điều kiện a > b > 0.
+ Đáp án b, không phải dạng của phương trình chính tắc của elip.
+ Đáp án c, ta có a2 = 64, b2 = 25, suy ra a = 8, b = 5 nên a > b > 0, thỏa mãn.
+ Đáp án d, ta thấy a2 = 25, b2 = 64, suy ra a = 5 và b = 8 nên a < b, không thỏa mãn.
Vậy trong các phương trình đã cho thì phương trình c) là phương trình chính tắc của elip.
Bài 2 trang 102 Toán 10 Tập 2: Cho elip (E) có phương trình chính tắc Tìm tọa độ các giao điểm của (E) với trục Ox, Oy và tọa độ các tiêu điểm của (E).
Lời giải
Ta có:
+ Trục hoành Ox: y = 0, tọa độ giao điểm của (E) với trục hoành là nghiệm của hệ
.
Giải hệ trên ta được 2 nghiệm (7; 0) và (– 7; 0).
Vậy tọa độ các giao điểm của (E) với trục Ox là A1(– 7; 0), A2(7; 0).
+ Trục tung Oy: x = 0, tọa độ giao điểm của (E) với trục tung là nghiệm của hệ
.
Giải hệ trên ta được 2 nghiệm là (0; – 5), (0; 5).
Vậy tọa độ các giao điểm của (E) với trục Oy là B1(0; – 5), B2(0; 5).
+ Ta có:
Vì a > b > 0 nên elip (E) có a = 7, b = 5.
Suy ra c2 = a2 – b2 = 72 – 52 = 24.
Do đó, .
Vậy tọa độ các tiêu điểm của (E) là .
Bài 3 trang 102 Toán 10 Tập 2: Viết phương trình chính tắc của elip (E), biết tọa độ hai giao điểm của (E) với Ox và Oy lần lượt là A1(– 5; 0) và B2(0; ).
Lời giải
Phương trình chính tắc của elip (E) có dạng với a > b > 0.
+ Elip (E) cắt trục Ox tại A1(– 5; 0) nên .
Do a > 0 nên a = 5.
+ Elip (E) cắt trục Oy tại nên
Do b > 0 nên .
Vì 5 > nên a > b > 0 (thỏa mãn).
Vậy phương trình chính tắc của elip (E) là .
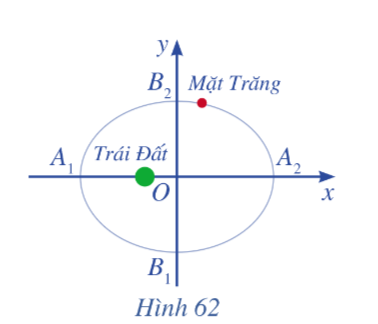
Bài 4 trang 102 Toán 10 Tập 2: Ta biết rằng Mặt Trăng chuyển động quanh Trái Đất theo quỹ đạo là một elip mà Trái Đất là một tiêu điểm. Elip đó có A1A2 = 768 800 km và B1B2 = 767 619 km (Nguồn: Ron Larson (2014), Precalculus Real Mathematics, Real People, Cengage) (Hình 62). Viết phương trình chính tắc của elip đó.
Lời giải
Phương trình chính tắc của elip cần lập có dạng với a > b > 0.
+ Trục Oy là đường trung trực của đoạn A1A2 nên O là trung điểm của A1A2
Suy ra OA2 = .
Vì điểm A2 nằm trên trục Ox về phía bên phải điểm O nên A2(384 800; 0).
Điểm A2 thuộc elip (E) nên
(do a > 0).
+ Trục Ox là đường trung trực của đoạn B1B2 nên O là trung điểm của B1B2
Suy ra OB2 = .
Vì điểm B2 nằm trên trục Oy về phía bên trên điểm O nên B2(0; 383 809,5).
Elip (E) cắt trục Oy tại B2(0; 338309,5), thay vào phương trình elip ta được:
(do b > 0).
Do 384 800 > 383 809,5 nên a > b > 0 (thỏa mãn).
Vậy phương trình chính tắc của elip (E) là .
Bài 5 trang 102 Toán 10 Tập 2: Những phương trình nào sau đây là phương trình chính tắc của hypebol?
Lời giải
Phương trình chính tắc của hypebol có dạng với a > 0, b > 0.
+ Phương trình ở đáp án a không có dạng trên nên đây không phải phương trình chính tắc của hypebol.
+ Các phương trình ở các đáp án b, c, d đều là phương trình chính tắc của hypebol vì đều có dạng trên và thỏa mãn điều kiện a > 0, b > 0. Cụ thể
- Đáp án b: a = b = 3 > 0.
- Đáp án c: a = 3 > 0, b = 8 > 0.
- Đáp án d: a = 8 > 0, b = 3 > 0.
Vậy các phương trình ở đáp án b, c, d là phương trình chính tắc của hypebol.
Bài 6 trang 102 Toán 10 Tập 2: Tìm tọa độ các tiêu điểm của đường hypebol trong mỗi trường hợp sau:
Lời giải
a) Ta có: .
Suy ra hypebol có a2 = 9, b2 = 16.
Do đó, c2 = a2 + b2 = 9 + 16 = 25.
Từ đó suy ra c = 5.
Vậy tọa độ các tiêu điểm của hypebol đã cho là F1(– 5; 0) và F2(5; 0).
b) Ta có:
Suy ra hypebol có a2 = 36, b2 = 25.
Do đó, c2 = a2 + b2 = 36 + 25 = 61
Từ đó suy ra .
Vậy tọa độ các tiêu điểm của hypebol đã cho là F1(–; 0) và F2(; 0).
Bài 7 trang 102 Toán 10 Tập 2: Viết phương trình chính tắc của hypebol (H), biết nằm trên (H) và hoành độ một giao điểm của (H) đối với trục Ox bằng 3.
Lời giải
Gọi dạng của phương trình chính tắc của hypebol (H) là với a > 0, b > 0.
+ Hoành độ một giao điểm của (H) với trục Ox là 3 nên tọa độ giao điểm của (H) với trục Ox là điểm (3; 0). Khi đó ta có:
(do a > 0).
+ Điểm nên (do b > 0).
Vậy phương trình chính tắc của hypebol (H) là .
Bài 8 trang 102 Toán 10 Tập 2: Những phương trình nào sau đây là phương trình chính tắc của parabol?
Lời giải
Phương trình chính tắc của parabol có dạng y2 = 2px (với p > 0).
a) y2 = – 2x = 2 . (– 1)x, vì (– 1) < 0 nên đây không phải phương trình chính tắc của parabol.
b) y2 = 2x = 2 . 1 . x, vì 1 > 0 nên đây là phương trình chính tắc của parabol với p = 1.
c) Phương trình x2 = – 2y không có dạng phương trình chính tắc của parabol nên đây không phải là phương trình chính tắc của parabol.
d) Ta có: , vì nên đây là phương trình chính tắc của parabol với .
Vậy trong các đáp án đã cho thì phương trình ở đáp án b và d là phương trình chính tắc của parabol.
Bài 9 trang 102 Toán 10 Tập 2: Tìm tọa độ tiêu điểm và viết phương trình đường chuẩn của đường parabol trong mỗi trường hợp sau:
Lời giải
a) Ta có: .
Suy ra parabol có p = (thỏa mãn p > 0).
Ta có: .
Vậy tọa độ tiêu điểm của parabol này là và phương trình đường chuẩn là .
b) Ta có: .
Suy ra parabol có p = (thỏa mãn p > 0).
Ta có: .
Vậy tọa độ tiêu điểm của parabol này là và phương trình đường chuẩn là .
Bài 10 trang 102 Toán 10 Tập 2: Viết phương trình chính tắc của đường parabol, biết tiêu điểm là F(6; 0).
Lời giải
Gọi dạng của phương trình chính tắc của parabol là y2 = 2px (với p > 0).
Vì tiêu điểm của parabol là F(6; 0). Suy ra .
Vậy phương trình chính tắc của parabol là y2 = 2 . 12 x hay y2 = 24x.
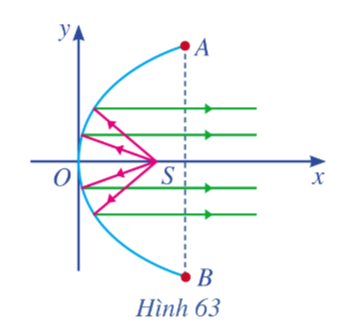
Bài 11 trang 102 Toán 10 Tập 2: Một chiếc đèn có mặt cắt ngang là hình parabol (Hình 63). Hình parabol có chiều rộng giữa hai mép vành là AB = 40 cm và chiều sâu h = 30 cm (h bằng khoảng cách từ O đến AB). Bóng đèn nằm ở tiêu điểm S. Viết phương trình chính tắc của parabol đó.
Lời giải
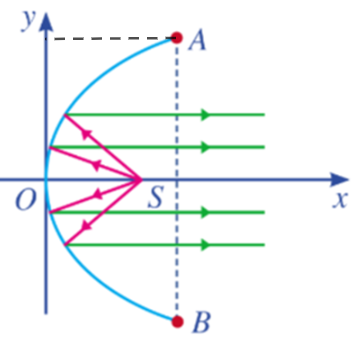
Do AB = 40 và Ox là đường trung trực của đoạn AB.
Suy ra khoảng cách từ điểm A đến trục Ox là . (1)
Chiều sâu h bằng khoảng cách từ O đến AB và h = 30.
Suy ra khoảng cách từ điểm A đến trục Oy là 30. (2)
Từ (1) và (2) suy ra, parabol đi qua điểm A(30; 20).
Phương trình chính tắc của parabol có dạng y2 = 2px (với p > 0).
Khi đó ta có: 202 = 2p . 30 ⇔ 60p = 400 ⇔ p = (thỏa mãn p > 0).
Vậy phương trình chính tắc của parabol thỏa mãn bài toán là .
Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:
Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:
Chủ đề 2: Xây dựng mô hình hàm số bậc nhất, bậc hai biểu diễn số liệu dạng bảng
Xem thêm các chương trình khác:
- Soạn văn lớp 10 (hay nhất) – Cánh Diều
- Tác giả tác phẩm Ngữ văn lớp 10 – Cánh Diều
- Tóm tắt tác phẩm Ngữ văn lớp 10 – Cánh Diều
- Bố cục tác phẩm Ngữ văn lớp 10 – Cánh Diều
- Nội dung chính tác phẩm Ngữ văn lớp 10 – Cánh Diều
- Soạn văn lớp 10 (ngắn nhất) – Cánh Diều
- Giải sbt Ngữ văn lớp 10 – Cánh Diều
- Văn mẫu lớp 10 – Cánh Diều
- Giải Chuyên đề học tập Ngữ văn 10 – Cánh diều
- Giải sgk Tiếng Anh 10 – Explore new worlds
- Giải sgk Tiếng Anh 10 – ilearn Smart World
- Trọn bộ Từ vựng Tiếng Anh 10 ilearn Smart World đầy đủ nhất
- Ngữ pháp Tiếng Anh 10 i-learn Smart World
- Giải sbt Tiếng Anh 10 - iLearn Smart World
- Giải sgk Vật lí 10 – Cánh Diều
- Giải sbt Vật lí 10 – Cánh Diều
- Lý thuyết Vật lí 10 – Cánh Diều
- Giải Chuyên đề Vật lí 10 – Cánh Diều
- Giải sgk Hóa học 10 – Cánh Diều
- Lý thuyết Hóa học 10 – Cánh Diều
- Giải sbt Hóa học 10 – Cánh Diều
- Giải Chuyên đề Hóa học 10 – Cánh Diều
- Giải sgk Sinh học 10 – Cánh Diều
- Giải sbt Sinh học 10 – Cánh Diều
- Lý thuyết Sinh học 10 – Cánh Diều
- Giải Chuyên đề Sinh học 10 – Cánh diều
- Giải sgk Lịch sử 10 – Cánh Diều
- Giải sbt Lịch sử 10 – Cánh Diều
- Giải Chuyên đề Lịch sử 10 – Cánh Diều
- Lý thuyết Lịch sử 10 – Cánh diều
- Giải sgk Địa lí 10 – Cánh Diều
- Lý thuyết Địa Lí 10 – Cánh Diều
- Giải sbt Địa lí 10 – Cánh Diều
- Giải Chuyên đề Địa lí 10 – Cánh Diều
- Lý thuyết Công nghệ 10 – Cánh Diều
- Giải sgk Công nghệ 10 – Cánh Diều
- Giải sgk Giáo dục Kinh tế và Pháp luật 10 – Cánh Diều
- Giải sbt Giáo dục Kinh tế và Pháp luật 10 – Cánh Diều
- Giải Chuyên đề Kinh tế pháp luật 10 – Cánh diều
- Lý thuyết KTPL 10 – Cánh diều
- Lý thuyết Giáo dục quốc phòng 10 – Cánh Diều
- Giải sgk Giáo dục quốc phòng - an ninh 10 – Cánh diều
- Giải sbt Giáo dục quốc phòng - an ninh 10 – Cánh Diều
- Giải sgk Hoạt động trải nghiệm 10 – Cánh Diều
- Giải sbt Hoạt động trải nghiệm 10 – Cánh Diều
- Giải sgk Tin học 10 – Cánh Diều
- Giải sbt Tin học 10 – Cánh Diều
- Giải Chuyên đề Tin học 10 – Cánh diều
- Lý thuyết Tin học 10 - Cánh diều
- Giải sgk Giáo dục thể chất 10 – Cánh Diều